Булевы функции одной и двух переменных
Перечислим без дальнейших пояснений 4 логические функции одной переменной и 16 логических функций двух переменных (табл. 3, табл. 4, табл. 5, табл.6).
Таблица 3
| x | f1 | f2 | f3 | f4 |
Таблица 4
| Функция | Название | Обозначение | Фиктивная переменная |
| f1 | Ноль (противоречие) | x | |
| f2 | Тождественная | x | |
| f3 | Отрицание | 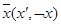 | |
| f4 | Единица (тавтология) | x |
Таблица 5
| x1 | x2 | f1 | f2 | f3 | f4 | f5 | f6 | f7 | f8 | f9 | f10 | f11 | f12 | f13 | f14 | f15 | f16 |
Таблица 6
| Функция | Название | Обозначение | Фиктивная переменная |
| f1 | Ноль (противоречие) | x1, x2 | |
| f2 | Логическое умножение; конъюнкция; и | 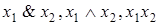 | - |
| f3 | - | - | - |
| f4 | - | 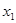 | x2 |
| f5 | - | - | - |
| f6 | - | 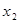 | x1 |
| f7 | Сложение по модулю 2 | 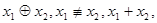 x1∆x2 x1∆x2 | - |
| f8 | Логическое сложение; дизъюнкция; или | 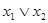 | - |
| Окончание табл. 6 | |||
| f9 | Стрелка Пирса | 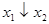 | - |
| f10 | Эквивалентность | x1~x2, 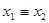 | - |
| f11 | - | 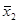 | x1 |
| f12 | - | - | - |
| f13 | - | 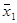 | x2 |
| f14 | Импликация; если, то | 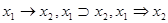 | - |
| f15 | Штрих Шеффера | x1|x2 | - |
| f16 | Единица (тавтология) | x1, x2 |
Отметим, что в импликации 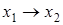 переменная
переменная 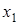 называется посылкой, а переменная
называется посылкой, а переменная 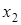 − заключениемимпликации. Импликация ложна в одном единственном случае, когда посылка истинна, а заключение ложно. Логики говорят, что из истины не может следовать ложь, а из лжи может следовать что угодно.
− заключениемимпликации. Импликация ложна в одном единственном случае, когда посылка истинна, а заключение ложно. Логики говорят, что из истины не может следовать ложь, а из лжи может следовать что угодно.
Формулы
Символы логических операций 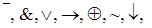 | назовем логическими связками. Формула - это последовательность имен переменных, соединенных логическими связками, и составленная по определенным правилам. Формула может содержать также открывающие и закрывающие скобки. Связки
| назовем логическими связками. Формула - это последовательность имен переменных, соединенных логическими связками, и составленная по определенным правилам. Формула может содержать также открывающие и закрывающие скобки. Связки 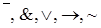 назовем основными.
назовем основными.
Перечислим правила построения формул.
1. Всякая переменная, быть может с индексами, - это формула. Логические константы 0 и 1 - это формулы.
2. Если 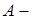 формула, то
формула, то 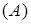 и
и 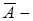 это формулы.
это формулы.
3. Если 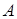 и
и 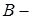 формулы, то
формулы, то 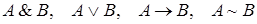 ,
, 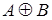 ,
, 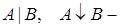 это формулы.
это формулы.
4. Других формул нет.
Пример. Последовательности символов 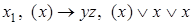 - это формулы. Последовательность
- это формулы. Последовательность 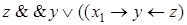 формулой не является.
формулой не является.
Всякая формула определяет некоторую логическую функцию, по-другому говорят, что формула реализует некоторую логическую функцию. За каждой формулой скрыта таблица истинности. Поэтому нужно уметь вычислять значение формулы во всякой строке таблицы истинности, на всяком наборе значений ее аргументов. Порядок вычисления значения формулы определяется скобками. Если скобок нет, значение формулы вычисляется слева направо в соответствии со старшинством операций. Иерархия операций (в порядке убывания старшинства) задается так:  ,(&, |, ↓),
,(&, |, ↓), 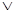 , →, (~,
, →, (~, 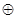 ). В скобках указаны равносильные операции.
). В скобках указаны равносильные операции.
Определение. Формулы, реализующие одну и ту же функцию, называются равносильными. Значит, у равносильных формул совпадают таблицы истинности».
Утверждение. Каковы бы ни были формулы x, y, z справедливы следующие равносильности
1. x 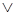 x = x; x&x = x (идемпотентность);
x = x; x&x = x (идемпотентность);
2. x 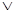 y = y
y = y 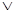 x; x&y = y&x (коммутативность);
x; x&y = y&x (коммутативность);
3. x 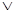 (y
(y 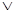 z) = (x
z) = (x 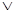 y)
y) 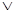 z; x&(y&z) = (x&y)&z (ассоциативность);
z; x&(y&z) = (x&y)&z (ассоциативность);
4. (x&y) 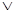 x = x; (x
x = x; (x 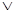 y)&x = x (законы поглощения);
y)&x = x (законы поглощения);
5. x 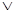 (y&z) = (x
(y&z) = (x 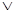 y)&(x
y)&(x 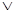 z); x&(y
z); x&(y 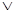 z) = (x&y)
z) = (x&y) 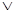 (x&z) (законы дистрибутивности);
(x&z) (законы дистрибутивности);
6. x 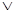 1 = 1; x&1 = x (свойства единицы);
1 = 1; x&1 = x (свойства единицы);
7. x 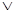 0 = x; x&0 = 0 (свойства нуля);
0 = x; x&0 = 0 (свойства нуля);
8. 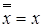 (инволютивность);
(инволютивность);
9. 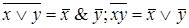 (законы де Моргана);
(законы де Моргана);
10. 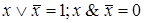 (свойства дополнения).
(свойства дополнения).
Замечание. Для упрощения обозначений символ коньюнкции & часто опускается, вместо x&y пишут просто xy.
Другие полезные равносильности:
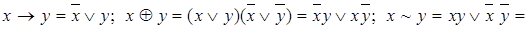
= 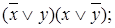
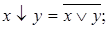 x|y =
x|y = 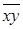 .
.
Доказательство проводится построением соответствующих таблиц истинности.
