Приклад чисельного розрахунку мішаного з’єднання споживачів символічним способом.

Надання опорів ділянок у вигляді комплексів, Ом:

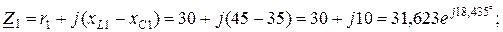
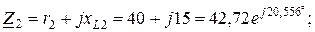
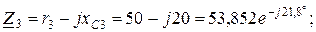
дає підстави привести розрахункову схему (рис. 2.27, а) до виду рис. 2.27, б. Далі, з метою спрощення схеми до виду, як на рис. 2.27, в, опори Z₂ та Z₃ паралельних ділянок замінюють еквівалентним опором, Ом:

;

.

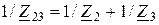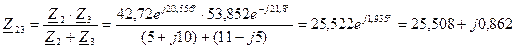Заміна двох, ввімкнених послідовно, опорів, Z₁ і Z₂₃ еквівалентним, Ом:

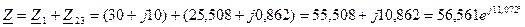
дає підстави привести розрахункову схему до виду як рис. 2.27, г.

За умовою задачі розрахунок виконується на момент, коли синусоїда напруги джерела проходить через початок системи координат u(wt), тобто вектор 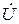спрямований по осі дійсних чисел комплексної площини. Отже, комплекс напруги джерела буде, В:

.

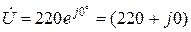У випадку, коли за умовою задано діюче значення напруги джерела, момент часу, для якого виконується розрахунок, може бути обраний довільно. Разом з тим, з метою зручності, виконання аналізу кола частіше обирають момент, коли у системі u = f(wt) синусоїда напруги джерела проходить саме через початок координат.

За законом Ома комплекс струму кола – він же комплекс струму на першій ділянці з’єднання, буде, А:

.

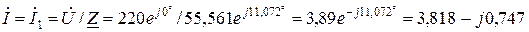Комплекси спадів напруги на ділянках кола, В:

,

.

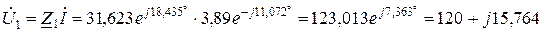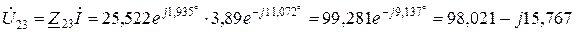Точність обчислення спадів напруги на ділянках кола перевіряють за другим законом Кірхгофа:

,

.

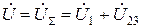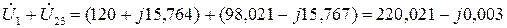З результатів порівняння маємо:

,

.

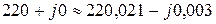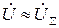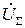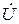Якщо відносні розбіжності активних і реактивної складових та не перебільшують обумовленої заздалегідь похибки, то розрахунок можна продовжувати далі. У протилежному випадку, необхідно зробити перевірку попередньо виконаних обчислень.

Комплекси струмів у паралельних вітках, А:

;

.

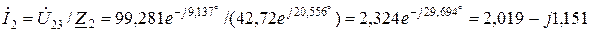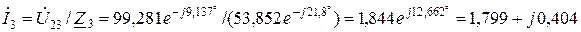Точність обчислення струмів ділянок кола перевіряють за першим законом Кірхгофа:

;

;

,

.

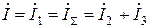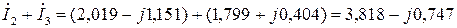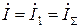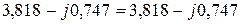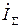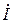Якщо відносні розбіжності активних і реактивної складових та не перебільшують обумовленої заздалегідь похибки, то розрахунок можна продовжувати далі. У протилежному випадку, необхідно зробити перевірку попередньо виконаних обчислень.

Кути зсуву фаз між струмом і напругою на ділянках кола, °:

;

;

;

;

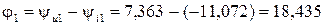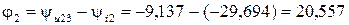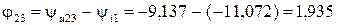і всього кола, ° –

.

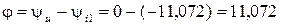Точність розрахунку перевіряють шляхом порівняння потужностей споживача і джерела. Комплекс повної потужності джерела розраховують за формулою, В×А:

.

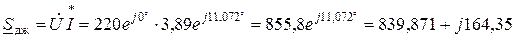Оскільки S_дж = P_дж + jQ_дж, то: P_дж = 839,871 Вт, а Q_дж = 164,35 вар.

Комплекси повної потужності споживача, В×А:

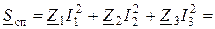
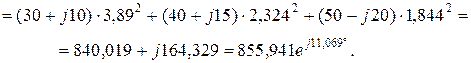
Звідси: P_сп = 840,019 Вт, а Q_сп = 164,329 вар.

Якщо відносні розбіжності результатів розрахунку активних d_P та реактивних d_Q потужностей споживача і джерела не перебільшують обумовленої заздалегідь похибки, то розрахунок вважають виконаним вірно. У даному випадку похибки складають, %:

;

.

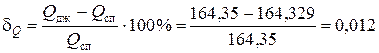За результатами розрахунку на комплексній площині будують суміщену векторну діаграму струмів та напруг кола (рис. 2.28, б). Для цього спочатку обирають зручні масштаби побудови векторів струму М_і (А/мм,) і напруги М_u (В/мм). Порядок побудови векторної діаграми такий:

1. Вектор 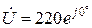– з початку координат, по осі дійсних чисел (y_u = 0^°) відкладають відрізок довжиною 220/М_u ;

2. Вектор 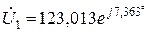– з початку координат, під кутом y_u1 = 7,363^° до осі дійсних чисел відкладають відрізок довжиною 123,013/М_u;

3. Вектор 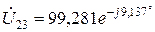– з кінця вектору 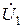під кутом y_u23 = - 9,137^° до осі дійсних чисел відкладають відрізок довжиною 99,281/ М_u;

4. Вектор 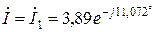– з початку координат, під кутом y_і = y_і1= - 11,072^° до осі дійсних чисел відкладають відрізок довжиною 3,89/М_і;

5. Вектор 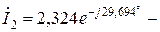з початку координат, під кутом y_і2 = – 29,694^° до осі дійсних чисел відкладають відрізок довжиною 2,324/М_і;

6. Вектор 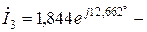з початку координат, під кутом y_і3 = 12,662^° до осі дійсних чисел відкладають відрізок довжиною 1,844/М_і.

Якщо на векторній діаграмі вектори 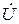, 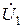і 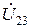утворюють трикутник напруг, а вектори 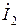та 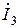є сторонами паралелограму, діагональ якого 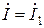то розрахунок виконано правильно. Між векторами струмів і відповідними векторами напруг показують кути зсуву фаз на ділянках кола.

Питання для самоперевірки та модульного контролю за розділом

1. Який фізичний зміст мають поняття: резистор, індуктивність, електрична ємність?

2. Що називають електричним колом (ділянкою, вузлом, віткою, контуром електричного кола)?

3. Яке електричне коло називають лінійним (нелінійним)?

4. Якій стум називають синусоїдним?

5. Які основні переваги має синусоїдний струм у порівнянні з постійним електричним струмом?

6. Що називають періодом (частотою) синусоїдної величини?

7. Що називають фазою (початковою фазою) синусоїдної електричної величини?

8. Що називають миттєвим значенням синусоїдної електричної величини?

9. Які синусоїдні електричні величини називають такими, що співпадають (зсунутими) між собою за фазою?

10. Що називають фазовим кутом?

11. Що називають кутом зсуву фаз?

12. Що називають векторною діаграмою електричних величин?

13. Що називають діючим значенням синусоїдної електричної величини?

14. Що називають середнім значенням синусоїдної електричної величини?

15. Якими приладами вимірюють миттєві значення електричного струму і напруги?

16. Якими приладами вимірюють діючі значення електричного струму і напруги?

17. В чому полягає відмінність активного та реактивного опорів?

18. В чому полягає відмінність закону Ома для кіл постійного і змінного струмів?

19. Як формулюється перший закон Кірхгофа для кіл постійного і змінного струмів?

20. Як формулюється другий закон Кірхгофа для кіл постійного і змінного струмів?

21. Чому дорівнює кут зсуву фаз між струмом і напругою на ділянці кола з резистором (індуктивністю, електричною ємністю)?

22. Які еквівалентні трикутники електричних величин Ви знаєте?

23. В чому полягає фізичний зміст cosj?

24. В яких одиницях вимірюють активну, реактивну та повну електричні потужності?

25. Яке з’єднання електричних елементів (ділянок кола) називають послідовним (паралельним)?

26. Яке з’єднання електричних елементів (ділянок кола) називають паралельним?

27. Яке з’єднання електричних елементів (ділянок кола) називають мішаним?