Основные позиции закона РФ «Об обеспечении единства измерений» от 26.06.2008 № 102 – ФЗ. 4 страница

Относительная погрешность измерения -по­грешность измерения,выраженная отношением абсолютной погреш­ности измерения кдействительному или измеренному значению из­меряемой величины.

Относительную погрешность в долях или процентах находят изотношений

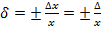или в процентах 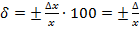∙100,

где Δх = Δ - абсолютная погрешность измерений.

Приведенная погрешность СИ γ - относительная погрешность, выраженная отношением абсолютной погрешности средстваизмерений Δ_СИ к условно принятому значению величины Х_N ,постоянному во всем диапазоне измерений или в части диапазона

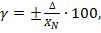
где γ - приведенная погрешность, %;

Х_N – нормирующее значение ФВ.

Часто за нормирующее значение принимают верх­ний пределизмерений или сумму значений шкал при двусторонней шкале.

Примервыражения результатов измерения в единицах измеряемой ФВ при отсчете по шкалам приборов, на которых указана относительная или приведенная погрешности.

Отсчет по шкале прибора с пределами измерений 0 – 50 А и равномерной шкалой составил 25 А. Пренебрегая другими видами погрешности измерения, оценить пределы допускаемой абсолютной погрешности этого отсчета при использовании различных СИ класса точности:

0,02 / 0,01; 0,5 и 0,5.

Решение.1.Для СИ класса точности 0,02 / 0,01 δ = Δ/х = ± [c + d (| x_к / х| - 1)].

Так как х = 25, x_к = 50, с = 0,02, d = 0,01 и δ дано в процентах, то

δ = ± [0,02 + 0,01(| 50 / 25| - 1)] = ± 0,03%; Δ = ± δ∙ х/100 = ±( 0,03∙25/100) = ± 0,0075 А.

2. Для СИ класса точности 0,5

δ = ± Δ / х; Δ = ± 0,01∙ δ∙ х = ± 0,01∙0,5∙25 = ± 0,125 А.

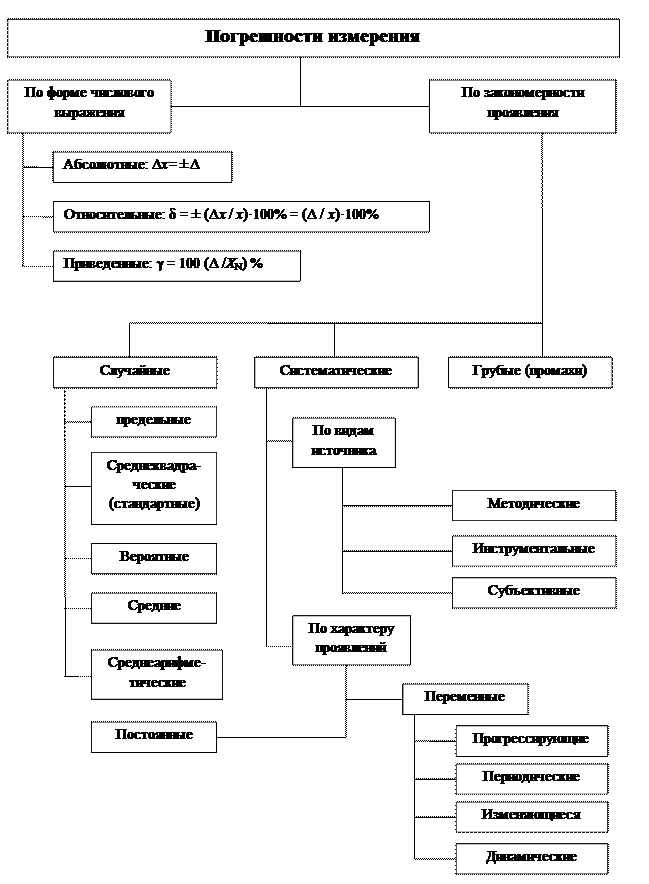
Рисунок 5 - Классификация погрешностей измерений

3. Для СИ класса точности 0,5

γ = ± (Δ / х_N), где х_N = 50, тогда Δ = ± 0,01∙50∙0,5 = 0,25 А.

1.13. Погрешность измерений. Систематическая составляющая погрешности измерений

1.13.1 Погрешность результата измерений(погрешность измерения) - отклонение результата измерения от истин­ного (действительного) значения измеряемой величины.

Истинное значение физической величи­ны неизвестно и его применяют лишь в теоретических исследованиях и расчетах. На практике используют действительное значение ФВ х_д ~ х_и , в результате чего погрешность измерения Δх_изм определяют по формуле

Δх_изм= х_изм - х_д ,

где х_изм - измеренное значение величины (х_д ~ х_и).

В качестве истинного значения при многократных изме­рениях параметра выступает

среднее арифметическое зна­чение х

х_и = х_ср = 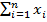. (2)

1.13.2 Систематическая погрешность– это составная часть всей погрешности результата измерения, не изменяющаяся или изменяющаяся закономерно при многократных измерениях одной и той же величины. Обычно систематическую погрешность пытаются исключить возможными способами (например, применением методов измерения, снижающих вероятность ее возникновения), если же систематическую погрешность невозможно исключить, то ее просчитывают до начала измерений и в результат измерения вносятся соответствующие поправки.

В процессе нормирования систематической погрешности определяются границы ее допустимых значений.

Систематическая погрешность определяет правильность измерений средств измерения (метрологическое свойство).

Систематические погрешности в ряде случаев можно определить экспериментальным путем. Результат измерений тогда можно уточнить посредством введения поправки.

Поправка(С) - значение величины, которая одноименна с измеряемой, и вводится в

неисправленный результат измерения с целью устранения неисключенных составляющих

сис­тематической погрешности.

Знак поправки противоположен знаку погрешности: можно записать, что С = - Δ _с и тогда результат измерения х = х_д + Δ_с + С (численное значение С может быть как со знаком «+», так и со знаком «-»).

По­правку, прибавляемую к номинальному значению меры, называют поправкой к значению меры; поправку, вводимую в показание измерительного прибора, называют поправкой к показанию прибора.

Поправочный множитель - числовой коэф­фициент С_м, на который умножают неисправленный результат изме­рения для исключения влияния систематической погрешности измерений.

Поправочный множитель используют в случаях, когда систематическая погрешность пропорциональна значению измеряемой ФВ. Поправки и поправочные множители могут определять­ся теоретически или экспериментально, представляются в виде числа или функции, заданной графически, таблично или аналитическими выражениями.

1.13.3 Способы исключения систематических погрешностей делятся на четыре вида (а – б):

а) ликвидация причин и источников погрешностей до начала проведения измерений;

б) устранение погрешностей в процессе уже начатого измерения способами замещения, компенсации погрешностей по знаку, противопоставлениям, симметричных наблюдений;

в) корректировка результатов измерения посредством внесения поправки (устранение погрешности путем вычислений);

г) определение пределов систематической погрешности в случае, если ее нельзя устранить.

Ликвидация причин и источников погрешностей до начала проведения измерений.

Данный способ является самым оптимальным вариантом, так как его использование упрощает дальнейший ход измерений (нет необходимости исключать погрешности в процессе уже начатого измерения или вносить поправки в полученный результат).

Для устранения систематических погрешностей в процессе уже начатого измерения применяются различные способы:

- способ введения поправокбазируется на знании систематической погрешности и действующих закономерностей ее изменения. При использовании данного способа в результат измерения, полученный с систематическими погрешностями, вносят поправки, по величине равные этим погрешностям, но обратные по знаку;

- способ замещениясостоит в том, что измеряемая величина заменяется мерой, помещенной в те же самые условия, в которых находился объект измерения. Способ замещения применяется при измерении следующих электрических параметров: сопротивления, емкости и индуктивности;

- способ компенсации погрешности по знакусостоит в том, что измерения выполняются два раза таким образом, чтобы погрешность, неизвестная по величине, включалась в результаты измерений с противоположным знаком;

- способ противопоставленияпохож на способ компенсации по знаку. Данный способ состоит в том, что измерения выполняют два раза таким образом, чтобы источник погрешности при первом измерении противоположным образом действовал на результат второго измерения.

1.13.4 Определение неисключенной систематической погрешности. Если систематические погрешности невозможно исключить, то дают оценку доверительных границ неисключенной составляющей погрешности (НСП).

НСП результата измерения образуется из составляющих НСП метода, СИ или других источников. Например, приведенная погрешность СИ и неточность изготовления – неисключенные систематические погрешности.

В качестве границ составляющих НСП принимают, например, пределы основных и дополнительных погрешностей СИ, если случайные составляющие погрешности пренебрежимо малы.

При оценке границ НСП их рассматривают как случайные величины, распределенные по равномерному закону.

Границы неисключенной систематической погрешности θ при числе слагаемых т ≤ 3 вычисляют по формуле

θ = ± 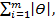(3)

где θ_i - граница i-й составляющей неисключенной систематической погрешности.

При числе неисключенных систематических погрешностей т ≥ 4 вы­числения проводят по формуле

θ = ± k 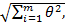(4)

где k — коэффициент зависимости отдельных неисключенных систематических погрешностей от выбранной доверительной вероятности Р_д при их рав­номерном распределении (при Р_д= 0,99 k =1,4; при Р_д= 0,95 k =1,1).

Здесь θ рассматривается как доверительная квазислучайная (т. е. почти случайная) погрешность.

1.14. Погрешность измерений. Случайная составляющая погрешности измерений

Случайная погрешность измерения Δ_сл 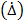- состав­ляющая погрешности результата измерения, изменяющаяся случай­ным образом (по знаку и значению) при повторных измерениях, про­веденных с одинаковой тщательностью,одной и той же физической величины.

В появлении таких погрешностей не имеется какой-либо закономерности, они проявляются при повторных измерениях в виде некоторого разброса полученных результатов.

Наличие случайных погрешностей и их значение определяют степень точности измерений.

Практически случайные погрешности неизбежны, неустранимы и всегда имеют место в результате измерений.

Их описание и оценка возможны только на основе теории вероятности, методов математи­ческой статистики и положений теории информации.

Случайные по­грешности нельзя исключить из результатов измерений введением поправки.

Однако их можно уменьшить путем многократного изме­рения физической величины и последующей статистической обработ­кой полученных результатов.

Если не учитывать промахи, абсолютная погрешность измерения представляется суммой систематической и случайной составляющих

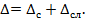
Это означает, что абсолютная погрешность, как и результат из­мерений, является случайнойвеличиной.

1.15. Характер распределения случайной погрешности

1.15.1 Случайная погрешность 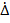или ∆_сл – это составляющая погрешности измерения, которая изменяется в тех же условиях измерения случайным образом.

Случайная погрешность обнаруживает себя при многократных измерениях и при условии исключения систематических погрешностей.

Характер распределения случайных погрешностей – рассеяние результатов измерения относительно центра рассеяния, которым является условно истинное - действительное или среднее значения.

Рассеяние результатов в ряду измерений - несовпа­дение результатов измерений одной и той же величины в ряду равно­точных измерений, как правило, обусловленное действием случайных погрешностей.

Причины возникновения случайных погрешностей не поддаются изучению. Известно, что случайная погрешность образуется под действием множества причин, действующих одновременно и вызывающих рассеяние результатов в ряду измерений. Случайные погрешности могут иметь как положительное, так и отрицательное значения.

Случайную погрешность исключить из результата измерений нельзя, ее можно только лишь уменьшить при обработке результата многократных измерений методами математической статистики (теории вероятности).

1.15.2 Количественную оценку рассеяния результатов в ряду измерений вследствие воздействия случайных погрешностей обычно получают после введения поправок на действие систематических погрешно­стей измерений.

Оценками рассеяния результатов в ряду измерений ФВ могут быть:

- размах;

- средняя арифметическая погрешность (по модулю);

- средняя квадратическая погрешность или стандартное отклонение;

- доверительные границы погрешности (доверительная граница или дове­рительная погрешность).

Закон распределения случайных погрешностей – это всякое соотношение, устанавливающее связь между возможными значениями случайной погрешности и соответствующими им вероятностями. Приэтом про случайную погрешность при измерениях говорят, что онаподчинена определенному закону распределения погрешностей.

Для количественной оценки распределения вероятности исполь­зуют вероятность события

х - х_д< Δ,

где х_д — действительное значе­ние измеряемой величины;

Δ — текущая погрешность с заданной вероятностью.

Вероятность этого события зависит от погрешности Δ и является некоторой функ­цией Δ.

Функцию F(Δ) называют функцией распределения вероятно­сти(интегральной функцией распределения, интегральным закономраспределения)случайной величины х

F(Δ) = Р(х – х_д<Δ).

Интегральный закон распределения отражает вероятность Р того, что случайная погрешность Δ находится в интервале от - ∞ до значения, меньшего граничного Δ_г

,

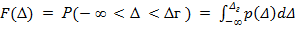где p(Δ) — плотность вероятности.

Функция распределения вероятности является универсальной ха­рактеристикой и существует для всех случайных величин (погрешно­стей) — и дискретных, и непрерывных.

Некоторые свойства инте­гральной функции распределения формулируют таким образом: функ­ция F(Δ) определена так, что F (- ∞) = 0 и F (∞) = 1.

Дифференциальным законом распределения случайной пог­решности Δ или плотностью распределения вероятностей(коротко — плотностью вероятности) случайной

погреш­ности Δ называют функцию

p(Δ) = .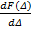

Числовые характеристики случайных погрешностей. Описание случайных погрешностей с помощью законов распределения р(Δ)или F(Δ)является наиболее полным.

Однако экспериментальное определение плотностей вероятности сопряжено с

определенными сложностями.

Вместе с тем во многих случаях не обязательно описы­вать погрешность полностью, а достаточно охарактеризовать число­выми параметрами лишь отдельные ее свойства. Такие параметры в математике называют числовыми характеристиками случайной вели­чины (погрешности)или моментами.

Часто погрешности вычисляют по числовым характе­ристикам: среднему значению х_ср (математическому ожиданию m₁ – начальный момент первого порядка)

для непрерывных случайных величин m₁= ,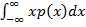

для дискретных случайных величин х_ср = ,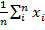

и дисперсии D – центральному моменту второго порядка

для непрерывных случайных величин D = ,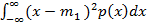

для дискретных случайных величин D = .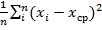

Для характеристики рассеяния случайной погрешности в единицах измерения

используется среднее квадратичное отклонение (СКО) σ

для непрерывных случайных величин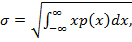

для дискретных случайных величин .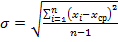

1.15.3 Доверительная вероятность соот­ветствует вероятности пребывания истинного (действительного) значения измеряемойфизической величиныв некотором случайном (доверительном) интервале значений от х - Δ_г до х + Δ_г

Р_д = Р ( - Δ_г ≤ Δ ≥ + Δ_г).

При определении доверительных границ (доверительных интерваловпогрешностей) задают доверительную вероятность (если она не задана условиями измерительной задачи). Для некоторого за­данного или полученного закона распределения погрешностей вероятность Р_д однозначно зависит от границ погрешности и возрастает с их увеличени­ем.

Чем большепринятое значение Р_д, темболее надежно будет рассчитан интервал, но тем шире будут границы,т. е. надежность значений границ будет выше.

Для плотностей вероятности, описываемыми симметричными относительно начала координат зависимостями, нижнюю и верхнюю границы погрешности измерений выбирают также симметричными относительно начала координат (рисунок 6).

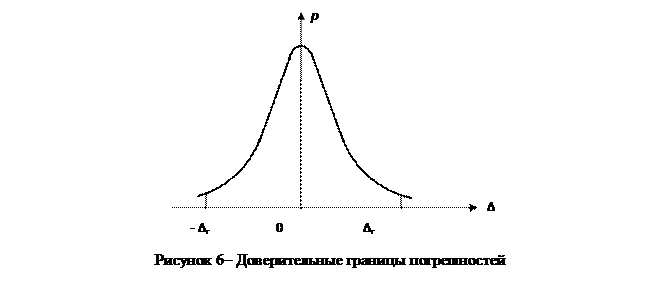
Доверительные границы в случае нормального за­кона распределения

(± tσ;± tσ_ср),

где σ, σ_ср - средние квадратические отклонения соответственно единичного и среднего арифметическо­го результатов п числа единичных измерений;

t - коэффициент, зависящий от доверительной вероятности Р_ди числа измерений n.

Среднее квадратическое отклонение среднего арифметическо­го результатов п числа единичных измерений вычисляют для дискретных случайных величин по формуле

.

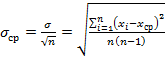Итак, для характеристики случайной погрешности надо обязательно задать минимум два числа — значение самой погрешности (или доверительные границы для нее) и доверительную вероятность.

1.15.4 Представление результатов измерений. Основной задачей любых измерений является извлечение с за­данной точностью и достоверностью количественной информации о ФВ. Поскольку измерения практически всегда сопровождаются появлением случайных погрешностей, то представление результатов измерений должна включать в себя действительное значение и довери­тельные границы, в которых находится ее истинное значение с заданной доверительной вероятностью (если не указано особо, то в метрологии подразумевается доверительная вероятность ).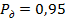

При многократных измерениях окончательный результат записывают в виде 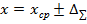при вероятности .

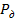При однократных измерениях результат измерения записывают в виде

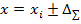при вероятности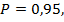

где 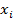– результат, зафиксированный СИ;

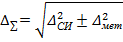— суммарная погрешность измерения, определяемая классом точности

СИ (Δ_си) и методической погрешностью (Δ_мет), если случайная погрешность

,

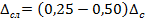где 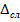– случайная составляющая погрешности измерения;

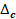– систематическая составляющая погрешности измерения.

Доверительные границы погрешности результата измерений (доверительный интер­вал) - наибольшее и наименьшее значения погреш­ности измерений, ограничивающие интервал, внутри которого с за­данной вероятностью находится искомое (истинное) значение по­грешности результата измерений (рисунок 5).

1.16. Виды распределения случайных погрешностей.

1.16.1 Наиболее часто применяемые законы распределения случайных погрешностей: нормальный (гауссов) при числе измерений n ≥ 30, Стьюдента при нормальном распределения погрешностей и числе измерений n < 30, равномерный закон и треугольный закон (закон Симпсона ).

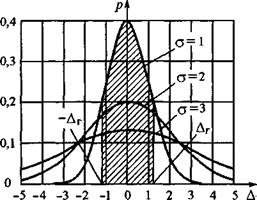1.16.2 Нормальный закон (закон Гаусса). Плотность распределения случайной погрешности р(Δ).

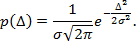
Интеграл вероятностей случайной погрешности (функция Лапласа)

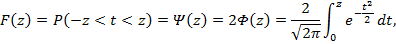
где z = Δ_г/σ.

Функция Ф(z), называемая функцией Лапласа, выражает вероят­ность попадания случайной величины t в интервал (0, z). Значения функции Ф(z) приведены в таблицах интеграла вероятностей.

Задаваясь границей Δ_г в долях σ, находят, а затем иско­мую вероятность 2Ф(z) по таблицам функции Ф(z). При необходимости можно выполнить обратный поиск, т. е. по заданной вероятности 2Ф(z) найти z, далее Δ_г = z∙σ и интервал (- Δ_г, Δ_г). Функция Ф(z) – нечетная функция: Ф(-z) = - Ф(z).

Практическое значение интервалов погреш­ностей (-Δ_г, Δ_г), представленных в долях СКО σ. В частности:

- Р(-2σ/3 < Δ < 2σ/3) = 0,5;

- P(- σ < Δ < σ) = 0,683;

- Р(- σ < 2Δ < σ) = 0,95;

- Р(-3σ < Δ < Зσ) = 0,997;

- Р(- ∞ < Δ < +∞) = 1.

Если распределение вероятности случайной погрешности подчи­няется нормальному закону (а это довольно часто встречается на практике), то вместо значения Δ указывается σ. В соответствии со значениями этих вероятностей погрешность результатов измерений, равная (2/3)σ, названа равновероятной (поскольку Р = 0,5). Погреш­ность, равная Зσ, принята за максимальную. При вероятности Р= 0,997 из тысячи выпол­ненных измерений только три их погрешности Δ выходят за пределы интервала (-Зσ, Зσ).

Значения интеграла вероятностей представлены таблицей 6.

Таблица 6 - Значение интеграла вероятностей F(z) =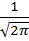

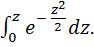
z	Ф(z)	z	Ф(z)	z	Ф(z)	z	Ф(z)
0,00	0,0000	0,70	0,2580	1,40	0,4192	2,25	0,4878
0,02	0,0080	0,72	0,2642	1,42	0,4222	2,30	0,4893
0,04	0,0160	0,74	0,2703	1,44	0,4251	2,35	0,4906
0,06	0,0239	0,76	0,2764	1,46	0,4279	2,40	0,4918
0,08	0,0319	0,78	0,2823	1,48	0,4306	2,45	0,4929
0,10	0,0398	0,80	0,2881	1,50	0,4332	2,50	0,4938
0,12	0,0478	0,82	0,2939	1,52	0,4357	2,55	0,4946
0,14	0,0557	0,84	0,2995	1,54	0,4382	2,60	0,4953
0,16	0,0636	0,86	0,3051	1,56	0,4406	2,65	0,4960
0,18	0,0714	0,88	0,3106	1,58	0,4429	2,70	0,4965
0,20	0,0793	0,90	0,3159	1,60	0,4452	2,75	0,4970
0,22	0,0871	0,92	0,3212	1,62	0,4474	2,80	0,4974
0,24	0,0948	0,94	0,3264	1,64	0,4492	2,85	0,4978
0,26	0,1026	0,96	0,3315	1,66	0,4515	2,90	0,4981
0,28	0,1103	0,98	0,3365	1,68	0,4535	2,95	0,4984
0,30	0,1179	1,00	0,3413	1,70	0,4554	3,00	0,49865
0,32	0,1255	1,02	0,3461	1,72	0,4573	3,10	0,49903
0,34	0,1331	1,04	0,3508	1,74	0,4591	3,20	0,49931
0,36	0,1406	1,06	0,3554	1,76	0,4608	3,30	0,49952
0,38	0,1480	1,08	0,3599	1,78	0,4625	3,40	0,49966
0,40	0,1554	1,10	0,3643	1,80	0,4641	3,50	0,49977
0,42	0,1628	1,12	0,3686	1,82	0,4656	3,60	0,49984
0,44	0,1700	1,14	0,3729	1,84	0,4671	3,70	0,49989
0,46	0,1772	1,16	0,3770	1,86	0,4686	3,80	0,499928
0,48	0,1844	1,18	0,3810	1,88	0,4699	3,90	0,499952
0,50	0,1915	1,20	0,3849	1,90	0,4713	4,00	0,499968
0,52	0,1985	1,22	0,3888	1,92	0,4726	5,00	0,499999
0,54	0,2054	1,24	0,3925	1,94	0,4738
0,56	0,2123	1,26	0,3962	1,96	0,4750
0,58	0,2190	1,28	0,3997	1,98	0,4761
0,60	0,2257	1,30	0,4032	2,00	0,4772
0,62	0,2324	1,32	0,4066	2,05	0,4798
0,64	0,2389	1,34	0,4099	2,10	0,4821
0,66	0,2454	1,36	0,4131	2,18	0,4842
0,68	0,2517	1,38	0,4162	2,20	0,4861