Сравнимые понятия делятся на совместимые и несовместимые.

Совместимые понятия имеют полное или частичное совпадение объемов. У них нет признаков, которые это запрещают. Совместимость включает:

- равнозначность, где мыслится один и тот же предмет. Объемы понятий при этом полностью совпадают;

- пересечение, где имеется частичное совпадение объемов и наличие ряда общих признаков;

- отношения подчинения, где объем меньшего, подчиненного понятия входит в состав большего по объему.

Несовместимые понятия имеют отношения:

- соподчинение (координация), где в общее родовое понятие входят два или более видовых понятий;

- противоположность (контрарность), где одно из понятий отрицает признаки другого понятия;

- противоречие (контрадикторность), где одно из понятий содержит некоторые признаки, а другие их отрицают.

1) Равнозначность 1) Соподчинение

2) Перекрещивание 2) Противоположность

3) Подчинение 3) Противоречие

ЛОГИЧЕСКИЕ ОПЕРАЦИИ С ПОНЯТИЯМИ.

Определением называется логическая операция, которая позволяет отличить изучаемый предмет от других предметов и установить значение того или иного слова или термина. В определении главным является раскрытие содержания предмета с помощью уже известных понятий.

В зависимости от того, что определяется, сам предмет или его обозначение, определения бывают реальными и номинальными.

Реальные это определения предметов, то есть того, что представляет собой предмет.

Номинальные – обозначают то или иное слово, или выражение. Номинальные определения используют слова «называется», «называют».

Определения бывают явные, в которых определяющее и определяемое понятия равны. Наиболее распространенным методом явного определения, известным со времен Аристотеля, является определение через ближайший род и видовое отличие.

Сущность определения состоит в указании на ближайший род, видом которого выступает определяемое нами понятие. При работе с понятиями следует иметь в виду правила явного определения и возможные ошибки.

1. Определение должно быть соразмерным, то есть определяющее и определяемое понятия должны быть равны. При этом следует избегать ошибки чрезмерно широкого определения, когда объем определяющего понятия шире объема определяемого. Определение не должно содержать круга, тавтологии или фиксации того же, через то же.

2. Определение должно быть четким, ясным и недвусмысленным. Оно должно определятся через известное, не содержать метафор и отрицания.

В науке и практической деятельности широко применяются неявные определения. К их видам относятся:

- семантическое определение, где определенному обозначению соответствует предмет, через описание его признаков;

- синтаксическое определение описывает предмет через правила оперирования с ним;

- контекстуальное определение выясняет содержание незнакомого слова по смыслу целостного текста или речи;

- в остенсивных определениях значения слов выясняют путем показа предметов.

С определением понятий тесно связана операция деления понятий. Если с помощью определения раскрывается содержание понятия, то с делением более полно характеризуется его объем.

Поскольку объем понятия представляет целый класс предметов, то в ходе деления выясняется из каких подклассов состоит исходное понятие.

Деление конкретизирует знание о предметах, соответствующих делимому понятию.

Главное условие: деление должно производится по единому признаку или основанию деления. Объем понятия, который подлежит делению, называется объемом делимого понятия, а результат членами деления. Отношение класса и подкласса, рода и вида понятия фиксирует таксономическое деление. Таксономия это расположение по порядку. Это систематизирует отношение понятии, распределяет их на виды по каким-либо основаниям.

Таксономическое деление идет: по видовому признаку, дихотомическим путем и классифицированием.

Деление по видовому признаку требует четкого распределения родового понятия на виды при соблюдении соразмерности деления, где объем делимого понятия должен быть равным сумме объемов членов деления. Например; понятие туризм делится на внутренний и международный. Ошибкой является отсутствие некоторых членов деления или лишние мнения в этом процессе. Деление производится по одному основанию. При двух и более основаниях происходит перекрещивание объемов членов деления.

Члены деления должны полностью исчерпать объем делимого понятия, быть непрерывными. То есть члены деления должны быть соподчиненными понятиями. В рамках дихотомического деления происходит выделение двух противоречащих видовых понятий. Оно всегда соразмерно, так члены деления исключают друг друга.

Классификация является распределением предметов по классам согласно сходству и различию между ними. В отличие от деления, классификация идет только по существенным признакам и служит для систематизации знаний. Классификации бывают научными, искусственными и вспомогательными.

Операции обобщения и ограничения понятия позволяют существенно уточнить его объем. Логическая операция обобщения понятий это переход от видового понятия к родовому, с большим объемом, но меньшим содержанием.

Ограничение понятия – операция обратная обобщению, где переход от родового понятия к видовому сопровождается дополнением первого родом видообразующих признаков. Операции ограничения и обобщения основаны на законе обратного соотношения между объемом и содержанием понятия.

4. СУЖДЕНИЯ, ИХ ВИДЫ И ОТНОШЕНИЯ МЕЖДУ НИМИ.

1. Сущность, структура и виды суждении.

2. Распределенность терминов в простых категорических суждениях.

3. Отношения между основными видами атрибутивных суждений. Логический квадрат.

4. Логические связи в сложных суждениях.

Мысль доступна другим людям при её выражении в языковой форме. Формой выражения высказываний являются предложения. Но не всякое предложение – высказывание /суждение/. Вопрос или просьба не несут в себе утверждения или отрицания чего-либо.

Поэтому языковой формой суждения является повествовательное предложение, в котором утверждается или отрицается связь между предметом и его признаком, отношения между предметами или формой их существования.

Суждения атрибутивны, если в них утверждается или отрицается связь между предметом или его признаком, отношения предметов или формы их существования. Поэтому суждения либо истинны, либо ложны. Суждения раскрывают смысл понятий через их связь друг с другом, в качестве элементов целого. Если в понятии выражается предметный характер мышления, то в суждении реализуется активное отношение человека к окружающей среде. В нем фиксируются, в первую очередь, связи и отношения между предметами и их свойствами.

Выражая отношения между индивидами, суждение реализует коммуникативную функцию с целью сообщения и получения новой информации. Для этого, по мысли И. Канта, необходимо в познавательном и коммуникативном процессах использовать и проявлять силу суждения.

Логика выделяет в структуре суждения субъект, предикат, связку и квантор. Субъект это логическое подлежащее или понятие о предмете суждения. Субъект обозначается буквой S. Предикат суждения это понятие о признаках предмета, о котором идет речь в суждении. Обозначается буквой Р. Связка это отношение между предметом мысли и его свойствами, выражается союзами (есть, суть, неверно: либо, либо) и простым согласованием слов.

Квантор, это слово, которое указывает, относится ли суждение ко всему объему понятия, выражающего субъект, или к его части. Выражается словами: «все», «ни один», «некоторые» и т.д.

В каждом суждении имеется качественная и количественная характеристика. Термин «качество» употребляется в логике исключительно для характеристики наличия или отсутствия свойств у предмета.

По качеству суждения бывают утвердительные или отрицательные. В утвердительных суждениях говорится о наличии свойства у предмета или принадлежности предмета субъекту, то есть S есть Р.

Например, все туристы путешественники.

Отрицательные суждения говорят об отсутствии свойств у предмета, т.е. S не – есть Р, или S есть не – Р.

Количество суждений означает полный класс предметов или только его часть, о чем идет речь в данном суждении.

Существует объединенная классификация простых суждений:

- Общеутвердительные суждения – общие по количеству и утвердительные по качеству, формулировка суждения: Все S суть Р. Обозначаются буквой А.

- Общеотрицательные – общие по количеству и отрицательные по качеству. Формулировка суждения: ни одно S не есть Р. Обозначается буквой Е.

- Частноутвердительные – ограниченные по количеству и утвердительные по качеству. Формула: некоторые S есть Р. Обозначаются буквой J.

- Частноотрицательные суждения – ограниченные по количеству и отрицательные по качеству. Формула: некоторые S не есть Р. например: некоторые студенты не знают логику. Обозначаются буквой О.

Для выражения отношений субъекта и предиката используется операция распределения терминов в суждении.

Термин считается распределенным, если его объем полностью включен или полностью исключен из объема другого термина. Термин нераспределен, если его объем частично включается в объем другого термина или исключается из него.

Распределенность терминов в суждениях отражена в таблице:

	S	P
A	+	- (+)
E	+	+
J	-	- (+)
O	-	+

Соблюдается правило: субъект распределен в общем предикате в отрицательном суждение.

Отношения между сравнимыми суждениями хорошо прослеживаются на основе логической схемы (логического квадрата):

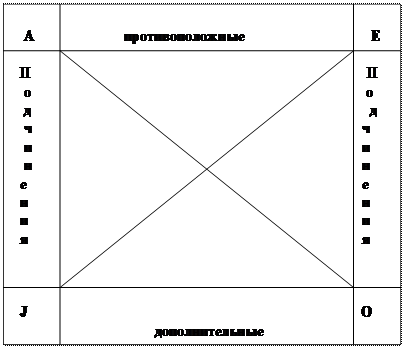Операции превращения и обращения связаны с анализом внутренней структуры суждения и связи между высказываниями.

Непосредственными умозаключениями являются превращенные и обращенные категорические суждения.

Превращения категорического суждения это изменение его качества одновременно с заменой предиката на противоречащий ему термин. Это

А все S суть Р________ J некоторые S суть Р

Ни одно S не суть не Р некоторые S не суть не Р

Е ни одно S не суть Р О некоторые S не суть Р

Все S суть не Р некоторые S суть не Р

Обращение категорического суждения заключается в перемене местами субъекта и предиката.

А все S суть Р обращается с ограничением

Некоторые Р суть S

J некоторые S суть Р Е ни один S не суть Р

Некоторые Р суть S ни один Р не суть S

О. Частноотрицательные суждения не обращаются

5. УМОЗАКЛЮЧЕНИЕ: СУЩНОСТЬ И СТРУКТУРА

Все знания о мире делятся на непосредственные (эмпирические) и опосредованные (выводные). В первом случае это результат непосредственного изучения окружающего мира. Но большая часть знаний получается опосредованно, путем построения логических выводов.

Итак, умозаключение – это форма мышления, посредством которой из одного или нескольких определений, истинность которых доказана, с необходимостью выводится суждением, содержащее новое знание. Структура умозаключения содержит посылки и вывод или заключение.

Посылки – это суждения, из которых делается вывод. Они содержат известное знание и должны быть истинными. Вывод (заключение) – новое суждение, полученное из посылок в ходе умозаключающей деятельности.

ВИДЫ УМОЗАКЛЮЧЕНИЙ:

По количеству посылок	По характеру посылок и связок	По направлению мысли
Непосредственные Дедуктивные Индуктивные Традуктивные (по аналогии)	Категорические Разделительные Условные Разделительно-категорические Условно-категорические Условно-разделительные	Дедуктивные Индуктивные Традуктивные

При получении истинного вывода необходимо строго руководствоваться нормативными требованиями мышления с учетом характера фигур, правил терминов и посылок умозаключения.

Наиболее часто встречающимся типом умозаключений являются дедуктивные умозаключения. Дедукция – это переход от знания большей степени общности к знанию меньшей степени общности.

Наиболее известным типом дедуктивного умозаключения является простой категорический силлогизм, в котором из двух категорических суждений (посылок), связанных общим термином, получается новое суждение – вывод.

Все люди (М) смертны (Р).

Сократ (S) – человек (М)

Сократ (S) – смертен (Р)

Посылки связаны общим термином –(М – медиум, посредник). М – входит в посылки, но отсутствует в заключении. В выводе предикат шире субъекта по объему. Поэтому предикат вывода – больший термин, а субъект вывода – меньший термин. Соответственно, посылки в которые входят больший и меньший термины, называются большей посылкой и меньшей посылкой. В зависимости от положения среднего термина зависит качественный и количественный характер вывода. Существуют четыре положения среднего термина, что соответствует четырем фигурам категорического силлогизма:

I M P II. P M

M

M

III. M P IV. P М

M S M S

Существуют особые правила фигур:

I фигура: большая посылка – общая, меньшая утвердительная.

II фигура: большая посылка – общая, одна из посылок – отрицательная

III фигура: меньшая посылка – утвердительная, заключение частное.

IV фигура: общеутвердительного заключения не дает.

Общие правила категорического силлогизма:

Правила терминов:

1. Из двух отрицательных посылок нельзя сделать вывода.

2. Из двух частных посылок нельзя сделать вывода.

3. Если одна из посылок отрицательная, то и заключение отрицательное.

4. Если одна из посылок частная, то заключение частное.

Модус, или вид, это качественные и количественные разновидности посылок и вывода из них. Всего из 256 модусов – 19 правильных. Модус характеризует соблюдение правил и истинности вывода.

Правильные модусы:

1 фигура: ААА, ЕАЕ, АJJ, EJO.

2 фигура: AEE, AOO, EAE, EJO.

3 фигура: AAJ, EAO, JAJ, OAO, EJO.

4 фигура: AAJ, AEE, JAJ, EAO, EJO.

Энтимема (в уме) – сокращенный категорически силлогизм, в котором пропущена посылка или заключение, когда не требуется высказывать известные истины.

. Более глубокое представление о содержании дедуктивной логики дают по характеру посылок и выводов дают условные, условно – категорические и разделительные силлогизмы. В условном умозаключении обе посылки и вывод – условные суждения. Его структура:

Если а, то в

Если в, то с__

Если а, то с

Условно – категорическое умозаключение содержит одной из посылок условное суждение, другой – простое категорическое суждение. Достоверное заключение, с необходимостью следующее из посылок дает утверждающий и отрицающий модусы. Его схема:

Если а, то в

___а___

В

Отрицающий модус позволяет строить достоверные умозаключения от отрицания следствия и отрицанию основания. Например:

Если а, то в

___не - в___

Не - а

В разделительно-категорическом силлогизме одна из посылок должна быть разделительным суждением. В умозаключении по утверждающе – отрицающему модусу производится отрицание последством утверждения.

а или в, или с

____а____

Не-в и не-с

В разделительном силлогизме по отрицающие – утверждающему модусу утвержение производится путем отрицания. Например

А или в, или с

__не-а и не-в__

С

Кроме того, весьма важное значение имеют условно – разделительные умозаключения, где одна посылка условная, другая разделительная. Это умозаключение называют лемматическим (предположительно слепым). Оно может быть дилеммой, трилеммой и т.д., в зависимости от числа условных посылок.

ИНДУКТИВНЫЕ УМОЗАКЛЮЧЕНИЯ И УМОЗАКЛЮЧЕНИЯ ПО АНАЛОГИИ.

Индуктивные умозаключения являются разновидностью выводного знания при его движении от фактов к обощениям. Индуктивные умозаключения образуются в ходе практической деятельности, при сравнении однородных явлений и поиске их общей причины. Индукция – это умозаключение от знания меньшей степени общности к знанию большей степени общности. Схема индуктивного мышления.

Предметы А,В,С,D имеют признак Р

Предметы А, В, С, D принадлежат классу S

Следовательно все S есть Р

Основанием индуктивного мышления служат объективные, закономерные связи и отношения, где предметы должны быть однотипными (одного класса). В индуктивном умозаключении даже из достоверных посылок, вывод, как правило, вероятностный.

Различается полная, неполная и математическая индукция. В рамках полной индукции вывод о свойствах класса предметов делается на основании изучения его отдельных частей. Неполная индукция дает знание о классе предметов на основании изучения части предметов данного класса.

Если в популярной индукции объекты выбираются случайно, то в научной изучаются планомерно, наиболее типичные, на основе контрольных партий и замеров. Это позволяет сделать научное заключение о необходимых причинно-следственных связях и законах.

Повышению степени вероятности и истинности индуктивных умозаключений служит ряд методов. Это методы научной индукции (иначе методы Бэкона – Милля). С их помощью индуктивная логика устанавливает причинно-следственные связи при различных условиях протекания явлений.

- Метод сходства основан на поиски общего фактора исследуемого явления, при различных условиях его обнаружения. Исключая из этих условий исходные признаки можно выявить общий фактор, который и будет причиной данного явления.

Формула метода и сходства гласит, что если:

При условии А, В, С возникло явление Q

При условии А, К, L возникло явлении Q

При условии А, Р, Q возникло явлении Q

Вероятно А есть причина Q

Метод различия указывает, что если наличие или отсутствие признака вызывает или устраняет явлении, то этот признак причина явления. Так если:

При условии А, В, С, D происходит явлении d

При условии А, В, С отсутствует явление d

Вероятно D есть причина d

Метод сопутствующих изменений говорит о соответствии одних изменений и величин других. Изменение предшествующего обстоятельства есть либо его следствие, либо находится с ним в причинном отношении.

При условии А, В,С,D существует явление Q

При условии A1,B,C,D существует явление Q1

Следовательно, обстоятельство А есть причина Q

6. АРГУМЕНТАЦИЯ И ДОКАЗАТЕЛЬСТВО

Умение и потребность обоснованно доказывать положения и суждения в ходе полемики, беседы и других форм общения важный показатель правильного мышления и профессиональной компетентности. При этом студенту важно понять, что содержание логического знания необходимо для овладения искусства аргументации и рационального убеждения.

Доказательство – это логический прием обоснования истинности суждения с помощью других истинных суждений. Содерожание доказательства включает в себя тезис, основание (аргументы) и форму доказательства или демонстрацию. Тезис – это суждение или положение, истинность которого требуется доказать.

По способам доказательство делится на прямое, косвенное и генетическое. Прямое доказательство использует неоспоримые факты, а также обоснование аргументами истинности тезиса. Это ответы на экзаменах, научные споры, доказательство в суде и другое. В тоже время юридические доказательства, с опорой на факты, являются частными суждениями и из них нельзя получить дедуктивного умозаключения. В косвенном доказательстве вначале доказывают антитезис и, убедившись в его ложности, доказывают истинность тезиса. Антитезисом могут выступать одно или несколько суждений. В зависимости от этой структуры антитезиса косвенные доказательства делятся на : апагогические ( от противного) и разделительные.

В первом случае путем опровержения антитезиса доказывается истинность тезиса. Этот путь часто используется в математике, когда в теореме о непересекаемости двух перпендикуляров к одной прямой допускается их пересечение. Антитезис показывает возможность опущения из одной точки на прямую двух перпендикуляров, что противоречит аксиоме об одном перпендикуляре на прямую из одной точки. Антитезис ложен, следовательно, истинен тезис.

Разделительное доказательство основано на установлении истинности тезиса путем последовательного исключения всех элементов разделительного суждения или гипотез, кроме одного, достаточного аргумента.

Генетическое доказательство применяется при установлении происхождения и развития термина концепции в научных и исторических исследованиях. Для практики особенно важно убедиться в их истинности на основе подлинных источников. При этом для студента важно понять, что нормой доказательства являются:

- умение применять все виды доказательства

- использовать только истинные тезис и аргументы

- опираться на подлинные факты, имеющие отношение к тезису

- не применять неясных, двусмысленных и противоречивых тезисов и аргументов

- способы доказательства должны соответствовать законам логики, чтобы не появились возможные ошибки

К логическим ошибкам, вследствие неправильного использования правил доказательства и опровержения относятся паралогизмы, софизмы и парадоксы.

Паралогизм, или неправильное рассуждение, появляется вследствие неправильного вывода, незнания предмета или законов логики.

Софизм – это преднамеренная ошибка, сознательное нарушение правил логики, рассчитанное на ввод противника в заблуждение, стремление выдать ложь за истину. Это «кривая речь» или «мнимая мудрость» Если паралогизмы возникают случайно, то софизмы это нарушение правил и сознательное отвлечение внимания от главного утверждения.

Парадокс – это необычное явление или высказывание, которое резко расходится с действительностью. Они возникают из-за неясности, противоречий исходных принципов и норм познания. Таков классический парадокс «Что я говорю – ложно». Решение парадокса требует выхода за уровень данной системы рассмотрения объекта. В то же время парадоксы приводят к глубинным открытиям. Это создание теории иррациональных чисел, парадоксы теории множеств и многое другое.

В ходе общения важно не только умение отстаивать свои положения, но и опровергать позицию собеседника. Этому служит логический прием опровержения или разрушения доказательства путем установления ложности ранее выдвинутого тезиса.

Структура опровержения включает:

- Тезис опровержения; суждение, которое необходимо опровергнуть

- Аргументы опровержения, суждения, при помощи которых опровергается тезис

- Демонстрацию – логическую форму построения опровержения

При доказательстве антитезиса ( опровержения от противного) установление его ложности по закону исключенного третьего указывает на истинность тезиса.

При раскрытии приема критики аргументов следует обратить внимание на их прямое (косвенное) опровержение с помощью опыта и фактов или же через закон достаточного основания. То есть аргументы, требующие доказательства, не являются достаточными основаниями.

На ложность аргументов указывает их сомнительный источник.

Критика демонстрации говорит об ошибках в доказательстве, отсутствии логической связи между доказываемым тезисом и аргументами. При опровержении следует внимательно следить за соблюдением правил умозаключения. Истинности опровержения служит соблюдение ряда нормативных правил:

- Противоположные положения не опровергаются без тщательного рассмотрения

- Необходимо учитывать возможные ошибки наших аргументов

- Следует сочетать прямые и косвенные методы опровержения

Кроме того, следует строго соблюдать правила по отношению к тезисам, аргументам и демонстрации.

ВОПРОСЫ К ЗАЧЕТУ ПО КУРСУ ЛОГИКА

1. Предмет и задачи логики как науки.

2. Диалектическая логика и логика формальная: проблема соотношения.

3. Закон непротиворечия как базовый закон формальной логики.

4. Закон тождества.

5. Закон исключенного третьего.

6. Закон достаточного основания.

7. Основные этапы в развитии логики.

8. Общие представления о понятии как о форме мышления.

9. Виды понятий и основные операции с ними.

10. Ограничение и обобщение понятий.

11. Определение понятий.

12. Сущность классификации и ее принципы.

13. Суждение как форма мышления.

14. Простое суждение и его структура.

15. Правила соотношений суждений по истиннности. Логический квадрат.

16. Виды сложных суждений.

17. Суждение и вопрос.

18. Умозаключение, его роль в познании.

19. Дедукция.

20. Простой категорический силлогизм.

21. Некатегорические силлогизмы.

22. Полная и неполная индукция.

23. Научная индукция, методы Бэкона – Милля.

24. Аналогия.

25. Прямое и косвенное доказательство.

26. Опровержение.

27. Софизмы.

28. Виды аргументации.

29. Правила аргументации.

30. Спор как разновидность аргументации.

ВОПРОСЫ К ЭКЗАМЕНУ ПО КУРСУ ЛОГИКА

1. Предмет и задачи логики как науки.

2. Диалектическая логика и логика формальная: проблема соотношения.

3. Закон непротиворечия как базовый закон формальной логики.

4. Закон тождества.

5. Закон исключенного третьего как отражение альтернативности мира.

6. Закон достаточного основания.

7. Основные этапы развития логики.

8. Понятие как форма мышления.

9. Виды понятий и основные операции с ними.

10. Отношения между понятиями.

11. Обобщение и ограничение понятий.

12. Определение понятий.

13. Сущность классификации и ее принципы.

14. Суждение как форма мышления.

15. Простое суждение и его структура.

16. Распределенность терминов в суждении и его основные правила.

17. Правила соотношения суждений по истинности. Логический квадрат.

18. Виды сложных суждений.

19. Суждение и вопрос.

20. Умозаключение и его роль в познании.

21. Непосредственные умозаключения и их разновидности.

22. Простой категорический силлогизм и его аксиома.

23. Фигуры и модусы категорического силлогизма.

24. Некатегорические силлогизмы.

25. Индуктивные умозаключения.

26. Методы Бэкона-Милля.

27. Аналогия.

28. Гипотеза.

29. Доказательство.

30. Опровержение.

31. Софизмы и логические парадоксы.

32. Сущность аргументации и ее структура.

33. Правила аргументации и ошибки в ней.

34. Спор: правила и этика спора.

35. Общие представления о принятии решений.

36. Принятие решений в условиях неопределенности, определенности и риска.

37. Логика разрешения конфликтов

38. Риторика как составная часть практической логики.

39. Формы речи и функциональные стили.

40. Правила и законы риторики.

41. Стратегия и тактика публичных выступлений.

42. Проблемные ситуации.

ЛИТЕРАТУРА

1. Астафьев В.К. Законы мышления в формальной и диалектической логике. Львов, 1979.

2. Белнап И., Стил Г. Логика вопросов и ответов. М., 1981.

3. Бочаров В.А., Маркин В.И. Основы логики.- М.,1999.

4. Виноградова З.И. Логика научного управления. - М.,1998.

5. Войшвилло Е.К. Понятие как форма мышления. М., 1989.

6. Гетманова А.Д. Логика. - М.,1995.

7. Гетманова А.Д. Логика: словарь и задачи. - М.,1998.

8. Гетманова А.Д. Учебник по логике. М., 1994.

9. Горский Д.П. Определение. М., 1975.

10. Градовой Д.И. Логика в предпринимательской деятельности и деловом общении. - М.,1998.

11. Григорьев Б.В. Классическая логика. - М.,1996.

12. Зарецкая Е.Н. Логика речи для менеджера. М.,1997.

13. Ивин А.А. Логика. - М.,1999.

14. Ивин А.А. Логика. М., 1999.

15. Ивин А.А.,Никифоров А.Л. Словарь по логике. - ,М.,1998.

16. Ивлев Ю.В. Логика. - М.,1997.

17. Кириллов В.И. Упражнения по логике. - М.,1999.

18. Кириллов В.И., Старченко А.А. Логика. М., 1995.

19. Кондаков Н.И. Логический словарь. М., 1971.

20. Курбатов В.И. Логика. Ростов-на-Дону,1997.

21. Малахов В.П. Основы формальной логики. Учебное пособие для экономистов. М., 1999.

22. Новиков О.А., Уваров С.А. Коммерческая логика. - СПб.,1995.

23. Новиков О.А.,Уваров С.А. Коммерческая логика., СПб.,1995.

24. Рузавин Г.И. Логика и аргументация. - М.,1997.

25. Светлов В.А. Практическая логика. - СПб.,1997.

26. Светлов В.А. Практическая логика. СПб., 1997.

27. Свинцов В.И. Логика. М.,1998.Берков В.Ф. Логика: задачи и упражнения, практикум. - Минск,1998.