Обработка результатов наблюдений и оценивание

погрешностей измерений[4]

Оценку погрешности результата измерения выполняют при разработке МВИ. Источниками погрешностей являются модель ОИ, метод измерения, СИ, оператор, вляющие факторы условий измерений, алгоритм обработки результатов наблюдений. Как правило, погрешность результата измерения оценивается при доверительной вероятнйсти Р = 0,95.

При выборе значения Р необходимо учитывать степень важности (ответственности) результата измерений. Например, если ошибка в измерении может привести к гибели людей или к тяжелым экологическим последствиям, значение Р должно быть увеличено.

1. Измерения с однократными наблюдениями. За результат измерения в этом случае принимают результат однократного наблюдения х(с введением поправки, если она имеется), используя предварительно полученные (например, при разработке МВИ) данные об источниках, составляющих погрешность.

Доверительные границы НСП результата измерения Q(P)вычисляют по формуле

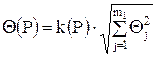, (3.3)

где k(P) - коэффициент, определяемый принятой Р и числом m₁ составляющих НСП: Q(P)- найденные нестатистическими методами границы

j-ой составляющей НСП (границы интервала, внутри которого находится эта составляющая, определяемые при отсутствии сведений о вероятности ее нахождения в этом интервале). При Р = 0,90 и 0,95 k(P) равен 0,95 и 1,1, соответственно при любом числе слагаемых m_1. При Р = 0,99 значения k(P) следующие (табл. 3.3):

Таблица 3.3

m1	k(P)	m1	k(P)
5 и более	1,45		1,30
	1,40		1,20

Если составляющие НСП распределены равномерно и заданы доверительными границами Q(P),то доверительную границу НСП результата измерения вычисляют по формуле

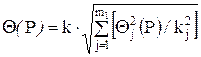, (3.4)

где k и k_j - те же, что и в предыдущем случае, коэффициенты, соответствующие доверительной вероятности РиР_j соответственно; m₁ - число составляющих НСП.

Среднее квадратическое отклонение (СКО) результата измерения с однократным наблюдением вычисляют одним из следующих способов:

1. Если в технической документации на СИ или в МВИ указаны нормально распределенные составляющие случайной погрешности результата наблюдения (инструментальная, методическая, из-за влияющих факторов, оператора и т.д.), то СКО вычисляют по формуле

,

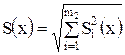где m₂ - число составляющих случайной погрешности; S_i - значения СКО этих составляющих.

Доверительную границу случайной погрешности результата измеренияя Î(Р) в этом случае вычисляют по формуле

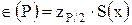, (3.5)

где z_P/2 - значение нормированной функции Лапласа в точке Р/2при доверительной вероятности Р(табл. 3.4):

Таблица 3.4

Р	zP/2	Р	zP/2
0,90	1,65	0,97	2,17
0,95	1,96	0,98	2,33
0,96	2,06	0,99	2,58

2. Если в тех же документах случайные составляющие погрешности результата наблюдения представлены доверительными границами Î_i(P) при одной и той же доверительной вероятности P, то доверительную границу случайной погрешности результата измерения с однократным наблюдением при доверительной вероятности вычисляют по формуле

.

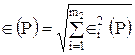3. Если случайные составляющие погрешности результата наблюдения определяют предварительно в реальных рабочих условиях экспериментальными методами при числе наблюденийи n_i <30, то:

,

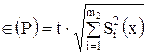где t - коэффициент Стьюдента, соответствующий наименьшему числу наблюдений n_min из всех n_i, можно найти в [4] или в любом справочнике по теории вероятностей; S(x) - оценки СКО случайных составляющих погрешности результата наблюдения, определяемых по формуле (3.10). Если в эксперименте невозможно или нецелесообразно определить СКО составляющих случайной погрешности и определено сразу суммарное СКО, то в формуле (3.5) m₂ = 1.

4. Если случайные составляющие погрешности результата наблюдений представлены доверительными границами Î(P_i), соответствующими разным вероятностям Р_i, то сначала определяют СКО результата измерения с однократным наблюдением по формуле

,

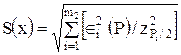где z_Pi/2 - значения функции Лапласа. Затем вычисляют Î(P) по формуле (3.4).

Для суммирования систематической и случайной составляющих погрешностей рекомендуется следующий способ:

Если Q(P)/S(x) < 0,8, (3.6)

то НСП Q(P) пренебрегают и окончательно принимают Î(P) за погрешность результата измерения D(P) при доверительной вероятности Р.

Если Q(P)/S(x) > 0,8, (3.7)

то пренебрегают случайной погрешностью и принимают D(P) = Q(P).

Если 0,8 £ Q(P)/S(x) £ 8, то доверительную границу погрешности результата измерений вычисляют по формуле

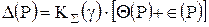, (3.8)

где K_S(g) = ; .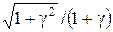

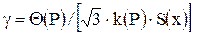2. Измерения с многократными наблюдениями. Обработку результатов в этом случае рекомендуется начать с проверки на отсутствие промахов (грубых погрешностей). Промах — это результат x_п отдельного наблюдения, входящего в ряд из nнаблюдений, который для данных условий измерений резко отличается от остальных результатов этого ряда. Если оператор в ходе измерения обнаруживает такой результат и достоверно находит его причину, он вправе его отбросить и провести (при необходимости) дополнительное наблюдение взамен отброшенного.

При обработке уже имеющихся результатов наблюдений произвольно отбрасывать отдельные результаты нельзя, так как это может привести к фиктивному повышению точности результата измерения. Поэтому применяют следующую процедуру. Вычисляют среднее арифметическое 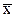результатов наблюдений х_i по формуле

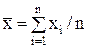. (3.9)

Затем вычисляют оценку СКО результата наблюдения как

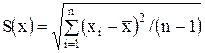. (3.10)

Находят отклонение v_п предполагаемого промаха x_пот :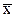

v_п = |x_п- | .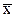

По числу всех наблюдений n (включая x_п) и принятому для измерения значению Р (обычно 0,95) по [4] или любому справочнику по теории вероятностей находят z(P,n) — нормированное выборочное отклонение нормального распределения. Если v_п < z×S(x), то наблюдение x_п не является промахом; если v_п ³ z×S(x), то x_п — промах, подлежащий исключению. После исключения x_пповторяют процедуру определения 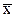и S(x) для оставшегося ряда результатов наблюдений и проверки на промах наибольшего из оставшегося ряда отклонений от нового значениям (вычисленного исходя из n - 1).

За результат измерения принимают среднее арифметическое 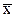[см. формулу (3.9)] результатов наблюдений х_i. Погрешность 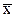содержит случайную и систематическую составляющие. Случайную составляющую, характеризуемую СКО результата измерения, оценивают по формуле

.

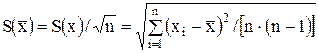В предположении принадлежности результатов наблюдений х_i к нормальному распределению находят доверительные границы случайной погрешности результата измерения при доверительной вероятности Р по формуле Î(P) = t(P,n) × S( 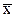) , (3.11)

где t - коэффициент Стьюдента.

Доверительные границы Q(Р) НСП результата измерения с многократными наблюдениями определяют точно так же, как и при измерении с однократным наблюдением — по формулам (3.3) или (3.4).

Суммирование систематической и случайной составляющих погрешности результата измерения при вычислении D(Р) рекомендуется осуществлять с использованием критериев и формул (3.6 – 3.8), в которых при этом S(x) заменяется на S( 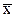) = S(x)/ .

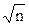3. Косвенные измерения. Значение измеряемой величины А находят по результатам измерений аргументов а₁, . . . , а_i,…a_m, связанных с искомой величиной уравнением

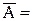f(a₁,….a_i….a_m). (3.12)

Вид функции f определяется при установлении модели ОИ.

Косвенное измерение при линейной зависимости. Искомая величина А связана с m измеряемыми аргументами уравнением

,

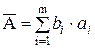где b_i - постоянные коэффициенты.

Предполагается, что корреляция между погрешностями измерений a_i отсутствует. Результат измерения Авычисляют по формуле

,

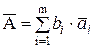где 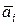— результат измерения a_i с введенными поправками. Оценку СКО результата измерения S(A) вычисляют но формуле

,

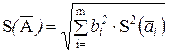где 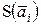— оценка СКО результата измерений .

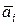Доверительные границы Î(Р) случайной погрешности 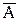при нормальном распределении погрешностей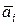

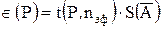, (3.13)

где t(P,n_эф) — коэффициент Стьюдента, соответствующий доверительной вероятности Р (обычно 0,95, в исключи­тельных случаях 0,99) и эффективному числу наблюдений n_эф , вычисляемому по формуле

,

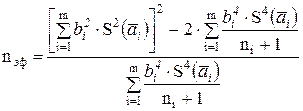где n_i —число наблюдений при измерении а_i.

Доверительные границы Q(Р) НСП результата такого измерения, сумму Q(Р) и Î(Р) для получения окончательного значения D(Р) рекомендуется вычислять с использованием критериев и формул (3.3), (3.4), (3.6) — (3.8), в которых m₁, Q_i, и S(x) заменяются, соответственно, на m, b_i×Q_i, и S( ).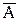

Косвенные измерения при нелинейной зависимости. При некоррелированных погрешностях измерений а_i используется метод линеаризации путем разложения функции f(а₁, . . . , a_m) в ряд Тейлора, то есть

f(а₁, . . . , a_m) = ,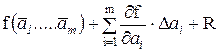

где 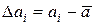— отклонение отдельного результата наблюдения а_i от 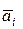; R — остаточный член.

Метод линеаризации допустим, если приращение функции f можно заменить ее полным дифференциалом. Остаточным членом

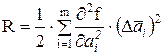пренебрегают, если ,

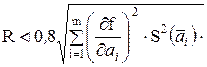где 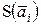— оценка СКО случайных погрешностей результата измерения 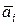. При этом отклонения D 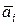должны быть взяты из возможных значений погрешностей и такими, чтобы они максимизировали R.

Результат измерения 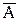вычисляют по формуле 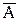= f( .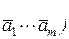

Оценку СКО случайной составляющей погрешности результата такого косвенного измерения S( 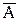) вычисляют по формуле

,

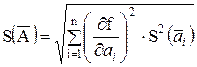а Î(Р) — по формуле (3.13). Значение n_эф , границы НСП Q(Р) и погрешность D(Р) результата косвенного измерения при нелинейной зависимости вычисляют так же, как и при линейной зависимости, но с заменой коэффициентов b_i на ¶f/¶a_i

Метод приведения (для косвенных измерений с нелинейной зависимостью) применяется при неизвестных распределениях погрешностей измерений a_i и при корреляции между погрешностями a_i для получения результата косвенного измерения и определения его погрешности. При этом предполагается наличие ряда n результатов наблюдений a_ij измеряемых аргументов а_i. Сочетания a_ij, полученных в j-м эксперименте подставляют в формулу (3.12) и вычисляют ряд значений A_j измеряемой величины А. Результат измерения 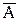вычисляют по формуле .

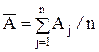Оценку СКО S( 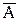) - случайной составляющей погрешности 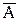-вычисляют по формуле

,

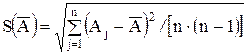а Î(Р) —по формуле (3.11). Границы НСП Q(Р) и погрешность D(Р) результата измерения 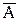определяют описанными выше способами для нелинейной зависимости.