Признак равносильности формул 4 страница
(1) 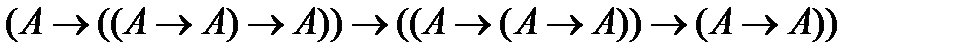 (в аксиоме (А2) мы подставили вместо формул А, В, С соответственно формулы
(в аксиоме (А2) мы подставили вместо формул А, В, С соответственно формулы 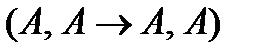 ;
;
(2) 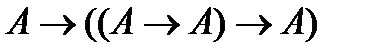 (в аксиоме (А1) вместо формулы В подставлена формула
(в аксиоме (А1) вместо формулы В подставлена формула 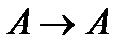 );
);
(3) 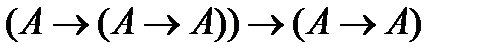 (из (1) и (2) по правилу МР)
(из (1) и (2) по правилу МР)
(4) 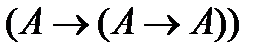 (в аксиоме (А1) вместо В подставлена формула А);
(в аксиоме (А1) вместо В подставлена формула А);
(5) 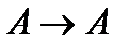 (из (3) и (4) по МР).
(из (3) и (4) по МР).
Пример 2.Покажем, что 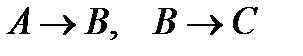 ├
├ 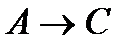 .
.
(1) 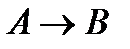 (гипотеза);
(гипотеза);
(2) 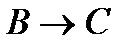 (гипотеза);
(гипотеза);
(3) 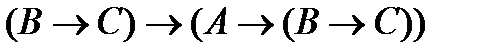 (подстановка в аксиому (А1) вместо формул А, В соответственно формул
(подстановка в аксиому (А1) вместо формул А, В соответственно формул 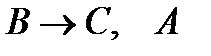 );
);
(4) 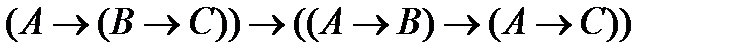 (Аксиома (А2));
(Аксиома (А2));
(5) 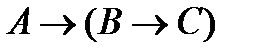 (из (1) и (3) по правилу МР);
(из (1) и (3) по правилу МР);
(6) 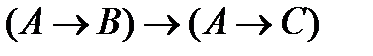 (из (4) и (5) по правилу МР);
(из (4) и (5) по правилу МР);
(7) 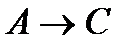 (из (1) и (6) по правилу МР).
(из (1) и (6) по правилу МР).
Процесс доказательства формул в аксиоматической теории высказываний значительно упрощается благодаря следующей теореме, которая называется теоремой о дедукции.
Теорема 1.Если F1, ..., Fn–1, Fn ├ G, то F1, ..., Fn–1 ├ Fn 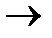 G. В частности, если F ├ G, то ├ F
G. В частности, если F ├ G, то ├ F 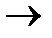 G.
G.
Рассмотрим несколько примеров, где используется теорема о дедукции.
Пример 3.Покажем, что 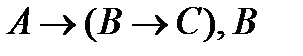 ├
├ 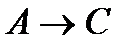 .
.
Покажем сначала, что 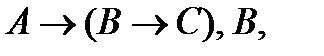 А├С.
А├С.
(1) В (гипотеза);
(2) А (гипотеза);
(3) 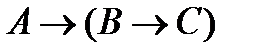 (гипотеза);
(гипотеза);
(4) 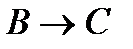 (из (2) и (3) по МР);
(из (2) и (3) по МР);
(5) С (из (1) и (4) по правилу МР).
Итак, 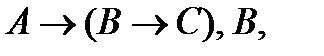 А├С, отсюда на основании теоремы о дедукции заключаем, что
А├С, отсюда на основании теоремы о дедукции заключаем, что 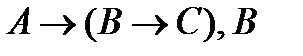 ├
├ 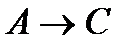 .
.
Пример 4. Покажем, что 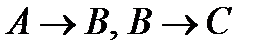 ├
├ 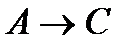 .
.
Установим сначала, что 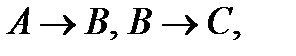 А├С.
А├С.
(1) 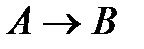 (гипотеза);
(гипотеза);
(2) 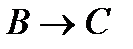 (гипотеза);
(гипотеза);
(3) А (гипотеза);
(4) В (из (1) и (3) по правилу МР);
(5) С (из (2) и (4) по правилу МР).
Поскольку 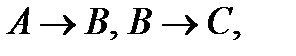 А├С, то на основании теоремы о дедукции мы заключаем, что
А├С, то на основании теоремы о дедукции мы заключаем, что 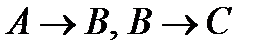 ├
├ 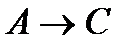 .
.
Пример 5. Покажем, что формула 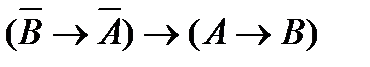 является теоремой. Покажем сначала, что
является теоремой. Покажем сначала, что 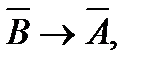 А ├ В.
А ├ В.
(1) 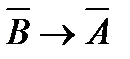 (гипотеза);
(гипотеза);
(2) А (гипотеза);
(3) 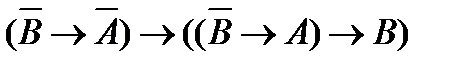 (аксиома (A3));
(аксиома (A3));
(4) 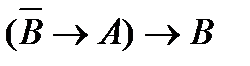 (из (1) и (3) по правилу МР);
(из (1) и (3) по правилу МР);
(5) 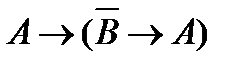 (аксиома(А1));
(аксиома(А1));
(6) 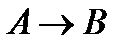 (из (4) и (5) согласно примеру 4);
(из (4) и (5) согласно примеру 4);
(7) 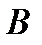 (из (2) и (6) согласно правилу МР).
(из (2) и (6) согласно правилу МР).
Итак, 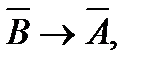 А ├ В. Применив теперь дважды теорему о дедукции, получаем требуемый результат.
А ├ В. Применив теперь дважды теорему о дедукции, получаем требуемый результат.
Отметим ряд важнейших свойств аксиоматической теории высказываний: полноту, разрешимость, непротиворечивость.
Теорема 2. (о полноте аксиоматической теории высказываний). Формула тогда и только тогда является теоремой аксиоматической теории высказываний, когда она является тавтологией алгебры высказываний.
Определение 5. Аксиоматическая теория называется непротиворечивой, если ни для какого утверждения А, сформулированного в терминах этой теории, само утверждение А и его отрицание 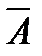 не могут быть теоремами данной теории. Если для некоторого утверждения А теории оба утверждения А и
не могут быть теоремами данной теории. Если для некоторого утверждения А теории оба утверждения А и 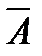 – теоремы этой теории, то аксиоматическая теория называется противоречивой.
– теоремы этой теории, то аксиоматическая теория называется противоречивой.
Заметим, что в противоречивой аксиоматической теории любая формула является теоремой.
Теорема 3. Аксиоматическая теория высказываний есть непротиворечивая аксиоматическая теория.
Определение 6.Аксиоматическая теория называется разрешимой, если существует алгоритм, позволяющий для любой формулы этой теории, ответить на вопрос, будет или нет эта формула теоремой этой теории.
Так как, используя таблицу истинности, мы можем для данной формулы эффективно определить, является ли она тавтологией или нет, то, как следствие теоремы 2, получаем следующие утверждение.
Теорема 4.Аксиоматическая теория высказываний есть разрешимая аксиоматическая теория.
Введем следующую важную характеристику аксиом аксиоматической теории.
Определение 7. Аксиома А данной аксиоматической теории называется независящей от остальных аксиом этой теории, если она не может быть выведена с помощью правил вывода из всех остальных аксиом. Система аксиом аксиоматической теории называется независимой, если каждая ее аксиома не зависит от остальных.
Теорема 5. Система аксиом (А1), (А2), (АЗ) аксиоматической теории высказываний независима.
Упражнение. Используя результаты настоящего раздела показать, что следующие формулы являются теоремами аксиоматической теории высказываний:
(1) 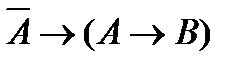 ; (3)
; (3) 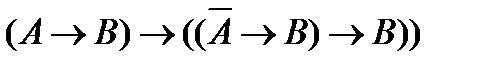 ;
;
(2) 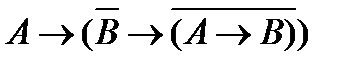 ; (4)
; (4) 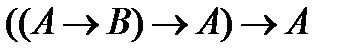 .
.
4. ПРАВИЛО РЕЗОЛЮЦИЙ
Автор данного правила – американский математик Робинсон, 1965 год.
Правило резолюций: 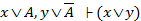 .
.
Введем новые понятия. Атом – это логическая переменная. Под дизъюнктом понимается элементарная дизъюнкция, то есть это дизъюнкция различных атомов или их отрицаний.
Это правило позволяет соединить две формулы, в одной из которых находится атом ( 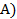 , а в другой отрицание атома (
, а в другой отрицание атома ( 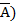 . Получается новая формула без этого атома.
. Получается новая формула без этого атома.
Доказательство. В логике высказываний имеет место тавтология:
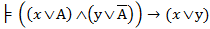
По теореме о равносильных утверждениях отсюда получаем
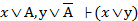 .
.
Частные случаи:1) 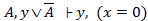
2) 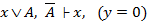
3) 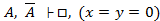 , где □ – пустой дизъюнкт (т.е. ложь).
, где □ – пустой дизъюнкт (т.е. ложь).
