Пределение доверительных интервалов случайной погрешности
Если гипотеза о нормальности закона распределения вероятности результата измерения доказана либо принята, стандартное отклонение среднего арифметического вычисляют по формуле
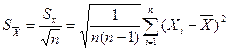(1.4.1)
Для расчётов обычно принимают доверительную вероятность
Р=0,95. Дополнительно проводят расчёт при Р=0,99 или, иными словами, 99%, при повышенных требованиях к точности.
При n > 40...50 порядок действий следующий.
Если результаты наблюдений Хi распределены нормально, то нормально распределены и величины Xi/n, а значит, и среднее арифметическое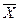 
, являющееся их суммой. Поэтому имеет место равенство:
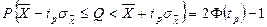
(1.4.2)
Таким образом, интервал, построенный с помощью среднего арифметического результатов n независимых повторных измерений ,в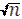 
раз короче интервала, вычисленного по результату одного измерения, хотя доверительная вероятность у них одинакова.
Потом определяют коэффициент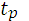 
при Ф( 
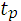)= (1+Р)/2 по таблице «Интегральная функция нормированного нормального распределения» (таблица 2 приложения) или по таблице «Значения функции Лапласа» при P/2.
Половина длины доверительного интервала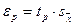 
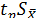называется доверительной границей погрешности результата измерений, а итог измерений записывается в виде:
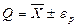; Р=…% (1.4.3)
При n<40…50 пользуются распределением Стьюдента.
Вероятность того, что дробь Стьюдента в результате выполненных наблюдений примет некоторое значение в интервале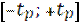 
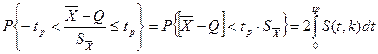(1.4.4)
Величины 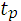, рассчитанные с помощью этой формулы для различных значений доверительной вероятности и числа степеней свободы k=n-1, табулированы (см.таблицу 5 приложения).
Рекомендуемая литература (теоретические вопросы):
1. Г.Д.Крылова «Основы стандартизации, сертификации и метрологии».
2. И.М.Лифиц «Стандартизация, метрология и сертификация».
3. Я.М.Радкевич, А.Г.Схиртладзе «Метрология, стандартизация и сертификация»
Нормативные документы
Рекомендации по обработке данных и расчету параметров описательной статистики.
Среднее арифметическое значение результата измерений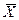 
,являются оценкой истинного значения Q :
,
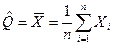Где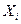 
- отдельные результаты измерений; n – число измерений.
Смещённая оценка дисперсии:
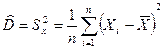
Несмещённая оценка дисперсии :
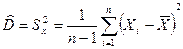
Среднее квадратическое отклонение или стандартное отклонение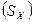 
,
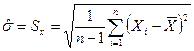
Среднее арифметическое отклонение:
.
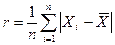Среднее квадратическое отклонение среднего арифметического :
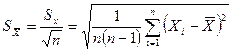
Примечание. После расчёта стандартного отклонения можно выявить грубые промахи по 3 сигма критерию (максимальное по абсолютной величине отклонение нормируют к стандартному отклонению, если эта величина превышает 3, то это значение считают грубым промахом, прибор бракуют, а результат исключают из обработки).
Допускается обработка данных с помощью электронных таблиц.
Задача: Обработка результатов многократных измерений при среднем числе опытов
Вариант назначается преподавателем.
Исходные данные: Результаты многократного измерения диаметра металлического стержня (мм).
Требуется : а) выявить результаты, содержащие грубую погрешность и избавиться от них;
б) оценить нормальность распределения результата наблюдения;
в) выполнить интервальную оценку.
Доверительную вероятность в пунктах а) и в) принимать равной Р= 0,95.
Пример решения.
а) Поскольку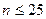 
, для выявления результатов , содержащие грубую погрешность, используем метод вычисления максимального относительного отклонения (критерий 
).
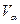Среднее арифметическое составляет:
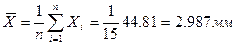
| Внимание! При расчёте 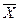необходимо на промежуточных этапах при округлении сохранять на один разряд больше, чем было в исходных числах. |
Среднее квадратичное отклонение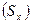 
определяется по формуле:
.
.
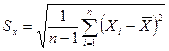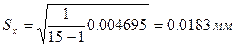Таблица № 1. Расчёт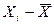 
и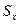 
(При n= 15).
| № |  | |  |
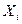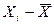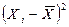| 2,99 | 0,003 | 0,000009 | |
| 2,98 | -0,007 | 0,000049 | |
| 2,98 | -0,007 | 0,000049 | |
| 2,99 | 0,003 | 0,000009 | |
| 2,98 | -0,007 | 0,000049 | |
| 2,98 | -0,007 | 0,000049 | |
| 2,98 | -0,007 | 0,000049 | |
| 3,05 | 0,063 | 0,003969 | |
| 2,98 | 0,003 | 0,000049 | |
| 2,99 | 0,003 | 0,000009 | |
| 2,99 | 0,003 | 0,000009 | |
| 2,99 | -0,007 | 0,000049 | |
| 2,98 | -0,007 | 0,000049 | |
| 2,97 | -0,017 | 0,000289 | |
| 2,98 | -0,007 | 0,000049 | |
| Сумма | 44,81 | 0,004695 | |
| Среднее | 2,987 |
Расчётные значения параметра для оценки возможного присутствия грубой погрешности вычисляются по формулам :
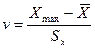или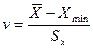 
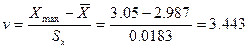
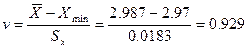
Критическое значение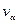 
определяется по таблице 6 приложения: при числе наблюдений n= 15 для уровня значимости 
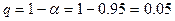находим 
.
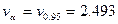Т.к. 3,443>2,493 (т.е.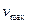 
> 
), 
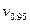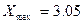содержит грубую погрешность; этот результат ( 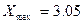м) отбрасывается.
Т.к. 0,929 <2,493 (т.е.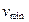 
< ), 
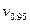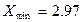мм не содержит грубую погрешность.
Проводим повторный расчёт по оставшимся значениям
Таблица №2. Расчёт 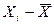и 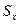(при n= 14).
| № | | | |
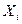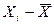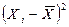| 2,99 | 0,007 | 0,000049 | |
| 2,98 | -0,003 | 0,000009 | |
| 2,98 | -0,003 | 0,000009 | |
| 2,99 | 0,007 | 0,000049 | |
| 2,98 | -0,003 | 0,000009 | |
| 2,98 | -0,003 | 0,000009 | |
| 2,98 | -0,003 | 0,000009 | |
| 2,98 | -0,003 | 0,000009 | |
| 2,99 | 0,007 | 0,000049 | |
| 2,99 | 0,007 | 0,000049 | |
| 2,99 | 0,007 | 0,000049 | |
| 2,98 | -0,003 | 0,000009 | |
| 2,97 | -0,013 | 0,000169 | |
| 2,98 | -0,003 | 0,000009 | |
| Сумма | 41,76 | 0,072 | 0,000486 |
| среднее | 2,983 | (сумма модулей) |
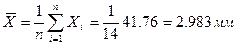
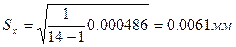
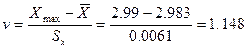
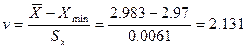
Критическое значение 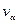определяется по таблице 6 приложения: при числе наблюдений n= 14 для 
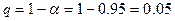находим 
.
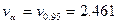Т.к. 1,148< 2.461 (т.е. < ),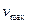 
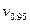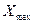= 2,99мм не содержит грубую погрешность;
Т.к. 2,131 < 2,461 (т.е. < ) ,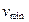 
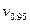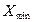= 2,97 мм так же не содержит грубую погрешность.
б)Т.к. 10…15< n<40…50, то для оценки нормальности применяем составной критерий.
Статистика dвычисляется по формуле
,
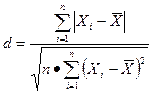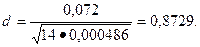
Задаемся уровнем значимости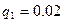 
.По таблице 7 приложения при числе измерений n= 14 
; 
.
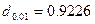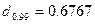Условие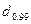 
< 
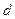
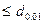; 0,6767<0.8729 
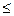0,9226 выполняется, поэтому в соответствии с первым критерием гипотеза о нормальности распределения принимается.
Для проверки по второму критерию в табл.8 приложения при n= 14 и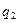 
= 0,02 находим 
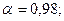m=1. В таблице 2 приложения находим значение 
.
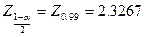Поскольку m= 1,то значение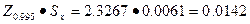 
мм может превзойти только одно из отклонений результатов наблюдений от среднего арифметического. В расчетной таблице №2 отклонений 
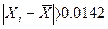мм нет ни одного. Таким образом, и второй критерий говорит о том , что экспериментальные данные при уровне значимости 
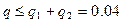не противоречат гипотезе о нормальности распределения результата наблюдения.
в)Т.к. гипотеза о нормальности закона распределения вероятности результата измерения подтверждена и n<40…50, проведем интервальную оценку с помощью коэффициентов Стьюдента.
Половина длины доверительного интервала:
.
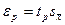Среднее квадратическое отклонение среднего арифметического:
.
.
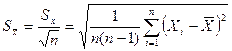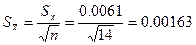По справочной таблице вида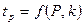 
“Распределение Стьюдента” ( табл. 5 приложения) при заданной доверительной вероятности P= 0,95 и числе степеней свободы k=n-1=14-1=13 определяем соответствующий коэффициент Стьюдента :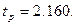 
Тогда
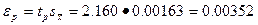мм
Ответ: 2,983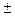 
0,004мм; Р= 95%.
| Внимание! При записи окончательного ответа погрешность округляется до того количества значащих цифр, которое требуется по правилам округления. Затем округляется 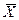до того же разряда, до которого была округлена погрешность. |