Чтобы перевести целое число из одной позиционной системы в другую, необходимо последовательно делить это число на ос­нование той системы, в которую оно переводится.

МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ЭОМ. СИСТЕМЫ СЧИСЛЕНИЯ.

ПЕРЕВОД ЧИСЕЛ ИЗ ОДНОЙ СИСТЕМЫ В ДРУГУЮ

Системой счисления называется совокупность приемов наиме­нования и записи чисел посредством цифр. Различают позицион­ные и непозиционные системы счисления.

В позиционной системе значение каждой цифры зависит от ее положения (позиции) в ряду цифр, изображающих число. Напри­мер, в числе 444 первая слева четверка означает количество сотен, содержащихся в числе, вторая — количество десятков, третья — количество единиц.

В непозиционной системе каждая цифра сохраняет свое зна­чение независимо от места ее положения в числе. Так, в числе XXX цифра X в любом месте означает число десять.

В цифровых вычислительных машинах используются пози­ционные системы счисления, так как непозиционные системы неудобны для вычислений.

Из позиционных систем наиболее распространенной является десятичная система счисления. Названа она так потому, что для записи чисел в ней используется десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9, изображающих целые числа от нуля до девяти. Число десять, являющееся основанием системы (основанием системы называется количество цифр, применяемых в системе), изобра­жается двумя цифрами в виде 10. Всякое другое число записы­вается в виде последовательности цифр, разделенных запятой на целую и дробную части.

Возьмем, например, число 3245,16 и раскроем его значение:

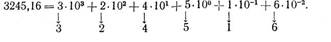Таким образом, в десятичной системе счисления любое число представляет собой сумму степенных членов, в которых основа­нием степени является число 10, а коэффициентами — цифры, образующие рассматриваемое число (они вынесены стрелками).

Если за основание системы принять различные числа (два, три, пять, восемь и т. д.), можно получить двоичную, троичную, пятиричную, восьмеричную и другие системы.

Особый интерес в машинной математике представляет двоич­ная система счисления. В этой системе для изображения чисел используются всего две цифры: 0 и 1. Основание системы счис­ления — число два — записывается как 10.

Чтобы перевести целое число из одной позиционной системы в другую, необходимо последовательно делить это число на ос­нование той системы, в которую оно переводится.

Полученные остатки, начиная с последнего, и будут «цифрами» при записи числа в новой системе счисления, т. е.

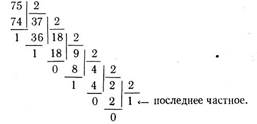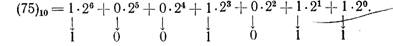Перевод десятичного числа 75 в двоичную систему счисления:

Таким образом,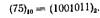

Как видно из последней записи, отличительной особенностью двоичной системы счисления является то, что она содержит мини­мально возможное количество цифровых знаков (0 и 1), а запись числа длинная Последнее обстоятельство делает ее практически непригодной для расчетов вручную.

Двоичная система счисления применяется в большинстве сов­ременных машин для представления чисел и выполнения опера ций. Арифметические операции проще всего выполняются в двоич­ной системе счисления (табл. 16).

Таблица 16

Арифметические операции в двоичной системе счисления

Выполнение арифметических операций над двоичными числами производится так же, как и над десятичными числами. Необхо­димо только учитывать, что сумма 1 + 1 дает нуль в данном раз­ряде и единицу переноса в следующий (старший) разряд.

Для примера найдем сумму двух чисел 111 (пятнадцать) и 100101 (тридцать семь). Напишем эти числа в столбец и сло­жим по общему правилу:

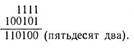
Для изображения чи­сел в цифровых машинах применяются элементы, способные находиться в од­ном из нескольких фикси­рованных состояний. Число таких состояний должно равняться числу цифр, которое имеет система счисления, применяемая в машине. В качестве таких элементов в электронной машине могут быть использованы реле, электронные лампы, конденсаторы и т. д. Они могут работать как двухпозиционные элементы по принципу действия: «Да—нет», «Включено—выключено». Если одно из них, например «Включено», будет соответствовать нулю, тогда другое («Выключено») — единице. Это удобно при Конст­руировании цифровых вычислительных машин. Кроме того, реали­зация арифметических и логических операций при помощи двоич­ных элементов с использованием двоичной системы проще. Пре­имущество двоичной системы заключается еще и в том, что она позволяет применить в цифровых вычислительных машинах аппа­рат математической логики.

В ЭВМ применяются две формы представления чисел: числа с фиксированной запятой и числа с «плавающей» запятой. Соот­ветственно и ЭВМ подразделяются на машины с фиксированной, и машины с «плавающей» запятой.

Для машин с фиксированной запятой при конструировании заранее устанавливают, какое количество разрядов выделяется для целой части числа, а какое для дробной. Обычно занятая фиксируется перед первым (старшим) цифровым разрядом, а ма­шина оперирует с цифрами меньше единицы. При решении задач на такой машине число масштабируют с таким расчетом, чтобы в процессе вычислений не получился результат, превышающий единицу или равный единице, так как в этом случае применяется разрядная сетка машины и искажается результат.