Минимизация логических функций, оптимизация технической реализации функций алгебры логики
Следующим шагом аналитического описания таблично заданной функции является минимизация полученного выражения. Очевидно, что запись, полученная в виде совершенной дизъюнктивной нормальной формы, в большинстве случаев может быть легко упрощена. Используем для этого свойства дистрибутивности и отрицаний:
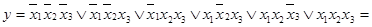
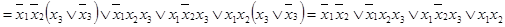 .
.
Полученная форма уже не является совершенной, так как не во всех минитермах присутствуют все переменные.
Дальнейшие преобразования подобного вида уже невозможны. Такая форма является тупиковой.
Здесь приведен только один из вариантов подобного преобразования. Вполне возможно, что какой-либо другой вариант даст более компактную запись. Дизъюнктивная нормальная форма, содержащая минимальное количество букв называется минимальной. Минимальная форма находится путем перебора всевозможных тупиковых форм.
Формулу для у можно преобразовать до более компактной, искусственно повторно добавив минитермы (подчеркнутые), уже присутствующие в записи. Подобная добавка не изменит значения функции, так как 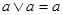 .
.
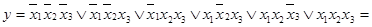
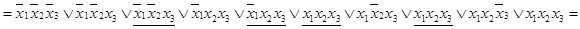
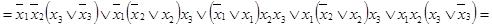
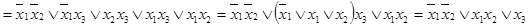
Очевидно, что полученная запись является существенно более компактной, чем исходная. Совершенная дизъюнктивная нормальная форма содержала 12 операций конъюнкции и 5 операций дизъюнкции. Полученная в итоге форма содержит всего 2 конъюнкции и 2 дизъюнкции. При аппаратной реализации это означает использование всего 4 элементов вместо 17 элементов в исходной схеме. На переключательной схеме из 18 ключей осталось только 5.
Каковы же преимущества подобной минимизации с точки зрения аппаратной реализации?
1. Повышение надежности системы. Если схемы строятся на одинаковой элементной базе, то схема с меньшим количеством элементов имеет более высокую надежность.
2. Повышение быстродействия. В любой схеме каждый из последовательно соединенных элементов вносит свое запаздывание, снижая общее быстродействие системы.
3. Удешевление системы. Система, имеющая меньшее число элементов является более дешевой как при изготовлении, так и при эксплуатации, обслуживании и ремонте. Кроме того, снижение общего количества элементов позволяет применять более дорогие и надежные комплектующие, что также снижает затраты на ремонт.
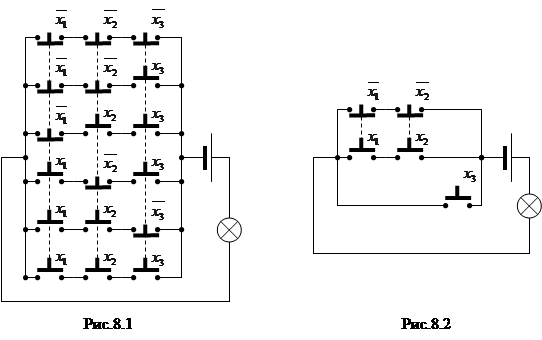
Переключательные схемы, реализующие совершенную дизъюнктивную нормальную форму и минимальную форму, представлены на рис.8.1 и рис.8.2.
 |
Вопросы и задания
8.1. Опишите аналитически (в виде совершенных конъюнктивной и дизъюнктивной нормальных форм) функции у1(х1,х2,х3), у2(х1,х2,х3), у3(х1,х2,х3), заданные таблично:
| х1 | х2 | х3 | у1 | у2 | у3 |
8.2. Найдите минимальную форму для каждой функции из предыдущего задания. Составьте переключательную схему для каждой из полученных минимальных форм.
