Основные позиции закона РФ «Об обеспечении единства измерений» от 26.06.2008 № 102 – ФЗ. 2 страница

Между числом и единицей измерения всегда оставляют один пробел, например сила тока I = 2 A.

Для безразмерных величин, у которых единицей измерения является «единица», единицу измерения принято опускать.

Численное значение ФВ зависит от выбора единицы. Одно и то же значение ФВ может иметь различные значения в зависимости от выбранных единиц, например, скорость автомобиля v = 50 м/с = 180 км/ч; длина волны одной из желтых натриевых полос λ = 5,896·10^{-7 м = 589,6 нм.}

Математические символы ФВ печатают курсивом (наклонным шрифтом), обычно это отдельные строчные или прописные буквы латинского или греческого алфавита, а с помощью нижнего индекса можно дополнить информацию о величине.

Обозначения единиц в тексте, набранным любым шрифтом, следует печатать прямым (ненаклонным) шрифтом. Они являются математическими единицами, а не аббревиатурой.

После них никогда не ставится точка (кроме случаев, когда они заканчивают предложение), они не имеют окончаний множественного числа.

Для отделения десятичной части от целой ставят точку (в документах на английском языке – относится в основном к США и Англии) или запятую (во многих европейских и языках других стран, в т.ч. Российской Федерации).

Для облегчения прочтения чисел с большим количеством цифр эти цифры могут быть объединены в группы по три как до, так и после запятой, например, 10 000 000.

При написании обозначений производных единиц обозначения единиц, входящих в производные, разделяют точками, стоящими на средней линии, например, Н·м (ньютон – метр), Н·с/м² (ньютон – секунда на квадратный метр).

Наиболее употребительно выражение в виде произведения обозначений единиц, возведенных в соответствующую степень, например, м²·с^-1.

При наименовании, соответствующем произведению единиц с кратными или дольными приставками, рекомендуется приставку присоединять к наименованию первой единицы, входящей в произведение. Например, 10³ Н·м следует именовать кН·м, а не Н·км.

1.4 Понятие о контроле и испытаниях

1.4.1 Некоторые понятия, связанные с определением«измерение».

Принцип измерений – физическое явление или эффект, положенные в основу измерения (механический, оптико-механический, эффект Доплера для измерения скорости движения объекта).

Методика выполнения измерений (МВИ) – установленная совокупность операций и правил при измерении, выполнение которых обеспечивает получение результатов с гарантированной точностью в соответствии с принятым методом.

Обычно МВИ регламентируется НТД, например, аттестацией МВИ. По существу МВИ – алгоритм измерения.

Наблюдения при измерении – операция, проводимая при измерении и имеющая целью своевременно и правильно произвести отсчет итога наблюдения – результат всегда случаен и представляет собой одно из значений измеряемой величины, подлежащей совместной обработке для получения результата измерения.

Не рекомендуется заменять термин «измерение» термином «наблюдение» (РМГ29 – 99).

Отсчет показаний - фиксация значения величины или числа по показывающему устройству СИ в заданный момент времени.

Например, зафиксированное в некоторый момент времени по шкалеизмерительной индикаторной головки значение, равное 4,52 мм,является отсчетом ее показания на этот момент.

Информативный параметр входного сигнала СИ – параметр входного сигнала, функционально связанный с измеряемой ФВ ииспользуемый для передачи ее значения или являющийся самойизмеряемой величиной.

Измерительная информация – информация о значениях ФВ. Зачастуюинформация об объекте измерения известна до проведения измерений, что является важнейшим фактором, обуславливающим эффективность измерения. Такую информацию обобъекте измерения называют априорной информацией.

Измерительная задача – задача, состоящая в определении значения ФВ путем ее измерения с требуемой точностьюв данных условиях измерения.

Объект измерения – тело (физическая система, процесс,явление), которые характеризуются одной или несколькими ФВ.

Например, деталь, длина и диаметр которой измеряются; технологический процесс, во время которого измеряют температуру.

Математическая модель объекта – совокупность математических символов и отношений между ними, которая адекватно описывает свойства объекта измерения.

При построении теоретических моделей неизбежно введение каких либо ограничений, допущений и гипотез.

Поэтому возникает задача оценки достоверности (адекватности) полученной модели реальному процессу или объекту. Для этого, когда это необходимо, проводят экспериментальную проверку разработанных теоретических моделей.

Алгоритм измерения – точное предписание о порядке операций, обеспечивающих измерение ФВ.

Область измерений– совокупность измерений ФВ, свойственных какой – либо области науки или техники и выделяющихся своей спецификой (механические, электрические, акустические и т. д.).

Неисправленный результат измерения – значение величины, полученное при измерении до введения в него поправок, учитываю систематические погрешности.

Исправленный результат измерения – полученное при измерении значение величины и уточненное путем введения в него необходимых поправок на действие систематических погрешностей.

Сходимость результатов измерений – близость друг к другу результатов измерений одной и той же величины, выполненных повторно одними и теми же СИ, одним и тем же методом в одинаковых условиях и с одинаковой тщательностью.

Наряду с термином «сходимость» в отечественных документах используют термин «повторяемость». Сходимость результатов измерений может быть выражена количественно через характеристики их рассеяния.

Воспроизводимость результатов измерений – близость результатов измерений одной и той же величины, полученных в разных местах, разными методами, разными средствами, разными операторами, в разное время, но проведенных к одним и тем же условиям измерений (температуре, давлению, влажности и др.).

Воспроизводимость результатов измерений может быть выражена количественно через характеристики их рассеяния.

Качество измерений – совокупность свойств, обуславливающих получение результатов измерений с требуемыми точностными характеристиками, в необходимом виде и в установленные сроки.

Достоверность измеренийопределяется степенью доверия к результату измерения и характеризуется вероятностью того, что истинное значение измеряемой величины находится в указанных пределах, или в указанном интервале значений величины.

Ряд результатов измерений – значения одной величины, последовательно полученные из следующих друг за другом измерений.

Среднее взвешенное значение величины -среднее значение величины из ряда неравноточных измерений, определенное с учетом веса каждого единичного измерения.

Среднее взвешенное значение еще называют средним весовым.

Вес результата измерений (вес измерений) – положительное число (р), служащее оценкой доверия к тому или иному отдельному результату измерения, входящему в ряд неравноточных измерений.

В большинстве случаев принято считать, что весá входящих в ряд неравноточных измерений обратно пропорциональны квадратам их средних квадратических погрешностей, т. е. p_i = 1/S_i ².

Для простоты вычислений обычно результату с большей погрешностью приписывают вес (р = 1), а остальные веса находят по отношению к данному «единичному» весу.

Измерение – нахождение значения ФВ опытным путем с помощью специальных технических средств.

Измерение включает в себя совокупность операций по применению технического средства, хранящего единицу ФВ, обеспечивающих нахождения соотношения измеряемой величины с ее единицей и получения значения этой величины.

Примеры: в простейшем случае, прикладывая линейку к какой - либо детали, по сути сравниваем ее размер с единицей, хранимой линейкой, и, произведя отсчет, получаем значение величины (длины, высоты); с помощью цифрового прибора сравнивают раз мер

ФВ, преобразованный в цифровое значение, с единицей, хранимой прибором, и проводят отсчет по цифровому табло прибора.

Понятие «измерение» отражает следующие его особенности (а – д):

а) приведенное определение понятия «измерение» удовлетворяет общему уравнению измерений, т.е. в нем учтена техническая сторона (совокупность операций), раскрыта метрологическая суть (сравнение измеряемой величины и ее единицей) и показан результат операций (получение значения величины);

б) измерять можно характеристики свойств реально существующих объектов материального мира;

в) процесс измерений – экспериментальный процесс (невозможно провести измерение теоретическим или расчетным путем);

г) для проведения измерения обязательным является использование технического СИ, хранящего единицу измерения;

д) в качестве результата измерения принимается значение ФВ (выражение ФВ в виде некоторого числа принятых для нее единиц).

От термина «измерение» происходит термин «измерять», которым широко пользуются на практике.

Не рекомендуется применять термины «мерить», «обмерять», «замерять», «промерять»

Не следует применять выражение «измерение значения», так как значение величины – это уже результат измерений.

Метрологическая суть измерения сводится к основному уравнению измерения (основному уравнению метрологии):

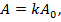
где А – значение измеряемой ФВ;

А_о – значение величины, принятой за образец;

k – отношение измеряемой величины к образцу.

Итак, любое измерение заключается в сравнении путем физического эксперимента измеряемой ФВ с некоторым ее значением, принятым за единицу сравнения, т.е. мерой.

Наиболее удобен вид основного уравнения метрологии, если выбранная за образец величина равна единице. В этом случае параметр k представляет собой числовое значение измеренной величины, зависящее от принятого метода измерения и единицы измерения.

Измерения включают в себя наблюдения.

Наблюдение при наблюдении – экспериментальная операция, выполняемая в процессе измерений, в результате которой получают одно значение из совокупности значений величины, подлежащих совместной обработке для получения результата измерений.

1.4.2 Следует различать термины «измерение», «контроль», «испытание» и «диагностирование».

Измерение- нахождение значения физической величины опытным путем с помощью специальных технических средств.

Измерение может быть как частью промежуточного преобразования в процессе контроля, так и окончательным этапом получения информации при испытании.

Технический контроль— это процесс определения соответствия установленным нормам или требованиям значения параметров изделия или процесса.

При контроле выявляется соответствие или несоответствие фактических данных требуемым и вырабатывается соответст­вующее логическое решение по поводу объекта контроля — «го­ден» или «негоден».

Контроль состоит из ряда элементарных действий:

- измери­тельного преобразования контролируемой величины;

- операции воспроизведения установок контроля;

- операции сравнения;

- опре­деления результата контроля.

Перечисленные операции во многом схожи с операциями измерения, однако процедуры измерения и контроля во многом различаются:

- результатом контроля является качественнаяхарактери­стика, а измерения - количественная;

- контроль осуществляется, как правило, в пределах относи­тельно небольшого числа возможных состояний, а измерение — в широком диапазоне значений измеряемой величины;

- основной характеристикой качества процедурыконтроля является достоверность, а процедуры измерения — точность.

Испытаниемназывается экспериментальное определение количественных и (или) качественных характеристик свойств объекта испытаний как результата воздействий на него при его функционировании, а также примоделировании объекта или (и) воздействия.

Экспериментальное определение при испытаниях указанных характеристик производится с помо­щью измерений, контроля, оценивания и формирования соответствующих воздействий.

Основными признаками испытаний являются:

- задание требуемых (реальных или моделируемых) условий испытаний (режимов функционирования объекта испытаний и (или) совокупности воздействующих факторов);

- принятие на основе результатов испытаний решений годности или негодности его, предъявления на другие испытания и т.д.

Показателями качества испытаний является неопределенность(погрешность),

повторяемость и воспроизводимостьрезультатов.

Диагностирование– процесс распознавания состояния элементов технического объекта в данный момент времени. По результатам диагностирования можно прогнозировать состояние элементов технического объекта для продолжения его эксплуатации.

1.4.3 Для проведения измерений с целью контроля, диагностирования или испытания необходимо проектирование измерений, в процессе которого выполняют следующие работы:

- анализ измерительной задачи с выяснением возможных источников погрешностей;

- выбор показателей точности измерений;

- выбор числа измерений, метода и средств измерений (СИ);

- формулирование исходных данных для расчета погрешностей;

- расчетотдельных составляющих и общей погрешности;

- расчет показателей точности и сопоставление их с выбранными показателями.

Все эти вопросы отражаютв методике выполнения измерений (МВИ).

1.5 Классификация измерений

1.5.1 Вид измерений – часть области измерений, имеющая свои особенности и отличающаяся однородностью измеряемых величин.

Измерения весьма разнообразны, что объясняется множеством измеряемых величин, различным характером их изменения во времени, различными требованиями к точности измерений и т.д.

В связи с этим измерения классифицируются по различным признакам (рисунок 1).

Равноточные измерения – ряд измерений какой-либо величины,выполненных несколькими одинаковыми по точности СИ в одних и техже условиях с одинаковой тщательностью.

Неравноточные измерения – ряд измерений какой-либо величины, выполненных различающими по точности СИ и (или) в разных условиях.

Однократное измерение – измерение, выполненное один раз. На практике во многих случаях выполняются однократные измерения, например, времени по часам, для производственных процессов.

Многократные измерения – измерение одного и того же размера ФВ, результат которого получен из нескольких следующих друг за другом измерений, т. е. состоящих из ряда однократных измерений.

Статические измерения – измерения ФВ, принимаемой в соответствии с конкретной измерительной задачей за неизменную напротяжении времени измерения.

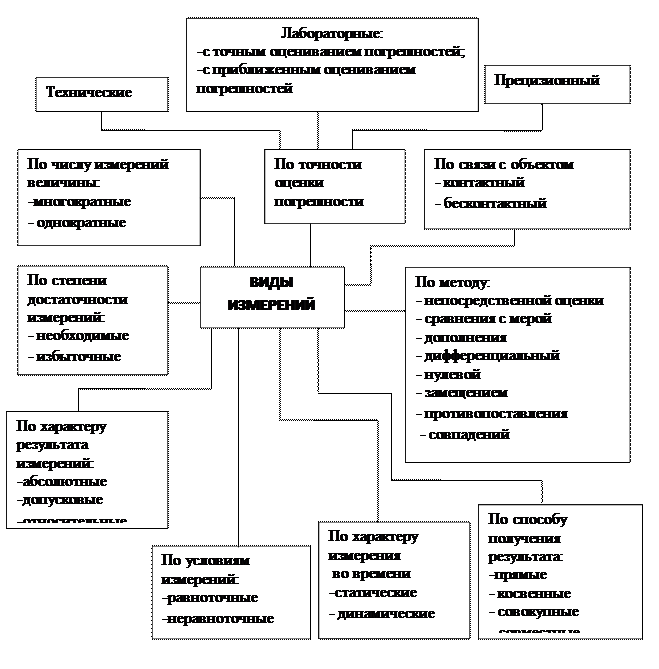
Рисунок 1 - Классификация видов измерения

Динамическое измерение – измерение изменяющейся по размеру ФВ. Результатом динамического измерения является функциональная зависимость измеряемой величины от времени, т. е. когда выходной сигнал изменяется во времени в соответствии с изменением измеряемой величины.

Абсолютные измерения – измерения, основанные на прямых измерениях одной или нескольких основных величин и (или) использовании значений физических констант.

Например, измерение длины пути при равномерном прямолинейном равномерном движении L = vt, основано на измерении основной величины – времени Т и использовании физической постоянной v.

Понятие абсолютное измерение применяется как противоположное понятию относительное измерение и рассматривается как измерение величины в ее единицах. В такой трактовке это понятие находит все большее применение.

Относительное измерение – измерение отношения величины к одноименной величине, играющей роль единицы, или измерение изменения величины по отношению к одноименной величине, принимаемой за исходную.

Относительные измерения при прочих равных условиях могут быть выполнены более точно, так как в суммарную погрешность результата измерений не входит погрешность меры ФВ.

Примеры относительных измерений: измерение отношений мощностей, давлений и т.д.

Метрологические измерения – измерения, выполненные с использованием эталонов.

Технические измерения – измерения, выполненные техническими СИ.

1.5.2 Прямое измерение – измерение ФВ, проводимое прямым методом, при котором искомое значение ФВ получают непосредственноиз опытных данных.

Прямое измерение производится путем сравнения ФВ с мерой этой величины непосредственно или путем отсчета показаний СИ по шкале или цифровому прибору, градуированных в требуемых единицах.

Часто под прямыми измерениями понимаются измерения, при которых не производятся промежуточных преобразований.

Примеры прямых измерений: измерение длины, высоты с помощью линейки, напряжения – с помощью вольтметра, массы с помощью пружинных весов.

Уравнение прямого измерения имеет следующий вид:

Q = q[Q].

Косвенное измерение – измерение, полученное на основе результатов прямых измерений других ФВ, функционально связанных с искомой величиной известной зависимостью.

Уравнение косвенных измерений имеет следующий вид:

Y = F(x₁, x₂…, x_i,… x_n),

Y = F(x),

где F – известная функция;

n – число прямого измерения ФВ;

x₁, x, x_i, x_n – значения прямого измерения ФВ.

Например, определение площади, объема с помощью измерения длины, ширины, высоты; электрической мощности методом измерения силы тока и напряжения и т. д.

Совокупные измерения – одновременно проводимые измерениянескольких одноименных величин, при которых искомое значение величины, определяют путем решения системы уравнений, получаемых при измерениях различных сочетаний этих величин.

Понятно, что для определения значений искомых величин число уравнений должно быть не меньше числа величин.

Пример: значение массы отдельных гирь набора определяют по известному значению массы одной из гирь и по результатам измерений (сравнений ) масс различных сочетаний гирь.

Имеются гири массами m₁, m_2, m₃.

Масса первой гири определится следующим образом:

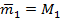
Масса второй гири определится как разность массы первой и второй гирь М_1,2 и измеренной массой первой гири m₁:

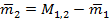
Масса третьей гири определится как разность массы первой, второй и третьей гирь М_1,2,3 и измеренных масс первой и второй гирь

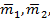
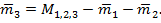
Часто именно этим путем добиваются повышения точности результатов измерения.

Совместные измерения – одновременно проводимые измерения нескольких неодноименных ФВ для определения зависимости между ними.

Пример1. Построение градуировочной характеристики Y = f(x) измерительного преобразователя, когда одновременно измеряют наборы значений:

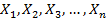
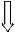
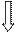
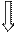
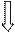
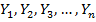
Значения ФВ определяется с помощью СИ конкретным методом.

1.6 Методы измерений

1.6.1 Метод измерений – прием или совокупность приемов сравнения измеряемой ФВ с ее единицей в соответствии с реализованным принципом измерений и использования СИ.

Конкретные методы измерений определяются видом измеряемых величин, их размерами, требуемой точностью результата, быстротой процесса измерения, условиями, при которых проводят измерения, и ряд других признаков.

В принципе каждую ФВ можно измерить несколькими методами, которые могут отличаться друг от друга особенностями как технического, так и методического характера.

Метод непосредственной оценки – метод измерений, при котором значение величины определяют непосредственно по отсчетному устройству СИ.

Быстрота процесса измерения делает его часто незаменимым для практического

использования, хотя точность измерения обычно ограничена. Примеры: измерение длины линейкой, массы – пружинными весами, давления – манометром.

Метод сравнения с мерой – метод измерений, в котором измеряемую величину сравнивают с величиной, воспроизводимой мерой (измерение зазора с помощью щупа, измерение массы на рычажных весах с помощью гирь, измерение длины с помощью концевых мер и т. д.).

В отличие от СИ непосредственной оценки, более удобной для получения оперативной информации, СИ сравнения обеспечивают бóльшую точность измерения.

Нулевой метод измерения – метод сравнения с мерой, в котором результирующий эффект воздействия измеряемой величины и меры на прибор сравнения доводят до нуля.

Например, измерение электрического сопротивления мостом с полным его уравновешиванием.

Дифференциальный метод – метод измерения, при котором измеряемая величина сравнивается с однородной величиной, имеющей известное значение, незначительно отличающее от значения измеряемой величины, и при которой измеряется разность между этими величинами.

Например, измерение длины сравнением с образцовой мерой на компараторе – средстве сравнения, предназначенном для сличения мер однородных величин.

Дифференциальный метод измерений наиболее эффективен тогда, когда практическое значение имеет отклонение измеряемой величины от некоторого номинального значения (отклонение действительного линейного размера от номинального, уход частоты и т. д.).

Метод измерений замещением – метод сравнения с мерой, в которой измеряемую величину замещают мерой с известным значением величины, например, взвешивание с поочередным помещением измеряемой массы и гирь на одну и ту же чашку весов).

Метод измерений дополнением – метод сравнения с мерой, в котором значение измеряемой величины дополняется мерой этой же величины с таким расчетом, чтобы на прибор сравнения воздействовала их сумма, равная заранее заданному значению.

Метод противопоставления –метод сравнения с мерой, в котором измеряемая величина, воспроизводимая мерой, одновременно действует на прибор сравнения, с помощью которого устанавливается соотношение между этими величинами.

Например, измерение массы на равноплечих весах с помещением измеряемой массы и уравновешивающих ее гирь на двух чашках весов, сличение мер с помощью компаратора, где основой метода является выработка сигнала о наличии разности размеров сравниваемых величин.

Метод совпадений -метод сравнения с мерой, в которой разность между измеряемой величиной и величиной, воспроизводимой мерой, измеряют, используя совпадение отметок шкал или периодических сигналов.

Например, измерение длины с помощью штангенциркуля с нониусом, когда наблюдают совпадение отметок на шкалах штангенциркуля и нониуса, измерение частоты вращения с помощью стробоскопа, когда положение какой либо отметки на вращающемся объекте совмещают с отметкой на невращающейся части этого объекта при определенной частоте вспышек стробоскопа.

Контактный метод измерений – метод измерений, при котором чувствительный элемент прибора (измерительные поверхности прибора или инструмента) приводятся в контакт с объектом измерения.

Например, измерение температуры рабочего тела термопарой, измерение диаметра детали штангенциркулем.

Бесконтактный метод измерений – метод измерений, основанный на том, что чувствительный элемент СИ не приводится в контакт с объектом измерения.

Например, измерения расстояния до объекта с помощью радиолокатора, измерение линейных размеров деталей с фотоэлектрическим измерительным прибором.

1.7 Средства измерений

Средство измерения (СИ) – техническое средство, предназначенное для измерений, имеющее нормированные метрологические характеристики, воспроизводящее и (или) хранящее единицу ФВ, размер которой принимают неизменным (в пределах установленной погрешности) в течение известного интервала времени.

Средства измерений многообразны. Однако для этого множества можно выделить некоторые общие признаки, присущие всем средствам измерений независимо от области применения (рисунок 2).

По роли, выполняемой в системе обеспечения единства измерений, средства измерений делят на метрологическиеи рабочие.

Метрологические СИ предназначены для метрологических целей - воспроизведения единицы и (или) ее хранения или передачи размера единицы рабочим СИ.

Рабочие СИ – СИ, предназначенные для измерений, не связанных с передачей размера единицы другим СИ.

По отношению к измеряемой ФВ СИ подразделяются на основные и вспомогательные.

Основные СИ – СИ той ФВ, значение которой необходимо получить в соответствии с измерительной задачей.

Вспомогательные СИ–СИ той ФВ, влияние которой на основное СИ или объект измерений необходимо учитывать для получения результатов измерений требуемой точности.

Эти СИ применяют для контроля над поддержанием значений влияющих величин в заданных пределах.

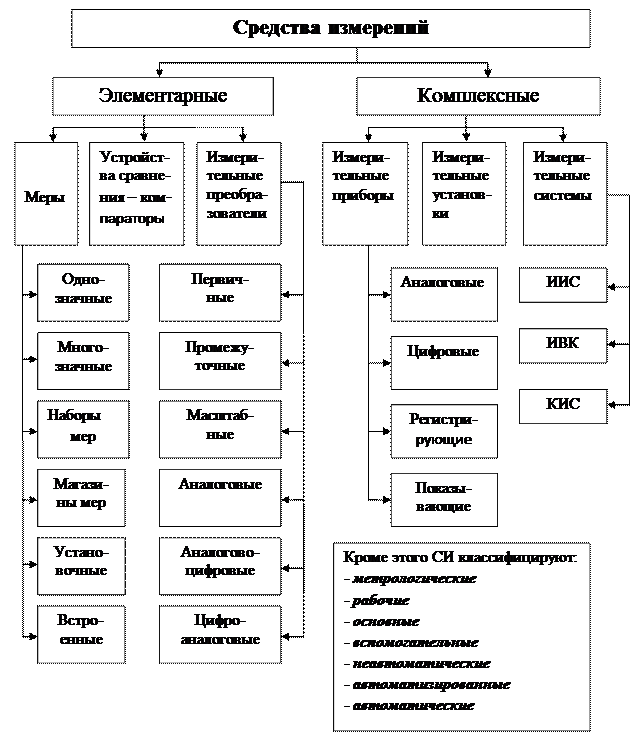
Рисунок 2 - Обобщенная классификация средств измерений

По уровню автоматизации все СИ делят на неавтоматические(имеется в виду обычный прибор, например, рычажный микрометр), автоматическиеи автоматизированные.