С помощью эквивалентных преобразований СДНФ

Элементы алгебры логики

20) Пусть нам требуется выбрать набор логических элементов, с помощью которого можно построить любую сколь угодно сложную схему.

Набор называется функционально-полным если с помощью элементов, содержащихся в наборе, можно построить сколь угодно сложную схему. Логическим элементом называется простейшая логическая схема, заданная законом функционирования, т.е. каждый логический элемент описывается с помощью функции.

Система переключательных функций называется функционально полной, если с помощью функций, входящих в данную систему, применяя операцию суперпозиции и подстановки, можно реализовать любую сколь угодно сложную переключательную функцию.

16) Представление булевой функции в алгебре Жегалкина называется полиномом Жегалкина.

Полином Жегалкина — полином(многочлен) над 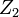, то есть полином с коэффициентами вида 0 и 1, где в качестве произведения берется конъюнкция, а в качестве сложения исключающее или. Полином был предложен в1927 году И. И. Жегалкиным в качестве удобного средства для представления функций булевой логики.

Полином Жегалкина представляет собой сумму по модулю два (операция Исключающее ИЛИ) произведений неинвертированных переменных, а также (если необходимо) константы 1. Формально полином Жегалкина можно представить в виде

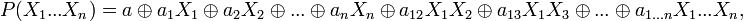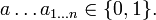Примеры полиномов Жегалкина:

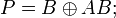
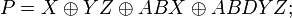
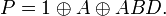
Представление функции в виде полинома Жегалкина

С помощью эквивалентных преобразований ДНФ

По сравнению с ДНФ в полиноме Жегалкина отсутствуют операции ИЛИ и НЕ. Таким образом, полином Жегалкина можно получить из ДНФ, выразив операции ИЛИ и НЕ через операции сложение по модулю два, и константу 1. Для этого применяются следующие соотношения:

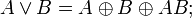
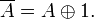
Ниже приведён пример преобразования ДНФ в полином Жегалкина:

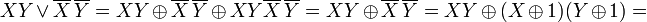
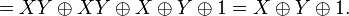
При преобразованиях использованы соотношения:

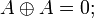
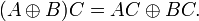
С помощью эквивалентных преобразований СДНФ

СДНФ обладает тем свойством, что при любых значениях входных переменных в единицу обращается не более одного члена выражения. Для таких выражений операция дизъюнкции эквивалентна операции сложение по модулю два.

При преобразовании СДНФ в полином Жегалкина, достаточно заменить все дизъюнкции на операции сложение по модулю два и избавиться от инверсий при помощи эквивалентного преобразования

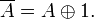
17) В алгебре Жегалкина роль совершенных форм булевых функций играют полиномы специального типа, называемые каноническими полиномами.

Каноническим полиномом называется конечная сумма по модулю два таких попарно различных произведений переменных, что в одном и том же произведении никакая переменная не встречается более одного раза.

Разложение булевых функций в канонический полином Жегалкина
Интерес к разложению булевых функций в канонический полином Жегалкина объясняется прежде всего тем, что такое представление реализуемых функций является основой для синтеза логи­ческих схем в базисе элементов И и СЛОЖЕНИЕ по МОДУЛЮ ДВА.
Определение.Полином булевой функции F, в слагаемые которого все переменные F входят только без отрица­ния или только с отрицанием, называется монотонно-поляризован­ным. Причем в первом случае полином функции F называется поло­жительно-поляризованный и обозначается через P(F), а во втором случае - отрицательно-поляризованным и обозначается через Q(F). Полином P(F) иначе называется каноническим полиномом Жегалкина.
Например, для булевой функции, заданной вектором значений таблицы истинности w(F)=(00100111) полиномы P(F) и Q(F) имеют вид:

,

.
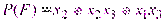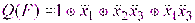Отметим некоторые свойства монотонно-поляризованных поли­номов P(F) и Q(F) булевой функции :
1. Полиномы P(F) и Q(F) являются для булевой функции F единственными.
2. Полиномы P(F) и Q(F) имеют степень n тогда и только тогда, когда

таблица истинности функции F содержит нечетное число единиц.
3. Число слагаемых полинома P(F) (Q(F)) четно тогда и только тогда, когда

(соответственно ).
Основным достоинством представления булевых функций в виде канонического поли­нома Жегалкина является то, что в этом представлении любая булева функция задается с помощью всего двух логических операций: конъюнкции и сложения по модулю два, что сокращает набор различных элементов для синтеза логи­ческих схем.

22)Теорема о функциональной полноте.

Система переключательных функций называется функционально полной, если с помощью функций, входящих в эту систему, применяя операции суперпозиции и подстановки, можно получить любую, сколь угодно сложную переключательную функцию.

Теорема о функциональной полноте. Для того чтобы система переключательных функций была функционально полной, необходимо и достаточно, чтобы эта система включала:

· хотя бы одну переключательную функцию, не со­храняющую нуль;

· хотя бы одну переключательную функцию, не со­храняющую единицу;

· хотя бы одну нелинейную переключательную функцию:

· хотя бы одну немонотонную переключательную функцию;

· хотя бы одну несамодвойственную переключатель­ную функцию.

21) Набор функций называется полным, если его замыкание совпадает со всеми логическими функциями. Иначе говоря, полный набор – это множество таких функций, через которые можно выразить все остальные булевы функции.

Неизбыточный полный набор функций называется базисом (“неизбыточный” означает, что если какую-то функцию удалить из набора, то этот набор перестанет быть полным).

Конъюнкция, дизъюнкция и отрицание являются полным набором, но не являются базисом, так как это набор избыточен, поскольку с помощью правил де Моргана можно удалить конъюнкцию или дизъюнкцию. Любую функцию можно представить в виде полинома Жегалкина. Ясно, что функции конъюнкция, сложение по модулю 2 и константы 0 и 1 являются полным набором, но эти четыре функции также не являются базисом, поскольку 1+1=0, и поэтому константу 0 можно исключить из полного набора (для построения полиномов Жегалкина константа 0 необходима, поскольку выражение “1+1” не является полиномом Жегалкина).

Легко видеть, что одним из способов проверки полноты какого-то набора К является проверка того, что через функции из этого набора выражаются функции другого полного набора (можно проверить, что через функции из К можно выразить конъюнкцию и отрицание или дизъюнкцию и отрицание.

По теореме Поста, чтобы система булевых функций была полной, надо, чтобы в ней существовали:

1. Хотя бы одна функция, не сохраняющая 0.

2. Хотя бы одна функция, не сохраняющая 1.

3. Хотя бы одна нелинейная функция.

4. Хотя бы одна немонотонная функция.

5. Хотя бы одна несамодвойственная функция.

Этому требованию отвечает система функций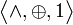

Классы поста:

Замкнутый класс в теории булевых функций — такое множество 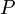функций алгебры логики, замыкание которого относительно операции суперпозиции совпадает с ним самим: 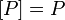. Другими словами, любая функция, которую можно выразить формулой с использованием функций множества 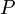, снова входит в это же множество.

В 1941 году Эмиль Пост представил полное описание системы замкнутых классов, называемое также решеткой Поста.

Свойства замыкания функции с переменными

1. Любое множество является подмножеством своего замыкания: .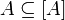

2. Замыкание подмножества является подмножеством замыкания: .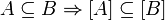
Следует заметить, что из строгого вложения множеств следует лишь нестрогое вложение их замыканий: .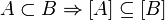

3. Многократное применение операции замыкания эквивалентно однократному: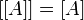

Примеры замкнутых классов

Множество 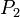всех возможных булевых функций замкнуто.

Особо важны для теории булевых функций следующие замкнутые классы, называемые предполными классами:

§ Класс 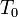функций, сохраняющих константу 0:
.

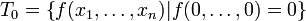§ Класс 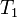функций, сохраняющих константу 1:
.

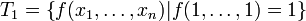§ Класс 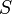самодвойственных функций:
.

§ Класс 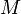монотонных функций:
.

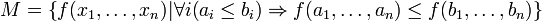§ Класс 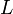линейных функций:

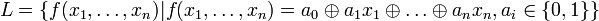
19) Алгебра Жегалкина

Булевы функции с операциями умножения и сложения по модулю 2 образуют алгебру Жегалкина.

Множество булевых функций, заданный в базисе Жегалкина S4={⊕,&,1} называется алгеброй Жегалкина.

Аксиомы алгебры Жегалкина:

1. Операции с константами: A× 1 º A; A× 0 º 0; A Å 0 º A.

2. Идемпотентность: A× A º A; A Å A º 0.

3. Коммутативность: A× B º B× A; A Å B º B Å A.

4. Ассоциативность: (A Å B) Å C º AÅ (B Å C); (A× B)× C º A× (B× C).

5. Дистрибутивность: A× (B Å C) º A× B Å A× C.

Можно перейти от алгебры Буля к алгебре Жегалкина, используя следующие соотношения: A Å 1 º ` A; AÚ B=A Å B Å A× B.

И наоборот, от алгебры Жегалкина к алгебре Буля: A Å B =` A× BÚ A× ` B

.