Тема 2.1. Решение задач линейной алгебры в пакете Mathcad (базовая часть).

Цели и задачи. Изучить основные приемы работы в пакете Mathcad, освоить операции с векторами и матрицами, научиться решать системы линейных алгебраических уравнений (СЛАУ), записанные в матричной форме.

Справочный материал.

Для присвоения значений переменным или функциям в пакете Mathcad используют символ := (двоеточие и равно), который создает в рабочем документе область определения переменной или функции. Данный символ вводится либо через панель инструментов Калькулятор , либо нажатием комбинации клавиш Shift ; (точка с запятой) в английской раскладке клавиатуры. Символ = (равно) позволяет получить числовой результат вычисления. В более поздних версиях пакета эти два символа можно совмещать в одной области.

Нумерация элементов векторов и матриц по умолчанию ведется с нуля. Более привычную нумерацию (с единицы) в рабочем документе можно установить через присвоение специальной системной переменной ORIGIN значения 1 (ORIGIN:=1). Данная область вводится перед началом работы с матричными данными. Аналогичный результат можно получить, изменив параметр ORIGIN в меню Параметры документа.

Вычисления в пакете Mathcad производятся в порядке расположения областей - слева направо и сверху вниз. Начинающему пользователю лучше всего располагать данные в документе вертикально. При вводе данных также требуется следить за тем, чтобы данные не разрывались (в рабочем документе каждая область обводится прямоугольной рамкой). Вид курсора указывает на тип области: вертикальная красная черта возникает в текстовых областях (комментариях), в вычисляемых же областях курсор имеет вид уголка синего цвета.

При редактировании формул неоднократные нажатия на клавишу пробел позволяют выделить часть выражения, к которой применяется вводимая операция. Будьте внимательны – в некоторых случаях нажатие на пробел может изменить тип области (из вычисляемой области сделать текстовую), в этом случае изменится цвет курсора.

Для именования переменных лучше использовать английскую раскладку клавиатуры. Некоторые имена зарезервированы (имеют специальное назначение) и при вводе подчеркиваются волнистой зеленой линией, их использование в других целях может привести к возникновению ошибок (но не обязательно). Кроме того, имена чувствительны к регистру (А и а – разные переменные).

Иногда при вычислениях возникает ошибка, текст которой высвечивается на экране (чаще всего - "Эта переменная не определена"). Для исправления данной ошибки требуется перед областью вычислений определить значение неизвестной переменной (если этого не было сделано ранее), либо передвинуть область ее определения чуть выше места возникновения ошибки.

Для выполнения различных действий над векторами и матрицами (вставка матрицы , индекс 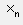, транспонирование 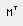, обращение 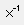, выделение столбца 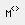, определитель и т.п.) используют панель инструментов Матрица (см. рис. 16).

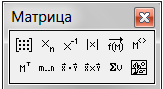
Рис. 16. Панель инструментов Матрица.

Более подробно данную тему можно изучить в [6].

Примеры задач и образцы их решения.

Задача 2.1.1.По заданным матрицам

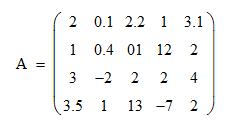
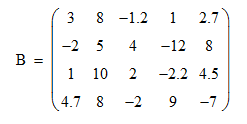
найти:

a) транспонированные матрицы ;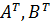

б) сумму матриц ;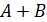

в) произведение матрицы на число 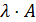, где ;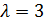

г) произведение матриц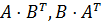

Решение.

Фрагмент рабочего документа Mathcad (версия 15.0) с решением задачи 2.1.1 представлен на рис. 17:

Рис. 17. Фрагмент документа Mathcad с решением задачи 2.1.1.

Задача 2.1.2. Произвести с матрицей А (см. задачу 2.1.1) следующие действия:

а) умножая на индикаторный вектор-строку (матрицу специального вида), выделить 1-й столбец и 2-ю строку;

б) вычислить суммы элементов 2-й строки и 1-го столбца;

в) переставить местами 1 и 3 строки, 2 и 4 столбцы.

Решение.

Фрагмент рабочего документа Mathcad (версия 15.0) с решением задачи 2.1.2 представлен на рис. 18.1 и 18.2.

Рис. 18.1. Фрагмент документа Mathcad с решением задачи 2.1.2.

Рис. 18.2. Фрагмент документа Mathcad с решением задачи 2.1.2.

Задача 2.1.3. Исследовать СЛАУ, заданную в матричном виде ( 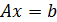), и, если решение существует, найти его по методу Крамера. Выполнить проверку найденного решения подстановкой.

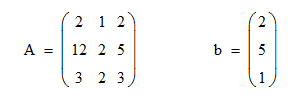
Решение.

Исходная СЛАУ является определенной (число уравнений равно числу неизвестных) и неоднородной (свободные коэффициенты в векторе b отличны от нуля). При выполнении этих условий можно вычислить определитель матрицы А, составленной из коэффициентов при неизвестных. В том случае, если он отличен от нуля, существует единственное решение такой системы.

В Mathcad 15.0 определитель можно вычислить через операцию определитель 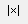панели Матрица.

По методу Крамера для поиска решения неоднородной СЛАУ используют вспомогательные матрицы, в которых каждый из столбцов исходной матрицы А поочередно заменяется на вектор свободных коэффициентов b. Количество вспомогательных матриц равно числу неизвестных системы. Значения неизвестных определяются как отношение определителей вспомогательных матриц и исходной матрицы А.

Найденное решение, как правило, обязательно должно быть проверено подстановкой в исходную систему.

Фрагмент рабочего документа Mathcad (версия 15.0) с решением задачи 2.1.3 представлен на рис.19.

Рис. 19. Фрагмент документа Mathcad с решением задачи 2.1.3.

Индивидуальные варианты задач по Теме 2.1 "Решение задач линейной алгебры в пакете MathCad".

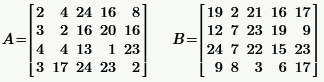
Задача 2.1.1.По заданным матрицам A и B найти:

a) транспонированные матрицы ;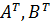

б) сумму матриц ;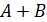

в) произведение матрицы на число 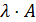, где ;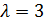

г) произведение матриц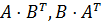

№	A, B	№	A, B

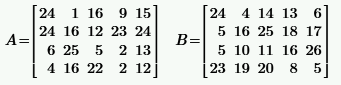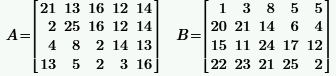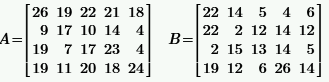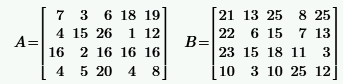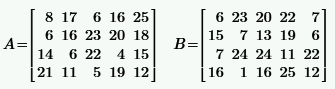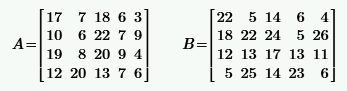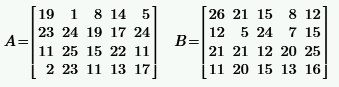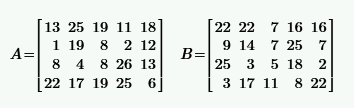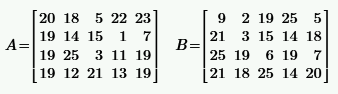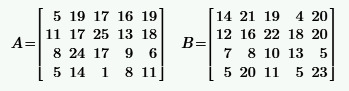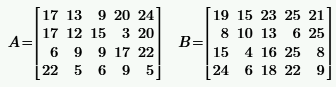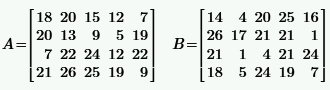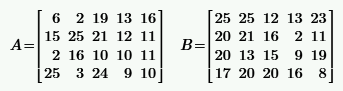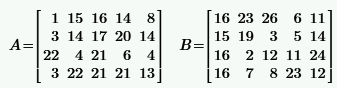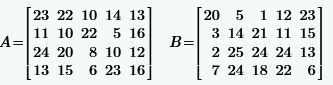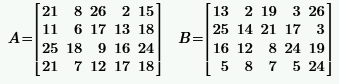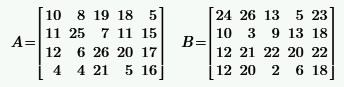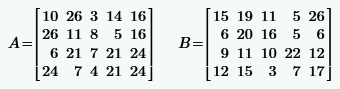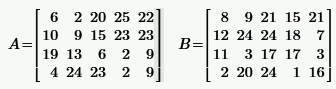Задача 2.1.2. Произвести с матрицей А следующие действия:

а) умножая на индикаторный вектор-строку (матрицу специального вида), выделить i-ю строку и j-й столбец;

б) вычислить суммы элементов i-й строки и j-го столбца;

в) переставить местами i-ю и k-ю строки, j-й и m-й столбцы.

№	A	i	j	k	m	№	A	i	j	k	m

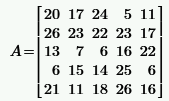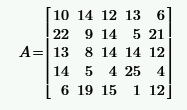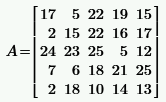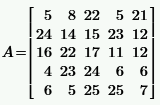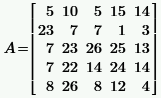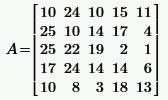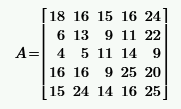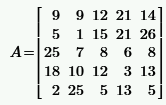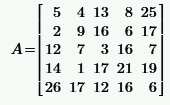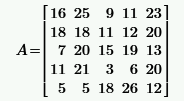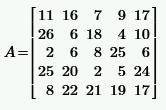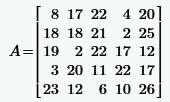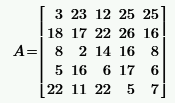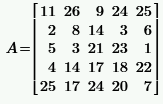Задача 2.1.3.Исследовать неоднородную СЛАУ, заданную в матричном виде ( 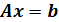), и, если решение существует, найти его по методу Крамера. Выполнить проверку найденного решения подстановкой.