Понятия знака и алфавита можно отнести только к дискретным сообщениям.

5.

Изм.

Лист

№ докум.

Подпись

Дата

Лист

21

КР 15.02.07 09 00 00 ПЗ

Разраб.

Синякина Г.Е. МММММММММММММММммухамедшиной.

Провер.

Тулинцева Л.Н.

Реценз.

Н. Контр.

Утверд.

Монтаж, наладка и эксплуатация САУ

Лит.

Листов

72

СПбГЭУПТ 332-з

Логический элемент функция НЕ, ИЛИ, И.

Современная вычислительная техника строится на основе цифровых микросхем. При этом сами цифровые микросхемы реализуются на базе простейших логических функций:

"НЕ" — функция инвертирования;

"И" — функция логического умножения;

"ИЛИ" — функция логического суммирования.

Поэтому прежде чем приступить к изучению основ вычислительной техники рассмотрим особенности реализации логических функций на базе цифровых микросхем.

· Логическая функция инвертирования «НЕ»

Простейшим логическим элементом является инвертор, который просто изменяет значение входного сигнала на прямо противоположное значение. Функция инвертирования входного сигнала, реализуемая цифровым инвертором, записывается в следующем виде:

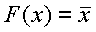
где черта над входным значением цифрового сигнала обозначает изменение его на противоположное. То же самое действие можно записать при помощи таблицы истинности, приведённой в таблице 1. Так как входной параметр у логической функции инвертирования один, то ее таблица истинности состоит только из двух строк.

In Out

0 1

1 0

Таблица 1. Таблица истинности функции логического инвертирования

В качестве логического инвертора можно использовать обычный транзисторный усилитель с транзистором, включенном по схеме с общим эмиттером или истоком. Схема, выполненная на биполярном n-p-n транзисторе, позволяющая реализовать функцию логического инвертирования приведена на рисунке 1.

Изм.

Лист

№ докум.

Подпись

Дата

Лист

22

КР 15.02.07 09 00 00 ПЗ

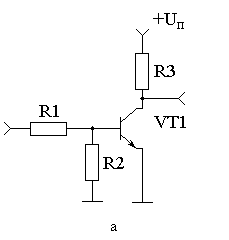
Рисунок 1. Схема, позволяющая реализовать функцию логического инвертирования

Схемы логических инверторов могут обладать различным временем распространения цифрового сигнала и могут работать на различные виды нагрузки. Они могут быть выполнены на одном или на нескольких транзисторах, но независимо от схемы и её параметров они осуществляют одну и ту же логическую функцию. Для того чтобы особенности включения транзисторов не затеняли выполняемую логическую функцию, были введены специальные обозначения для цифровых микросхем — условно-графические обозначения. Условно-графическое изображение логического инвертора приведено на рисунке 2.

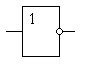
Рисунок 2. Условно-графическое изображение логического инвертора

· Логическая функция «И» (конъюнкция)

Следующей простейшей логической функцией, на основе которой реализуются элементы вычислительной техники является операция логического умножения "И". Логическая функция "И" обычно записывается следующим образом:

F(x1, x2) = x1 ∧ x2

где символ ∧ обозначает функцию логического умножения. Эта же функция может быть записана несколькими способами:

F(x1,x2) = x1^x2 = x1·x2 = x1&x2.

То же самое действие можно записать при помощи таблицы истинности, приведённой в таблице 2. В формуле, приведенной выше, использовано два аргумента. Поэтому элемент, выполняющий эту функцию имеет два входа. Такая логическая функция обозначается "2И". Для нее таблица истинности будет состоять из четырех строк (2²= 4).

Таблица 2. Таблица истинности логической функции "2И"

In1 In2 Out

0 0 0

0 1 0

1 0 0

1 1 1

Изм.

Лист

№ докум.

Подпись

Дата

Лист

23

КР 15.02.07 09 00 00 ПЗ

Проще всего понять как работает логический элемент"2И", реализующий логическую функцию умножения, при помощи схемы, построенной на идеализированных ключах с электронным управлением, как это показано на рисунке 3. В этой схеме ток будет протекать только тогда, когда оба ключа будут замкнуты, следовательно, единичный уровень напряжения на выходе данной схемы появится только при двух логических единицах на входах идеализированных электронных ключей.

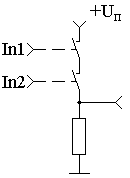
Рисунок 3. Принципиальная схема, реализующая логическую функцию "2И"

Условно-графическое изображение электронной схемы, выполняющей логическую функцию "2И", на принципиальных схемах цифровых и вычислительных устройств приведено на рисунке 4, и с этого момента схемы, выполняющие логическую функцию "И" будут приводиться именно в таком виде. Это изображение не зависит от конкретной принципиальной схемы устройства, реализующей функцию логического умножения.

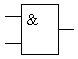
Рисунок 4. Условно-графическое изображение схемы, выполняющей логическую функцию "2И"

· Логическая функция «ИЛИ» (дизъюнкция)

Следующей функцией, широко использующейся при реализации вычислительных устройств является операция логического сложения "ИЛИ", которую часто называют дизъюнкцией. Эта операция двух выражений записывается следующим образом:

F(x1, x2) = x1 ∨ x2

где символ ∨ обозначает функцию логического сложения. Иногда эта же логическая функция записывается в другом виде:

F(x1, x2) = x1 ∨ x2 = x1 + x2 = x1 | x2

То же самое действие можно записать при помощи таблицы истинности, приведённой в таблице 3. В формуле, приведенной выше, использовано два аргумента. Поэтому схема, выполняющая функцию логического суммирования имеет два входа. Такой элемент обозначается "2ИЛИ". Для логической функции "2ИЛИ" таблица истинности будет состоять из четырех строк (2² = 4).

Таблица 3. Таблица истинности схемы, выполняющей логическую функцию "2ИЛИ"

In1 In2 Out

0 0 0

0 1 1

1 0 1

1 1 1

Как и в случае, рассмотренном для схемы логического умножения, воспользуемся для реализации схемы "2ИЛИ" идеализированными электронными ключами. На этот раз соединим ключи параллельно. Схема, реализующая логическую функцию "2ИЛИ" (см. таблицу истинности 3), приведена на рисунке 5. Как видно из приведённой схемы уровень логической единицы появится на её выходе, как только будет замкнут любой из ключей, то есть схема реализует таблицу истинности, приведённую в таблице 3.

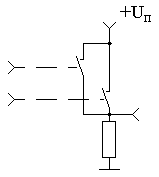
Рисунок 5. Принципиальная схема, реализующая логическую функцию "2ИЛИ"

Изм.

Лист

№ докум.

Подпись

Дата

Лист

24

КР 15.02.07 09 00 00 ПЗ

Так как функция логического суммирования может быть реализована различными принципиальными схемами, то для обозначения этой функции на принципиальных схемах используется специальный символ '1', как это показано на рисунке 6.

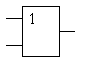
Рисунок 6. Условно-графическое изображение схемы, выполняющей логическую функцию "2ИЛИ"

6.

Изм.

Лист

№ докум.

Подпись

Дата

Лист

25

КР 15.02.07 09 00 00 ПЗ

Разраб.

Синякина Г.Е. МММММММММММММММммухамедшиной.

Провер.

Тулинцева Л.Н.

Реценз.

Н. Контр.

Утверд.

Монтаж, наладка и эксплуатация САУ

Лит.

Листов

72

СПбГЭУПТ 332-з

Карты Карно

Карта Карно — графический способ минимизации переключательных (булевых) функций, обеспечивающий относительную простоту работы с большими выражениями и устранение потенциальных гонок. Представляет собой операции попарного неполного склеивания и элементарного поглощения. Карты Карно рассматриваются как перестроенная соответствующим образом таблица истинности функции. Карты Карно можно рассматривать как определенную плоскую развертку n-мерного булева куба.

Карты Карно были изобретены в 1952 Эдвардом В. Вейчем и усовершенствованы в 1953 Морисом Карно, физиком из «Bell Labs», и были призваны помочь упростить цифровые электронные схемы.

В карту Карно булевы переменные передаются из таблицы истинности и упорядочиваются с помощью кода Грея, в котором каждое следующее число отличается от предыдущего только одним разрядом.

Основным методом минимизации логических функций, представленных в виде СДНФ или СКНФ является операция попарного неполного склеивания и элементарного поглощения. Операция попарного склеивания осуществляется между двумя термами (членами), содержащими одинаковые переменные, вхождения которых (прямые и инверсные) совпадают для всех переменных, кроме одной. В этом случае все переменные, кроме одной, можно вынести за скобки, а оставшиеся в скобках прямое и инверсное вхождение одной переменной подвергнуть склейке. Например:

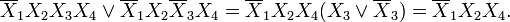
Возможность поглощения следует из очевидных равенств

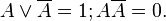
Таким образом, главной задачей при минимизации СДНФ и СКНФ является поиск термов, пригодных к склейке с последующим поглощением, что для больших форм может оказаться достаточно сложной задачей. Карты Карно предоставляют наглядный способ отыскания таких термов.

Как известно, булевы функции N переменных, представленные в виде СДНФ или СКНФ могут иметь в своём составе 2N различных термов. Все эти члены составляют некоторую структуру, топологически эквивалентную N–мерному кубу, причём любые два терма, соединённые ребром, пригодны для склейки и поглощения.

На рисунке изображена простая таблица истинности для функции из двух переменных, соответствующий этой таблице 2-мерный куб (квадрат), а также 2-мерный куб с обозначением членов СДНФ и эквивалентная таблица для группировки термов:

Изм.

Лист

№ докум.

Подпись

Дата

Лист

26

КР 15.02.07 09 00 00 ПЗ

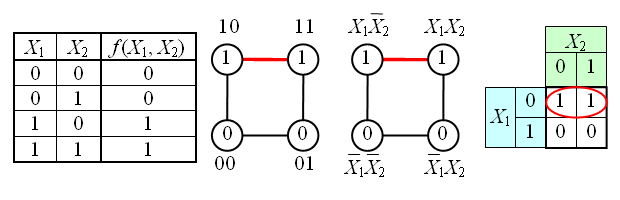
В случае функции трёх переменных приходится иметь дело с трёхмерным кубом. Это сложнее и менее наглядно, но технически возможно. На рисунке в качестве примера показана таблица истинности для булевой функции трёх переменных и соответствующий ей куб.

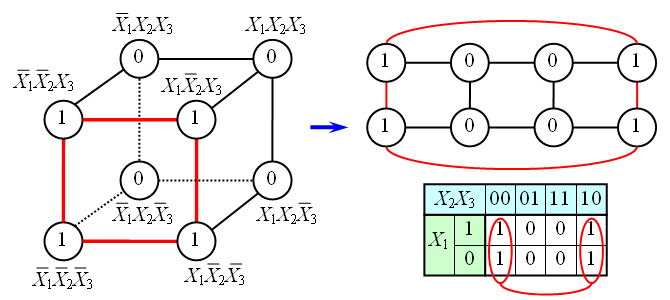
Как видно из рисунка, для трёхмерного случая возможны более сложные конфигурации термов. Например, четыре терма, принадлежащие одной грани куба, объединяются в один терм с поглощением двух переменных:

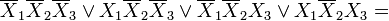
В общем случае можно сказать, что 2K термов, принадлежащие одной K–мерной грани гиперкуба, склеиваются в один терм, при этом поглощаются K переменных.

Для упрощения работы с булевыми функциями большого числа переменных был предложен следующий удобный приём. Куб, представляющий собой структуру термов, разворачивается на плоскость как показано на рисунке. Таким образом появляется возможность представлять булевы функции с числом переменных больше двух в виде плоской таблицы. При этом следует помнить, что порядок кодов термов в таблице (00 01 11 10) не соответствует порядку следования двоичных чисел, а клетки, находящиеся в крайних столбцах таблицы, соседствуют между собой.

Изм.

Лист

№ докум.

Подпись

Дата

Лист

27

КР 15.02.07 09 00 00 ПЗ

Аналогичным образом можно работать с функциями четырёх, пяти и более переменных. Примеры таблиц для N=4 и N=5 приведены на рисунке. Для этих таблиц следует помнить, что соседними являются клетки, находящиеся в соответственных клетках крайних столбцов и соответственных клетках верхней и нижней строки. Для таблиц 5 и более переменных нужно учитывать также, что квадраты 4х4 виртуально находятся друг над другом в третьем измерении, поэтому соответственные клетки двух соседних квадратов 4х4 являются сосоедними, и соответствующие им термы можно склеивать.

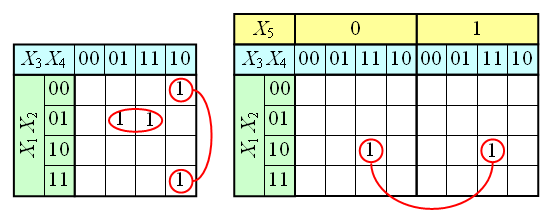
Карта Карно может быть составлена для любого количества переменных, однако удобно работать при количестве переменных не более пяти. По сути Карта Карно — это таблица истинности составленная в 2-х мерном виде. Благодаря использованию кода Грея в ней верхняя строка является соседней с нижней, а правый столбец соседний с левым, т.о. вся Карта Карно сворачивается в фигуру тор (бублик). На пересечении строки и столбца проставляется соответствующее значение из таблицы истинности. После того как Карта заполнена, можно приступать к минимизации.

Если необходимо получить минимальную ДНФ, то в Карте рассматриваем только те клетки которые содержат единицы, если нужна КНФ, то рассматриваем те клетки которые содержат нули. Сама минимизация производится по следующим правилам (на примере ДНФ):

· Объединяем смежные клетки содержащие единицы в область, так чтобы одна область содержала 2n (n целое число = 0…\infty) клеток(помним про то что крайние строки и столбцы являются соседними между собой), в области не должно находиться клеток содержащих нули;

· Область должна располагаться симметрично оси(ей) (оси располагаются через каждые четыре клетки);

· Не смежные области расположенные симметрично оси(ей) могут объединяться в одну;

· Область должна быть как можно больше, а кол-во областей как можно меньше;

· Области могут пересекаться;

· Возможно несколько вариантов накрытия.

Изм.

Лист

№ докум.

Подпись

Дата

Лист

28

КР 15.02.07 09 00 00 ПЗ

Далее берём первую область и смотрим какие переменные не меняются в пределах этой области, выписываем конъюнкцию этих переменных, если неменяющаяся переменная нулевая, проставляем над ней инверсию. Берём следующую область, выполняем то же самое что и для первой, и т. д. для всех областей. Конъюнкции областей объединяем дизъюнкцией.

Для КНФ всё то же самое, только рассматриваем клетки с нулями, не меняющиеся переменные в пределах одной области объединяем в дизъюнкции (инверсии проставляем над единичными переменными), а дизъюнкции областей объединяем в конъюнкцию. На этом минимизация считается законченной. Так для Карты Карно на рис.1 выражение в формате ДНФ будет иметь вид:

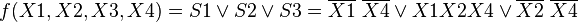
В формате КНФ:

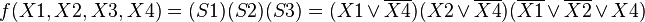
Изм.

Лист

№ докум.

Подпись

Дата

Лист

29

КР 15.02.07 09 00 00 ПЗ

Разраб.

Синякина Г.Е. МММММММММММММММммухамедшиной.

Провер.

Тулинцева Л.Н.

Реценз.

Н. Контр.

Утверд.

Монтаж, наладка и эксплуатация САУ

Лит.

Листов

72

СПбГЭУПТ 332-з

7. Системы счисления

Система счисления – это способ представления чисел и соответствующие ему правила действия над числами. Разнообразные системы счисления, которые существовали ранее и существуют теперь, можно разделить на позиционные (десятичная, двоичная, троичная и т.д.) и непозиционные (римская ). Знаки, которые используются при записи чисел, называются цифрами.

В непозиционных системахсчисления от положения цифры в записи числа не зависит величина, которую она обозначает.

Примером непозиционной системы счисления является римская система (римские цифры). В римской системе в качестве цифр используются латинские буквы:

I V X L C D M

1 5 10 50 100 500 1000

Пример 1:

Число CCXXXII складывается из двух сотен, трех десятков и двух единиц и равно 232.

В римских числах цифры записываются слева направо в порядке убывания. В таком случае их значения складываются. Если же слева записана меньшая цифра, а справа - большая, то их значения вычитаются.

Пример 2:

VI=5+1=6, а IV=5-1=4

Пример 3:

MCMXCVIII =1000+ (1000-100) + (-10+100) +5+1+1+1=1998

В позиционных системах счисления величина, обозначаемая цифрой в записи числа, зависит от ее позиции. Количество используемых цифр называется основанием позиционной системы счисления.

Система счисления, применяемая в современной математике, является позиционной десятичной системой. Ее основание равно десяти, т.к. запись любых чисел производится с помощью десяти цифр:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

Позиционный характер этой системы легко понять при наличии любого многозначного числа. Например, в числе 333первая тройка означает три сотни, вторая - три десятка,
а третья – три единицы.

Изм.

Лист

№ докум.

Подпись

Дата

Лист

30

КР 15.02.07 09 00 00 ПЗ

Для записи чисел в позиционной системе счисления с основанием n нужно иметь алфавит из n цифр. Обычно для этого при n < 10 используют n первых арабских цифр, а при n > 10 к десяти арабским цифрам добавляют буквы. Вот примеры алфавитов нескольких систем:

Основание	Название	Алфавит
n=2	двоичная	0 1
n=3	троичная	0 1 2
n=8	восьмеричная	0 1 2 3 4 5 6 7
n=16	шестнадцатеричная	0 1 2 3 4 5 6 7 8 9 A B C D E F

Если требуется указать основание системы, к которой относится число, то оно приписывается нижним индексом к этому числу. Например:

В системе счисления с основанием q (q-ичная система счисления) единицами разрядов служат последовательные степени числа q. q единиц какого-либо разряда образуют единицу следующего разряда. Для записи числа в q-ичной системе счисления требуется q различных знаков (цифр), изображающих числа 0,1,…,q-1. запись числа q в q-ичной системе счисления имеет вид 10.

Правила перехода

Из десятичной СС в двоичную СС:

1. Разделить десятичное число на 2. Получится частное и остаток.

2. Частное опять разделить на 2. Получится частное и остаток.

3. Выполнять деление до тех пор, пока последнее частное не станет меньшим 2.

4. Записать последнее частное и все остатки в обратном порядке. Полученное число и будет двоичной записью исходного десятичного числа.

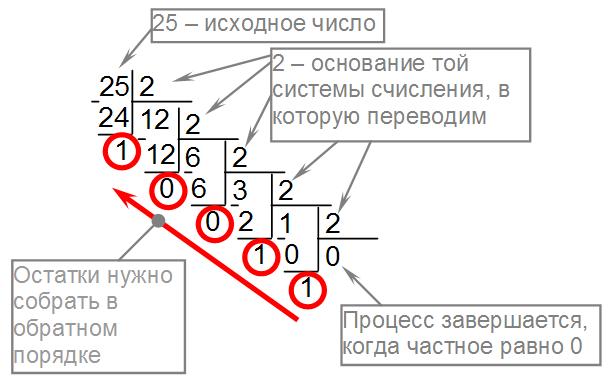
Правило перехода из двоичной системы счисления в десятичную:

Для перехода из двоичной системы счисления в десятичную, необходимо двоичное число представить в виде суммы степеней двойки и найти ее десятичное значение.

Пример:

111012 =1*2 +1*2³+1*2² +0*2¹ +1*2˚ == 16 +8+4 +0+1=2910

Правило перехода из десятичной системы счисления в восьмеричную:

Изм.

Лист

№ докум.

Подпись

Дата

Лист

31

КР 15.02.07 09 00 00 ПЗ

1. Разделить десятичное число на 8. Получится частное и остаток.

2. Частное опять разделить на 8. Получится частное и остаток.

3. Выполнять деление до тех пор, пока последнее частное не станет меньшим 8.

4. Записать последнее частное и все остатки в обратном порядке. Полученное число и будет восьмеричной записью исходного десятичного числа.

Правило перехода из восьмеричной системы счисления в десятичную:

Для перехода из восьмеричной системы счисления в десятичную необходимо восьмеричное число представить в виде суммы степеней восьмерки и найти ее десятичное значение.

2158 =2*8² +1*8¹+5*8˚ =128 +8 +5 =14110

Те же правила и для шестнадцатеричной системы.

Изм.

Лист

№ докум.

Подпись

Дата

Лист

32

КР 15.02.07 09 00 00 ПЗ

Разраб.

Синякина Г.Е. МММММММММММММММммухамедшиной.

Провер.

Тулинцева Л.Н.

Реценз.

Н. Контр.

Утверд.

Монтаж, наладка и эксплуатация САУ

Лит.

Листов

72

СПбГЭУПТ 332-з

9.Технические характеристики
цифровых вычислительных машин

Цифровая вычислительная машина (ЦВМ) — вычислительная машина, преобразующая величины, представленные в виде набора цифр (чисел). Простейшие преобразования чисел, известные с древнейших времён, — это арифметические действия (сложение и вычитание). Но арифметические операции — лишь частный случай преобразований величин, заданных в цифровой форме, и в современных ЦВМ они составляют лишь небольшую часть всего набора операций, которые машина выполняет над числами.

Существуют различные классификации компьютерной техники:

· по этапам развития (по поколениям);

· по архитектуре;

· по производительности;

· по условиям эксплуатации;

· по количеству процессоров;

· по потребительским свойствам и т.д.

Четких границ между классами компьютеров не существует. По мере совершенствования структур и технологии производства, появляются новые классы компьютеров, границы существующих классов существенно изменяются.

Поколения компьютеров.

Технические характеристики и особенности классов

Деление компьютерной техники на поколения — весьма условная, нестрогая классификация вычислительных систем по степени развития аппаратных и программных средств, а также способов общения с компьютером.

Идея делить машины на поколения вызвана к жизни тем, что за время короткой истории своего развития компьютерная техника проделала большую эволюцию как в смысле элементной базы (лампы, транзисторы, микросхемы и др.), так и в смысле изменения её структуры, появления новых возможностей, расширения областей применения и характера использования.

Характеристика Поколения Первое Второе Третье Четвертое Годы применения 1946-1960 1950-1964 1964-1970 1970-1990-e Основной элемент Электронная лампа Транзистор Интегральная схема Большая интегральная схема Количество ЭВМ в мире, шт Сотни Тысячи Сотни тысяч Десятки миллионов Размеры Очень большие (ENIAC, UNIVAC, EDSAC) Значительно меньшие Миникомпьютеры Микрокомпьютеры Быстротдействие 1 (условно) 1 000 100 000 Носитель информации Перфорированная лента Магнитный диск, м. лента Диск Гибкий диск Объем ОП 64 Кб 512 Кб 16 Мб Более 16 Мб

Изм.

Лист

№ докум.

Подпись

Дата

Лист

33

КР 15.02.07 09 00 00 ПЗ

ЭВМ пятого поколения

ЭВМ пятого поколения – это программа в Японии по развитию вычислительной техники и искусственного интеллекта. Основным их качеством должен быть высокий интеллектуальный уровень. Машины пятого поколения – это реализованный искусственный интеллект. В них будет возможным ввод с голоса, голосовое общение, машинное "зрение", машинное "осязание". Многое уже практически сделано в этом направлении.

ЭВМ пятого поколения должны удовлетворять следующим качественно новым функциональным требованиям:

1. Обеспечивать простоту применения ЭВМ путем эффективных систем ввода-вывода информации, диалоговой обработки информации с использованием естественных языков, возможности обучаемости, ассоциативных построений и логических выводов (интеллектуализация ЭВМ);

2. Упростить процесс создания программных средств путем автоматизации синтеза

Изм.

Лист

№ докум.

Подпись

Дата

Лист

34

КР 15.02.07 09 00 00 ПЗ

программ по спецификациям исходных требований на естественных языках; усовершенствовать инструментальные средства разработчиков;

3. Улучшить основные характеристики и эксплуатационные качества ЭВМ, обеспечить их разнообразие и высокую адаптируемость к приложениям.

Пятое поколение компьютеров это название «плана действий» по развитию IT-индустрии. И не смотря на то, что пятое поколение базируется на микропроцессорах как и четвертое т.е. у них общая элементная база. А именно по этому критерию разделяют компьютеры на поколения. Тем не менее сегодняшние компьютеры относят к пятому поколению.

Классификация компьютеров

по архитектуре. Архитектура ЭВМ

Архитектура ЭВМ включает в себя как структуру, отражающую состав ПК, так и программно – математическое обеспечение. Структура ЭВМ — совокупность элементов и связей между ними. Основным принципом построения всех современных ЭВМ является программное управление.

Основы учения об архитектуре вычислительных машин были заложены Джон фон Нейманом. Совокупность этих принципов породила классическую (фон-неймановскую) архитектуру ЭВМ.

Фон Нейман не только выдвинул основополагающие принципы логического устройства ЭВМ, но и предложил ее структуру, представленную на рисунке.

Положения фон Неймана:

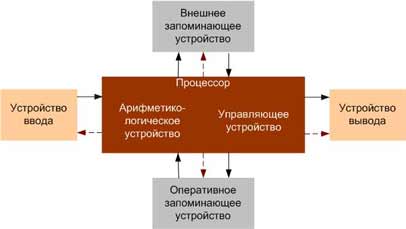
ü Компьютер состоит из нескольких основных устройств (арифметико-логическое устройство, управляющее устройство, память, внешняя память, устройства ввода и вывода)

ü Арифметико-логическое устройство – выполняет логические и арифметические действия, необходимые для переработки информации, хранящейся в памяти

ü Управляющее устройство – обеспечивает управление и контроль всех устройств компьютера (управляющие сигналы указаны пунктирными стрелками)

ü Данные, которые хранятся в запоминающем устройстве, представлены в двоичной форме

ü Программа, которая задает работу компьютера, и данные хранятся в одном и том же запоминающем устройстве

ü Для ввода и вывода информации используются устройства ввода и вывода

ü Один из важнейших принципов – принцип хранимой программы требует, чтобы программа закладывалась в память машины так же, как в нее закладывается исходная информация.

ü Арифметико-логическое устройство и устройство управления в современных компьютерах образуют процессор ЭВМ. Процессор, который состоит из одной или нескольких больших интегральных схем называется микропроцессором или микропроцессорным комплектом.

ü Процессор – функциональная часть ЭВМ, выполняющая основные операции по обработке данных и управлению работой других блоков. Процессор является преобразователем информации, поступающей из памяти и внешних устройств.

ü

Изм.

Лист

№ докум.

Подпись

Дата

Лист

35

КР 15.02.07 09 00 00 ПЗ

Запоминающие устройства обеспечивают хранение исходных и промежуточных данных, результатов вычислений, а также программ. Они включают: оперативные (ОЗУ), сверхоперативные СОЗУ), постоянные (ПЗУ) и внешние (ВЗУ) запоминающие устройства.

ü Оперативные ЗУ хранят информацию, с которой компьютер работает непосредственно в данное время (резидентная часть операционной системы, прикладная программа, обрабатываемые данные). В СОЗУ хранится наиболее часто используемые процессором данные. Только та информация, которая хранится в СОЗУ и ОЗУ, непосредственно доступна процессору.

ü Внешние запоминающие устройства (накопители на магнитных дисках, например, жесткий диск или винчестер) с емкостью намного больше, чем ОЗУ, но с существенно более медленным доступом, используются для длительного хранения больших объемов информации. Например, операционная система (ОС) хранится на жестком диске, но при запуске компьютера резидентная часть ОС загружается в ОЗУ и находится там до завершения сеанса работы ПК.

ü ПЗУ (постоянные запоминающие устройства) и ППЗУ (перепрограммируемые постоянные запоминающие устройства) предназначены для постоянного хранения информации, которая записывается туда при ее изготовлении, например, ППЗУ для BIOS.

ü В качестве устройства ввода информации служит, например, клавиатура. В качестве устройства вывода – дисплей, принтер и т.д.

Изм.

Лист

№ докум.

Подпись

Дата

Лист

36

КР 15.02.07 09 00 00 ПЗ

В построенной по схеме фон Неймана ЭВМ происходит последовательное считывание команд из памяти и их выполнение. Номер (адрес) очередной ячейки памяти, из которой будет извлечена следующая команда программы, указывается специальным устройством – счетчиком команд в устройстве управления.

Общеизвестно что компьютеры имеют разную внутреннюю структуру, элементы и разные виды связей между ними.

Например по архитектуре можно классифицировать компьютеры следующим образом:

· компьютеры с шинной архитектурой

· компьютеры с канальной архитектурой

Технические характеристики

Микропроцессор. Самым главным элементом в компьютере является микропроцессор – небольшая электронная схема, выполняющая все вычисления и обработку информации. Одинаковые модели микропроцессоров могут иметь разную тактовую частоту – чем выше тактовая частота, тем выше производительность и цена микропроцессора.

Оперативная память. Из нее процессор берет программы и исходные данные для обработки, в нее он записывает полученные результаты. (128, 256 ОЗУ)

Электронные платы. Каждая плата представляет собой плоский кусок пластика, на котором укреплены электронные компоненты (микросхемы, конденсаторы и т.д.) и различные разъемы.

Материнская плата. Самой большой электронной платой в ком­пьютере является системная, или материнская, плата. На ней обычно располагаются ос­новной микропроцессор, оперативная па­мять, кэш-память, шина (или шины) и ВIOS. Контроллеры. Электронные схемы, управляющие различными уст­ройствами компьютера, называются контроллерами.

Платы контроллеров. В большинстве компью­теров некоторые контроллеры располага­ются на отдельных электронных платах – платах контроллеров.

Изм.

Лист

№ докум.

Подпись

Дата

Лист

37

КР 15.02.07 09 00 00 ПЗ

Шины. При вставке в разъем материнской платы контроллер подключается к шине – магистрали передачи данных между оперативной памятью и контроллерами.

Контроллеры портов ввода-вывода. Часто этот контроллер интегрирован на материнской плате. Контроллер портов ввода-вывода соединен кабелями с разъемами на задней стенке компьютера, через которые к компьютеру подключаются принтер, мышь и некоторые другие устройства. Порты ввода-вывода бывают следующих типов: параллельные (LPT1 – LPT4), последовательные (обозначаемые СОМ1-СОМЗ), игровой порт – к его разъему

Разъемы шины USB. В некоторых новых компьютерах имеются разъемы универсальной последовательной шины USB.

Накопители на жестком диске (винчестеры) предназначены для постоянного хранения информации, используемой при работе с компьютером и программ операционной системы. Из всех устройств хранения данных жесткие диски обеспечивают.

Дисководы, видео карта, звуковая карта.