Некоторые определения из теории множеств
Пермский Государственный Технический Университет
Кафедра Информационных технологий и автоматизированных систем
Викентьева О. Л.
Математическая логика и теория алгоритмов
Конспект лекций
для студентов специальностей АСУ, ЭВТ, КЗИ
Пермь, 2007 г.
Введение
Математическая логика - это современный вид формальной логики. Логика – это наука правильно рассуждать, имея какие-то утверждения, истинность которых проверена, например, на опыте. С помощью утверждений можно придти к новому утверждению, которое также может оказаться истинным.
Исходное утверждение называется посылкой, результирующее утверждение – заключением.
Пример 1.
П1: Все люди смертны.
П2. Сократ – человек.
З: Сократ смертен.
Пример 2.
П1: Все граждане России имеют право на образование.
П2: Иванов – гражданин России.
З: Иванов имеет право на образование.
Оба эти вывода имеют одну и ту же форму:
Все А есть В;
С есть А;
Следовательно, С есть В.
В этих рассуждениях нам не интересна истинность или ложность отдельных посылок. Нам важно знать вытекает ли истинность заключения из истинности посылок.
Таким образом, основная задача логики – это формализация правильных способов рассуждения. Если при этом применяется математический аппарат, то такую логику можно назвать математической.
Тема 1. Логика высказываний
Понятие высказывания
Рассмотрим логику высказываний, которая лежит в основе всех других разделов математической логики (МЛ) и необходима для их понимания.
Логика высказываний строится также как и другие математические теории. В качестве основных понятий берется некоторый класс объектов, а также некоторые свойства, отношения и операции над этими объектами.
Основным объектом логики высказываний служат простые высказывания. Высказывание – это предложение, о котором можно сказать истинно оно или ложно.
Примеры.
1. Число 100 делится на 5.
2. Число 3 больше числа 5.
3. Луна больше Земли.
4. Сегодня светит солнце.
5. Вечером мы пойдем в кино.
Из простых высказываний с помощью некоторого числа логических операций можно построить сложные высказывания.
1. Число 100 делится на 5 и число 100 делится на 10.
2. Неверно, что 3 больше 5.
3. Сегодня мы пойдем в кино или мы пойдем в театр.
При изучении логики высказываний не обращают внимание на содержание простых высказываний, а интересуются только их истинностью или ложностью.
Сложные высказывания, получаемые из простых, будут также истинными или ложными. Их истинность или ложность будет зависеть от истинности образующих их простых высказываний.
Логические операции
Для изучения логических операций введем следующую систему обозначений:
· простые высказывания будем обозначать буквами a, b, c, …, x, y ,z;
· значения истинности будем обозначать 1 – истинно, 0 – ложно.
Действия логических операций будем представлять в виде таблиц истинности.
1. Отрицание или инверсия (Ø – НЕ)
Пример.
а: 7 делится на 5 без остатка.
Øа: Неверно, что 7 делится на 5 без остатка.
| а | Øа |
Эта таблица и принимается в качестве определения операции отрицания.
2. Конъюнкция ( Ù,&, ·, логическое И )
Действие операции определяется следующим образом: сложное высказывание а&b истинно только в том случае, когда оба высказывания (а и b) имеют значение истинно.
| а | b | а&b |
Примеры.
а. 6 делится на 3 без остатка (1);
b. 10 больше 5 (1);
с. 7 делится на 3 без остатка (0);
d. 3 больше 7 (0);
a&b=1
a&c=0
c&d=0
3. Дизъюнкция (Ú,+,логическое ИЛИ)
Действие операции определяется следующим образом: сложное высказывание аÚв ложно только в том случае, когда оба высказывания (а и в) ложны.
| a | b | aÚb |
Примеры.
аÚb=1
aÚc=1
cÚd=0
4. Импликация ( 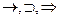 ) “если а, то b”
) “если а, то b”
Действие операции определяется следующим образом: сложное высказывание а 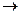 b ложно только в том случае, когда а истинно, а b – ложно.
b ложно только в том случае, когда а истинно, а b – ложно.
| a | b | a 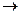 b b |
А называется антецедентом, а b – консеквентом.
5. Эквивалентность (~ 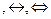 )
)
Действие операции определяется следующим образом: сложное высказывание а~b истинно, если а истинно и b истинно, или если а ложно и b ложно.
| a | b | a~b |
Эквивалентность примерно соответствует употреблению выражения «тогда и только тогда».
6. сумма по модулю два 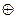
| a | b | a 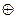 b b |
7. Штрих Шеффера ( ê, обратная конъюнкция И – НЕ)
| a | b | a ê b |
8. Стрелка Пирса ( 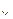 , обратная дизъюнкция ИЛИ – НЕ )
, обратная дизъюнкция ИЛИ – НЕ )
| a | b | a 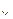 b b |
Используя эти логические операции можно строить сколь угодно сложные высказывания.
Приоритет выполнения операций:
⌐ & Ú 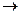 ~
~ 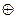 ê
ê 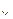
Пример: Сложное высказывание: «Если вы не пропускаете занятия и успешно занимаетесь, то Вы сдадите экзамен хорошо» можно записать следующим образом. Обозначим:
П – пропускаете занятия;
Y – успешно занимаетесь;
Х – сдадите экзамен хорошо,
тогда все высказывание запишется:
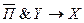
Значение истинности всего выражения будет зависеть от истинности переменных обозначающих простые высказывания.
Пример.
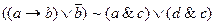
Пусть a=1, b=0, c=0, d=1.
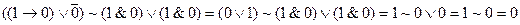
Символы ⌐ & Ú 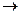 ~
~ 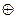 ê
ê  называются пропозициональными связками, a, b, c, … и т. д. - пропозициональными переменными. Выражение, построенное из пропозициональных переменных с помощью пропозициональных связок, называется пропозициональной формой или формулой.
называются пропозициональными связками, a, b, c, … и т. д. - пропозициональными переменными. Выражение, построенное из пропозициональных переменных с помощью пропозициональных связок, называется пропозициональной формой или формулой.
Булевы функции
Некоторые определения из теории множеств
Множество – фундаментальное неопределяемое понятие. Множество – это совокупность объектов, которые, с одной стороны, различны и отличимы друг от друга, а с другой стороны воспринимаются как единое целое.
Пусть А и В – два множества.
<a,b> - упорядоченная пара, где первый элемент 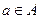 , а второй элемент
, а второй элемент 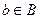 .
.
Декартово произведение 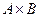 - это множество пар
- это множество пар
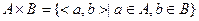
Бинарным отношением f из множества А в множество В называется подмножество 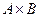 :
:
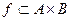 .
.
Функция - это такое отношение, что из 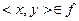 и
и 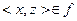 следует, что x=z, т. е. функциональность – это однозначность.
следует, что x=z, т. е. функциональность – это однозначность.
Пример.
А={1,2,3,4,5}
B={1,4,9,16,25}
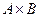 ={<1,1>, <1,4>, <1,9>, <1,16>, <1,25>, <2,1>, <2,4>, <2,9>, <2,16>, <2,25>,….<3,9>, …. ,<4,16>,…..<5,25>}
={<1,1>, <1,4>, <1,9>, <1,16>, <1,25>, <2,1>, <2,4>, <2,9>, <2,16>, <2,25>,….<3,9>, …. ,<4,16>,…..<5,25>}
f={<1,1>, <2,4>, <3,9>, <4,16>, <5,25>} – это функция, где b=a2.
Булевы функции
Функция 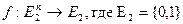 называется функцией алгебры логики.
называется функцией алгебры логики.
y=f(x1,x2) – бинарная функция,
y=f(x1,x2,…., xn) – n- арная функция.
Пример.
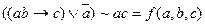
Т. о. каждое элементарное высказывание может принимать значение либо 0, либо 1. Каждому набору значений a, b, c соответствует одно значение всего сложного высказывания (0 или 1).
Булеву функцию от n переменных можно задать таблицей истинности
| x1 | ….. | xn-1 | xn | f(x1, …,xn) |
Переменные, которые принимают значения 0 или 1 называются булевыми переменными.
Некоторые функции всегда принимают значение 1 (на любом наборе переменных). Такие функции называются тавтологиями. Некоторые функции всегда принимают значение 0 (на любом наборе переменных). Такие функции называются противоречиями.
Формулы
Пусть 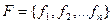 - множество булевых функций. Формулой над F называется выражение
- множество булевых функций. Формулой над F называется выражение 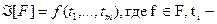 либо переменная, либо формула над F.
либо переменная, либо формула над F.
F называется базисом формулы, f – главной (внешней) операцией, ti – подформулами.
Всякой формуле 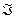 однозначно соответствует некоторая функция f. Это соответствие задается алгоритмом интерпретации, который позволяет вычислить значение функции при заданных значениях переменных.
однозначно соответствует некоторая функция f. Это соответствие задается алгоритмом интерпретации, который позволяет вычислить значение функции при заданных значениях переменных.
Зная таблицы истинности для функций базиса можно вычислить таблицу той функции, которую реализует данная формула.
Примеры.
1. 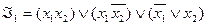
| x1 | x2 | x1 x2 | 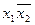 | 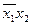 | 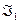 |
Функция 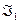 реализует дизъюнкцию на базисе
реализует дизъюнкцию на базисе 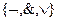 .
.
2. 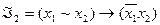
| x1 | x2 | x1~ x2 | 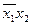 | 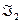 |
Функция 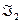 реализует дизъюнкцию на базисе
реализует дизъюнкцию на базисе 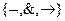 .
.
Таким образом каждая формула определяет некоторую логическую функцию, которую можно представить в виде таблицы истинности для этой формулы. Если в формуле имеется n переменных, то возможны 2n различных истинностных значений для этой формулы. Следовательно, таблица истинности будет иметь 2n строк.
Равносильные формулы
Одна функция может иметь множество реализаций над данным базисом (т. е. ее можно записать с помощью различных формул). Формулы, реализующие одну и ту же функцию, называют равносильными. Обозначают 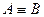 .
.
Пример.
Пусть 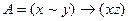 ,
, 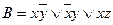 .
.
Доказать, что 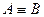 .
.
Равносильность двух формул можно доказать с помощью таблиц истинности. Формулы равносильны, если их значения истинности совпадают на любом наборе значений истинности, входящих в них переменных.
Таблица истинности для формулы А.
| x | y | z | x~y | xz | A |
Таблица истинности для формулы B.
| x | y | z | 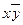 | 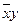 | xz | B |
Тот факт, что равносильность формул логики высказываний можно проверить непосредственно, связан с тем, что переменные, входящие в формулу могут принимать конечное число значений (2n).
Но, если в формуле большое количество переменных, то вычисление всех значений истинности для формулы становится очень трудоемкой задачей.
Равносильность формул логики высказываний аналогична тождествам элементарной алгебры, известным из средней школы. Но тождественное равенство алгебраических формул нельзя проверить простым перебором значений, т. к. число возможных значений переменных неограниченно, следовательно, доказательство равносильности никогда не закончится. В элементарной алгебре тождественные равенства формул устанавливаются с помощью небольшого числа основных тождеств – законов, связывающих между собой арифметические операции.
Для логики имеют место следующие равносильности (рассмотрим только формулы, которые содержат знаки 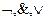 ):
):
1. Коммутативный
АÚВ 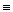 ВÚА АВ=ВА
ВÚА АВ=ВА
2. Ассоциативный
АÚ(ВÚС) 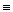 (АÚВ) ÚС А(ВС)=(АВ)С
(АÚВ) ÚС А(ВС)=(АВ)С
3. Дистрибутивный
АÚ(ВС) 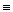 (АÚВ)(АÚС) А(ВÚС)=АВÚАС
(АÚВ)(АÚС) А(ВÚС)=АВÚАС
4. Идемпотентности
АÚА 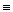 А А·А
А А·А 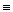 А
А
5. Поглощения
АÚАВ 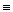 А А(АÚВ)
А А(АÚВ) 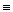 А
А
6. АÚ0 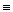 А А· 0 = 0
А А· 0 = 0
7. АÚ1=1 А·1=А
8. АÚ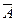 =1 А×
=1 А× 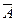 =0
=0
9. Закон де Моргана
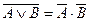
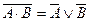
10. 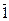 = 0
= 0 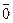 = 1
= 1
11 Двойное отрицание
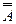 = А
= А
12. А 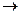 В
В 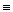
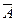 ÚВ
ÚВ
13 А~В=А·ВÚ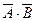
14 А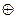 В=
В= 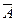 ·ВÚА·
·ВÚА· 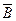
15. А çВ = АÚВ = А·В
16. А ¯ В = 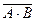 =
= 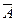 Ú
Ú 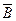
Подстановка и замена
Если в формулу 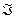 входит переменная х, то это можно обозначить как
входит переменная х, то это можно обозначить как 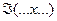 . Если в формулу входит подформула
. Если в формулу входит подформула 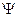 , то обозначим это как
, то обозначим это как 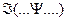 .
.
Вместо подформулы или переменной можно подставить другую формулу или переменную. В результате получится новая правильно построенная формула.
Если подстановка производится вместо всех вхождений заменяемой переменной или подформулы, то результат обозначим:
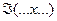 {
{ 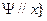 , т. е. все вхождения переменной х заменяем на подформулу
, т. е. все вхождения переменной х заменяем на подформулу 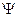 .
.
Если подстановка производится вместо некоторых вхождений, то результат обозначим
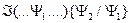 , т. е. первое вхождение
, т. е. первое вхождение 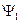 заменяем на
заменяем на 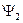 .
.
Примеры.
1. Замена всех вхождений переменной х
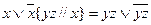
2. Замена всех вхождений подформулы 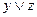
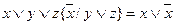
3. Замена первого вхождения переменной х
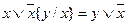
4. Замена первого вхождения подформулы 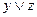
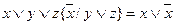
· Правило подстановки. Если в равносильных формулах вместо всех вхождений некоторой переменной x подставить одну и ту же формулу, то получатся равносильные формулы.
· Правило замены. Если в формуле заменить некоторую подформулу на равносильную, то получится равносильная формула.
