Тема 5. ЭЛЕМЕНТЫ ТЕОРИИ АЛГОРИТМОВ

Понятие алгоритма

Для устранения нечеткости интуитивного понятия алгоритма были предложены точные математические модели алгоритма, например такие, как машина Тьюринга, система рекурсивных функций, нормальные алгоритмы Маркова. С помощью этих моделей алгоритма доказана алгоритмическая неразрешимость ряда важных задач математики и вычислительной техники.

Алгоритмическая неразрешимость некоторой задачи означает, что не существует общего алгоритма, решающего любую задачу рассматриваемого класса, но для отдельных подклассов алгоритмически неразрешимой задачи может существовать алгоритм.

Формализация понятия алгоритма необходима как для доказательства отсутствия алгоритма решения какой-либо задачи, так и для изучения работы вычислительных устройств, реализующих алгоритм.

В разделе рассмотрено одно из формальных описаний интуитивного понятия алгоритма – машина Тьюринга.

Машина Тьюринга

Машина Тьюринга – абстрактная машина, математическая модель идеализированного вычислительного устройства. Машина Тьюринга полностью определяется:

а) внешним алфавитом A = {a₀, a₁,... a_n}, где a₀ – символ пустой ячейки;

б) алфавитом внутренних состояний Q = {q₀, q₁,...q_m}, где q₀ – состояние остановки: попав в него машина прекращает работу; q₁– начальное состояние: в этом состоянии машина начинает работать;

в) программой, т.е. совокупностью команд T(i,j) (i=1, …, m; j=0,1,…, n),каждая из которых имеет вид: a_jq_i®a_rSq_k, где S – предписание лентопротяжному механизму машины (сдвиг), S = L, если сдвиг влево, S = R, если сдвиг вправо,
S = C, если каретка остается на месте. Условие однозначности требует, чтобы для любого j и любого i имелась только одна команда указанного вида.

Машина Тьюринга состоит из ленты и управляющего устройства (УУ) со считывающей и записывающей головкой (кареткой) (рис. 5.1).

Рис. 5.1. Схема машины Тьюринга

Лента жестко закреплена слева и бесконечна справа. Иногда считают, что лента не ограничена справа и слева. Лента разделена на ячейки, которые нумеруются натуральными числами. В каждую ячейку ленты заносятся символы внешнего алфавита машины Тьюринга. Головка может передвигаться вдоль ленты влево и вправо. Когда она неподвижна, то стоит против некоторой ячейки ленты; говорят, что головка обозревает эту ячейку. За единицу времени (шаг) головка может сдвинуться на одну ячейку влево или вправо. Головка может распознать содержимое обозреваемой ячейки, заносить символ внешнего алфавита в текущую ячейку и стирать содержимое текущей ячейки (записывать туда пробел). Управляющее устройство может находиться в одном из множества дискретных состояний.

Словом называется последовательность P = a_i1, a_i2, … , a_is символов, записанных в ячейках ленты, где a_i1 – символ, находящийся в самой левой непустой ячейке, а a_is – символ, находящийся в самой правой непустой ячейке. Количество символов в слове называется длиной слова.

Пусть в некоторый момент времени t на ленте записано слово P, управляющее устройство находится в состоянии q_i, а каретка – напротив символа a_im слова P. Конфигурацией машины в момент времени t называется последовательность K = a_i1, … , a_{i(m – 1)}, q_i, a_im … , a_is. Конфигурации в начале и в конце работы называют соответственно начальной и заключительной.

Пример 5.1.

Машина с внешним алфавитом A = {1, a}, алфавитом внутренних состояний Q = {q₁, q₂} и программой

1q₁®1Rq₁,

aq₁®1R q₁,

из любой начальной конфигурации будет работать бесконечно, заполняя единицами всю ленту вправо от начальной точки.

Порядок работы машины Тьюринга задается в виде таблицы. В каждый столбец верхней строчки заносятся символы внутреннего алфавита, в каждую строчку первого столбца – символы внешнего алфавита. В ячейках на пересечении других столбцов и строчек помещаются команды.

Если на пересечении какой-либо строки и какого-либо столбца получим пустую клетку, то это означает, что в данном внутреннем состоянии данный символ встретиться не может.

Таблица 5.1

A Q	q0	q1	…	qi	qn
a0 a1 … aj … am				arSqk

Формат команды: aSq, где a – новое содержимое текущей ячейки (символ внешнего алфавита, который заносится в ячейку); S – команда лентопротяжному механизму (влево, вправо, стоп); q – новое внутреннее состояние машины Тьюринга. Работа машины на основании заданной программы происходит следующим образом.

Предположим, что в данный момент времени машина Тьюринга находится во внутреннем состоянии q_i, а в обозреваемой головкой ячейке ленты находится символ a_j. Тогда машина переходит к выполнению команды a_rSq_k в ячейке, на пересечении столбца q_i и строки a_j:

1) в текущую ячейку ленты заносится новый символ a_r ;

2) происходит сдвиг головки влево (S = L), или сдвиг головки вправо (S = R), или головка остается неподвижной (S = C);

3) машина переходит в новое внутреннее состояние q_k.

Возможные случаи останова машины Тьюринга:

1) в ходе выполнения программы машина дойдет до выполнения команды остановки; программа считается выполненной (результативная остановка);

2) машина никогда не останавливается, происходит зацикливание.

Данные машины Тьюринга – это слова во внешнем алфавите ленты. На ленте записывается и исходные данные, и конечный результат. На ленте могут быть записаны последовательности слов. Между словами ставится специальный символ – разделитель, пробел или, например, символ *. Натуральное число a представляется словом 1…1= 1^a, состоящим из a единиц. Например, числу 3 соответствует слово 111.

Пример 5.2.

Построить машину Тьюринга, которая производит сложение двух натуральных чисел a и b. Сложить два числа a и b – значит слово 1^a * 1^b преобразовать в слово 1 ^a+b. Это можно сделать, удалив в записи a*b символ разделителя * и сдвинув первое слагаемое ко второму. Такая машина может быть задана таблицей 5.2.

Внешний алфавит A = {1, *, _}, где * – символ разделителя, а _ – символ пустой ячейки (пробела). Множество внутренних состояний состоит из трех состояний Q = {q₀, q₁, q₂}.

Таблица 5.2

A Q	q0	q1	q2
* _	_Rq1 _Rq1	1Rq1 1Lq2 _Cq1	1Lq2   _1Rq1

Начальное и конечное состояния ленты для случая a = 5, b = 3 представлено на рис. 5.2 a и б.

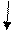a)

*

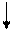б)

Рис. 5.2. Схема машины Тьюринга, выполняющей
сложение двух натуральных чисел

Задания

Постройте машину Тьюринга, которая заданное входное слово P преобразует в выходное слово R. В начальном положении обозревается крайняя левая ячейка на ленте.

Варианты индивидуальных заданий

№	P	R	№	P	R

Список литературы

1. Лавров И.А. Задачи по теории множеств, математической логике и теории алгоритмов: учеб. пособие / И.А. Лавров, Л.Л. Максимова. – М.: Наука, 1984. – 223 с.

2. Гуц А.К. Математическая логика и теория алгоритмов: учеб. пособие / А.К. Гуц. – Изд-во Либроком, 2009. – 120 с.

3. Непейвода Н.Н. Прикладная логика: учеб. пособие / Н.Н. Непейвода. – Ижевск: Изд-во Удмурского университета, 1997. – 385 с.

4. Новиков П.С. Элементы математической логики / П.С. Новиков. – М.: Наука, 1973. – 400 с.

5. Игошин В.И. Задачи и упражнения по математической логике и теории алгоритмов: учеб. пособие / В.И. Игошин. – М.: Издательский центр «Академия», 2005. – 304 с.

6. Математическая логика и теория алгоритмов: метод. указания / сост. С.А. Ка­за­ков, Н.А. Правоторова. – М.: Изд-во МГАПИ, 2002. – 45 с.

7. Кузнецов О.П. Дискретная математика для инженера / О.П. Кузнецов. – СПб.: Изд-во «Лань», 2005. – 400 с.

8. Потапов В.И. Компьютерная арифметика и алгоритмическое моделирование арифметических операций: учеб. пособие / В.И. Потапов, О.П. Шафеева. – Омск: Изд-во ОмГТУ, Гриф УМО. 2005. – 96 с.

9. Анкудинов Г.И. Математическая логика и теория алгоритмов: учеб. пособие / Г.И. Анкудинов, И.Г. Анкудинов, О.А. Петухов. – СПб.: Изд-во СЗТУ, 2003. – 104 с.

Редактор Л.И. Чигвинцева

Компьютерная верстка О.Г. Белименко

ИД № 06039 от 12.10.2001

Свод. темплан 2009 г.

Подписано в печать 11.09.09. Формат 60х84 ¹/₁₆. Отпечатано на дупликаторе.

Бумага офсетная. Усл. печ. л. 2,5. Уч.-изд. л. 2,5. Тираж 200 экз. Заказ 601.

Издательство ОмГТУ. Омск, пр. Мира, 11. Т. 23-02-12

Типография ОмГТУ