Элементы теории алгоритмов

Слово алгоритм (или алгорифм) происходит от имени арабского математика (из Хорезма Мохаммеда ибн Мусы Альхваризми (IX в.), из трактата которого Европа в XII в. познакомилась с позиционной системой счисления и с арифметическими действиями над числами в таких системах. В связи с этим и само понятие алгоритма ассоциировалось в начале с искусством счета. Постепенно понятие алгоритма деформировалось и к началу XX в. под алгоритмом стали понимать четко определенную процедуру решения некоторого класса задач. Конечно, приведенное пояснение не может служить определением понятия алгоритма. Однако, таким весьма туманным понятием алгоритма математики довольствовались вплоть до XX в., пока не появилась необходимость в доказательстве отсутствия алгоритмов для решения некоторых классов задач. Дело в том, что к началу XX в. в математике накопилось много задач алгоритмического характера не поддававшихся решению, несмотря на многочисленные усилия математиков. Примером может служить известная 10-я проблема Гильберта сформулированная им в докладе “Математические проблемы”, произнесенном в 1900 году на II Международном конгрессе математиков в Париже. Эта проблема заключалась в нахождении способа, позволяющего за конечное число операций установить, разрешимо ли произвольно заданное алгебраическое уравнение с целыми коэффициентами в целых числах или нет. Наличие таких задач зарождало у математиков идею о доказательстве отсутствия алгоритмов их решения. Результаты об отсутствии алгоритмов решения задач теми или иными ограниченными средствами к тому времени уже были. Например, было известно, что задачи трисекции угла, удвоения куба и т. д. неразрешимы с помощью циркуля и линейки. Однако теперь речь шла об отсутствии алгоритмавообще. Для решения такого рода задач необходим был новый качественный скачок в математике. А именно, нужно было дать точное определение понятия алгоритма, поскольку невозможно доказать отсутствие чего-то туманного и расплывчатого.

Задача определения алгоритма была решена в 30-х годах XX в, в ра­ботах математиков и логиков Гильберта, Гёделя, Чёрча, Клини, Поста и Тьюринга. Было дано несколько разных определений понятия алгорит­ма. При этом Гильберт, Гёдель, Чёрч и Клини подошли к понятию алго­ритма через вычислимые арифметические функции, а Пост и Тьюринг - через сведение алгоритма к элементарным преобразованиям слов в ко­нечных алфавитах.

Второй подход к определению алгоритма был использован в 40-х годах и советским математиком А. А. Марковым (1903—1979). Определенные им алгоритмы получили название нормальных алгоритмов Мар­кова.

Прежде чем дать строгое определение алгоритма, математики проанализировали известные примеры алгоритмов и выделили наиболее общие их свойства. Для выявления этих свойств рассмотрим и мы пов­нимательнее, например, хорошо известный из курса алгебры алгоритм Евклида нахождения наибольшего общего делителя двух натуральных чисел. В нем предписывается делить с остатком 1-е число на 2-е, затем 2-е на полученный (первый) остаток, затем 1-Й остаток на 2-й оста­ток и т. д. до тех пор, пока не получится остаток, равный нулю. Послед­ний, не равный нулю, остаток и будет искомым наибольшим общим де­лителем. В итоге любая пара натуральных чисел a, b преобразуется в число d, равное их наибольшему общему делителю:

(a, b)= d.

Характерными свойствами алгоритма Евклида являются:

1) массовость—алгоритм может быть применен к любой паре натуральных чисел, причем сама схема работы алгоритма не зависит от ис­ходных данных (в любом случае дели 1-е число на 2-е и т. д.);

2) дискретность-весь алгоритм можно разбить на отдельные элементарные операции (шаги алгоритма), которые могут быть занумеро­ваны натуральными числами в порядкеих выполнения;

3) детерминированность - каждый шаг алгоритма однозначно определяется его предыдущими шагами;

4) конечная определенность—исходные данные, а также результаты каждого шага алгоритма и ответ записываются в виде конечных после­довательностей символов исходного конечного алфавита.

Нетрудно видеть, что указанными свойствами обладают и другие известные нам алгоритмы, например, алгоритмы умножения целых чисел, многочленов и матриц, алгоритм Гаусса для решения систем линейных уравнений и т. д.

На примере алгоритма Евклида просматриваются не только общие черты алгоритма вообще, но и упомянутые выше два подхода к общему определению алгоритма. А именно, с одной стороны, это вычисление значений некоторой числовой функции двух переменных о. 6.. а с другой—преобразование одной последовательности символов (цифр чисел а и b, разделенных запятой) в другую последовательность (цифр числа d).

Конечно, не все алгоритмы должны иметь дело с натуральными числами, однако слова в произвольном конечном (и даже счетном) алфавите можно занумеровать натуральными числами и потому любой алгоритм можно свести к вычислению арифметической функции. Тем самым строгое определение алгоритма при первом подходе по существу сводится к нахождению какого-то строгого и конструктивного описания всех вычислимых арифметических функций. При втором подходе требуется четко определить элементарные преобразования слов и последовательности их выполнения во всех алгоритмах.

В каждом из имеющихся в настоящее время определений алгоритма, по существу, описывается некоторый класс алгоритмов и приводится обоснование того, что решение любого класса задач сводится к алгоритму из выделенного класса. Обоснование, как правило, заключается в построении большого числа примеров и в доказательстве замкнутости выделенного класса алгоритмов относительно различного рода комбинаций алгоритмов (композиции, объединения, разветвления и т. п.). Наиболее убедительным доводом в указанном обосновании явилось доказательство равносильности всех имеющихся определений алгоритмов. В итоге к настоящему времени в математическом мире сложилось достаточно единодушное мнение о законности имеющихся определений алгоритма. так что если доказывается отсутствие, скажем, нормального алгоритма для решения какого-либо класса задач, то говорится об отсутствии алгоритма вообще.

В данной главе мы опишем три различных определения понятия алгоритма и приведем простейшие примеры на доказательство теорем об отсутствии алгоритмов для решения некоторых задач.

В заключение отметим, что наличие алгоритмически неразрешимых задач ни в коей мере не противоречит общепризнанному положению диалектического материализма о познаваемости мира. Дело в том, что в теории алгоритмов речь идет об отсутствии общего алгоритма для решения слишком широкого (бесконечного) класса задач, а не какой-либо отдельной задачи.

НОРМАЛЬНЫЕ АЛГОРИТМЫ

Каждый нормальный алгоритм (НА) является определенным процессом преобразования слов в некотором конечном алфавите и задается набором допустимых элементарных преобразований и правилами, определяющими порядок применения этих преобразований. При этом в качестве элементарного преобразования используется замена одного вхождения подслова в слове некоторым другим (или тем же словом). Всевозможные замены для заданного НА определяются его схемой, а последовательность проведения замен – схемой и некоторыми дополнительными соглашениями. Эти соглашения одни и те же для всех НА, а потому НА, по существу, однозначно определяются алфавитом и схемой.

Определение 1. Схемой нормального алгоритма 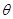в алфавите

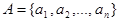
называется упорядоченная последовательность

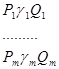(1)

слов 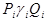в алфавит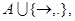е где 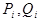- слова в алфавите 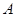, а 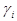есть слово 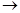или 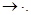При этом слово 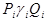схемы (1) называется ее 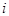-й формулой с левой частью 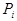и правой частью .

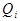Формула 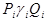называется простой, если 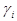есть 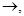и заключительной, если есть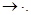

Действие НА 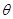на слово 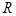в алфавите 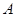описывается следующим определением.

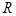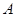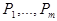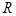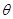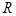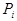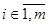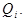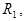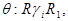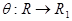Определение 2. Пусть - слово в алфавите и хотя бы одно из слов является его подсловом. Элементарным преобразованием слова по нормальному алгоритму со схемой (1) называется замена в первого вхождения слова с наименьшим номером словом Если результатом указанного элементарного преобразования является слово то пишут т. е. или .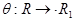

Определение 3. Говорят, что НА 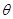в алфавите 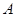применим к слову 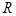в алфавите 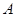и перерабатывает его в слово 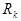, если существует конечная последовательность слов

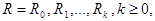(2)

в которой

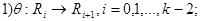
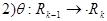или 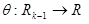и слово 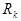не содержит подслов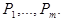

В противном случае говорят, что алгоритм 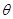не применим к слову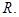

Из приведенных определений естественным образом извлекается описание процесса переработки слова 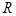по нормальному алгоритму 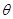(или нормальным алгоритмом 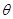). А именно, по заданному слову 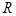НА 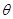строит последовательность слов. Если 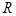не содержит подслов 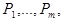то эта последовательность одноэлементна и состоит из единственного слова 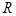. Если же 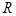содержит хотя бы одно из подслов 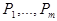, то производится его элементарное преобразование по НА 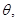в результате чего получается вполне определенное слово 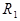. Если при переходе от 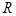к 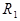использовалась заключительная формула, то искомая последовательность двухэлементная: 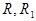. В противном случае так же, как и выше, по слову 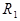строится слово 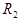и т. д. В процессе построения указанной последовательности могут представиться три различные возможности: или на каком-то шаге будет использована заключительная формула схемы алгоритма, или появится слово, не содержащее подслов 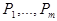, или не произойдет ни того, ни другого. В превых двух случаях мы получим конечную последовательность, последнее слово которой называется результатом применения НА к слову 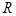и обозначают через 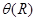. В третьем случае процесс преобразования слов по НА 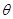будет длитться бесконечно, это и означает, что НА 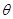не применим к .

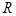Таким образом, НА 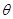в алфавите 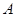задает частичное отображение множества 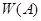всех слов в алфавите 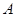в само себя. Выбирая различные схемы, мы будем получать различные НА.

Если 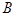- алфавит, содержащий 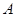, то НА в алфавите 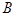называется нормальным алгоритмом над алфавитом .

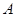Приведем примеры нормальных алгоритмов. При этом буквой 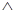будет всегда обозначаться пустое слово (в любом алфавите).

1. НА в алфавите 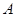со схемой

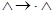
перерабатывает любое слово 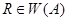в себя, причем последовательность слов, соответствующая слову 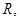имеет вид: .

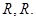2. НА со схемой

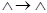
не применим ни к одному слову. Последовательность, соответствующая слову 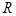будет бесконечной:

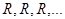
3. НА 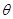в алфавите 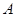со схемой

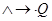
приписывает к любому слову 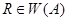слева слово :

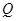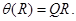
4. Построим НА 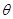, приписывающий к любому слову 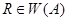справа фиксированное непустое слово 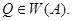Это сделать несколько сложнее, чем приписывание слова 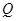слева. Для этого удобнее расширить алфавит 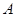, добавив к нему одну новую букву 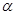, и построить искомый НА в алфавите 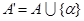(т. е. над 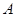). Нетрудно проверить, что нужное нам преобразование будет осуществлять НА со схемой

……………..

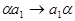
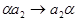
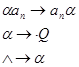
Последовательность слов, соответствующая произвольному слову 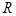в алфавите 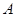, для этого НА имеет вид:

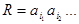
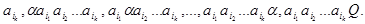
Очевидно, что то же самое преобразование слов будет осущетвлять НА, полученный из 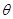любой перестановкой 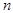формул его схемы. В связи сэтим вместо первых 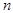формул схемы пишут просто

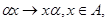
так, что вся схема запишется в виде:

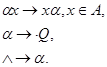
Заметим, что, выполняя свою задачу приписывания к словам из 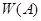справа слова 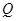, мы совсем не интересовались переработкой слов в алфавите 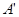, содержащих букву 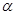. Здесь алгоритм 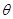будет действовать иначе. А именно, слово 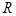в алфавите 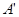, содержащее 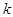вхождений буквы 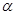, он будет перерабатывать в слово

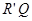
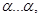где количество букв 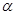будет равно ,

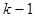где 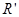получается из 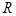удалением всех вхождений буквы 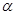(т. е. 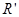есть проекция 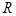в алфавит ).

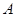5. Построим НА 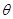, перерабатывающий любое слово 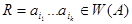в перевернутое слово 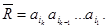Для этого добавим к 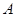две новые буквы 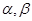и возьмем следующую схему 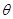в алфавите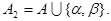

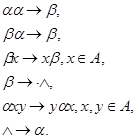
Проследите в качестве упражнения, что 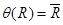для любого слова 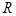в алфавите .

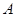Приведем еще примеры НА над числами. Условимся натуральное число 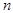записывать в виде 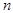вертикальных палочек.

6. НА в алфавите 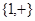со схемой

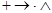
осуществляет сложение натуральных чисел.

7. НА в алфавите 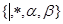со схемой

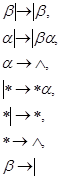
осуществляет умножение натуральных чисел.