Примеры законов распределения случайных величин.

1) Равномерное распределение. Непрерывное распределениес плотностью, постояннойна некотором участке 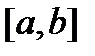и равной нулю всюду кроме этого участка, называется равномерным распределением. Из соотношения 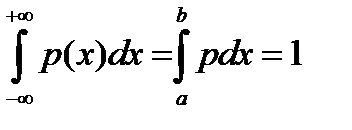имеем постоянное значение плотности на участке 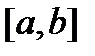: 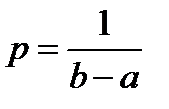. В соответствии с формулой 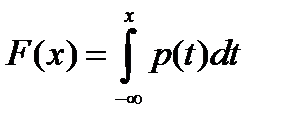имеем следующий график функции равномерного распределения: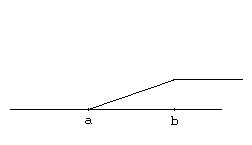

Вычислим характеристики равномерного распределения: ,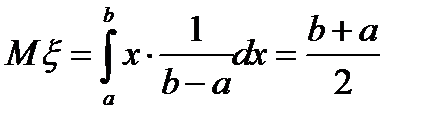

.

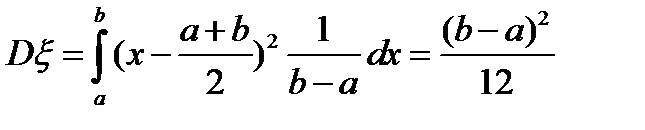2) Биномиальное распределение. Дискретная случайная величина, принимающая только целые неотрицательные значения, не большие числа 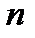, с вероятностями 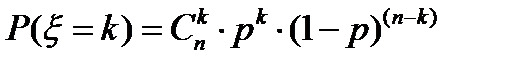, называется распределенной по биномиальному закону. Заметим, что приведенная величина фигурировала в формуле Бернулли, которая давала вероятность наступления события в 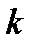опытах из 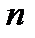, если вероятность наступления события в одном опыте равна 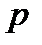. Характеристики распределения таковы: 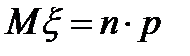, 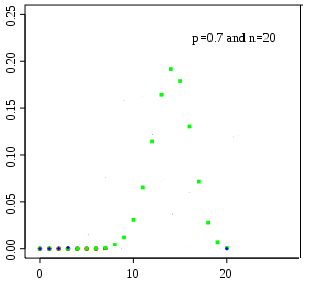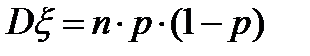. 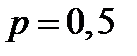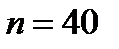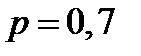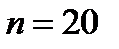На двух следующих графиках заданы законы распределения с , и с , , соответственно.

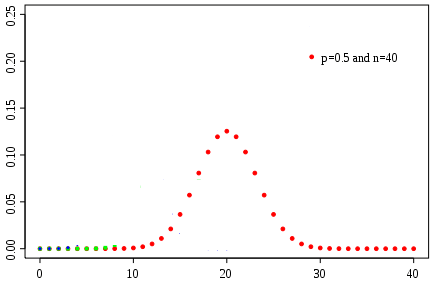
3) Нормальный закон распределения Гаусса. Этот закон распределения непрерывной случайной величины очень часто применим, поэтому остановимся на нем подробнее.

Если для дискретной величины, распределенной по биномиальному закону, построить зависимость вероятности 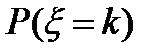от значения 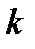, мы заметим, что с ростом 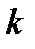при 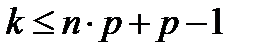вероятность монотонно возрастает, а при 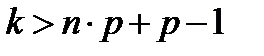с ростом 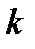вероятность монотонно убывает, достигая наибольшего значения при значениях, близких к математическому ожиданию 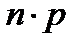. Это можно проследить на приведенных выше двух графиках законов биномиального распределения. Нечто подобное можно наблюдать и при построении подобной зависимости для дискретной величины, распределенной по закону Пуассона.

Аналогом закона распределения дискретной случайной величины в случае непрерывной случайной величины является плотность распределения. Естественно иметь такой закон распределения непрерывной случайной величины, плотность которого достигает наибольшего значения при значениях случайной величины, равных математическому ожиданию этой величины.

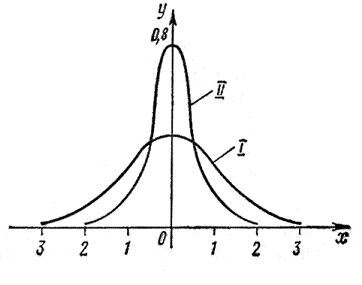
Непрерывная случайная величина называется распределенной по нормальному закону, если ее плотность вероятности равна 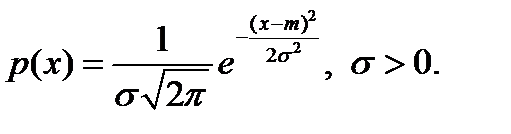График плотности распределения – кривая, симметричная относительно точки 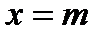, монотонно возрастающая от нуля ( 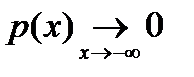) при 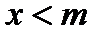и монотонно убывающая к нулю ( 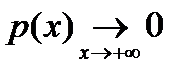) при 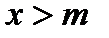. На приведенном ниже рисунке совмещены графики плотностей двух нормальных распределений. График I соответствует значениям параметров 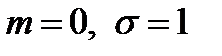, а график II – значениям параметров .

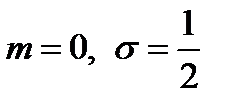Коэффициент при экспоненциальной функции подобран таким, чтобы выполнялось условие 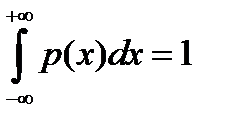. (При вычислении интеграла от плотности используется значение интеграла Эйлера-Пуассона: 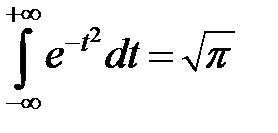). Функция распределения величины, распределенной по нормальному закону, можно задать следующим образом:

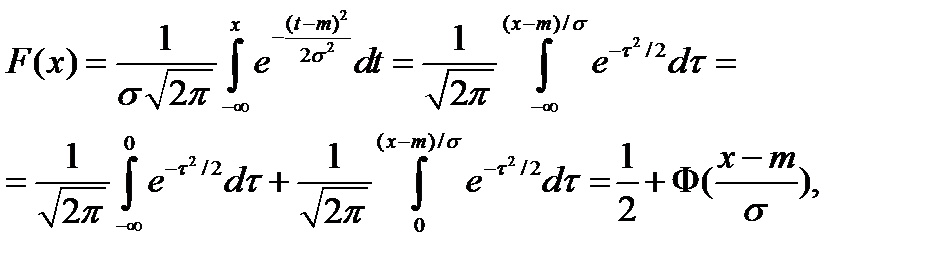
где функция 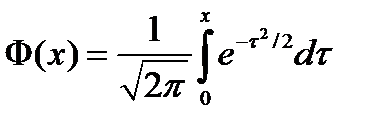называется функцией Лапласа.

Функция Лапласа задается таблично, как и многие известные функции (тригонометрические функции, экспоненциальная функция и логарифмическая функция). Это монотонно возрастающая, нечетная функция, .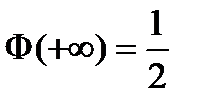

Если случайная величина имеет распределение по нормальному закону, то 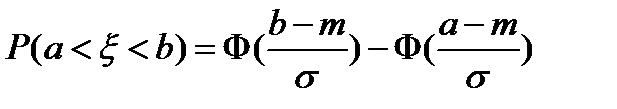. Математическое ожидание этой случайной величины равно 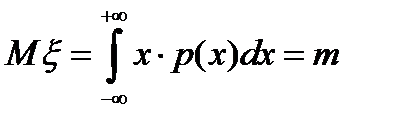. Дисперсия той же величины равна .

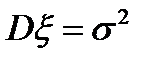Замечательным свойством нормального закона является следующее: если независимые случайные величины распределены по нормальному закону, то их сумма также распределена по нормальному закону.

Задания

1. Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины 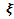соответственно равны 10 и 2 найти вероятность того, что в результате испытания 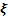примет значение, заключенное в интервале (12; 14).

2.Математическое ожидание и среднее квадратическое отклонение порога восприятия звукового сигнала в серии опытов 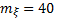(в условных единицах), дисперсия 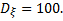Вычислить вероятность того, что в данном испытании порог будет заключен в интервале (30; 80), считая распределение порога нормальным.

3. Пусть случайная величина 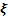«центрированная», т.е. 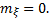Известно, что 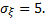Найти вероятность того, что 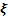не превосходитпо абсолютной величине значения 5.

4. Математическоеожидание 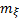и среднее квадратическое отклонение 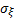уровня уверенности 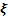, распределенного по нормальному закону, соответственно равны 40 и 0,4. Какие значения данного показателя можно гарантировать с вероятностью 0,8.

Закон больших чисел.

Вероятностные закономерности выявляются при большом числе опытов и называются законом больших чисел.Наличие этих закономерностей связано с массовостью явлений, то есть с большим числом опытов или с большим числом случайных воздействий, приводящих к такой случайной величине, которая подчиняется вполне определенному и математически выверенному закону.

Так, справедлива следующая теорема, называемая теоремой Чебышева. Если случайные величины 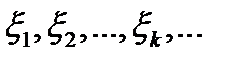попарно независимы и существует такая константа 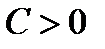, что 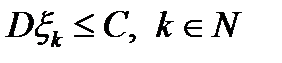, то при любом .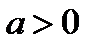

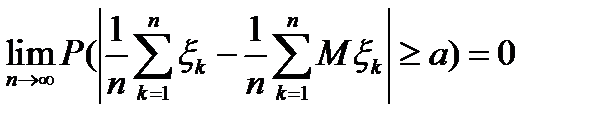То есть, какие бы конкретные значения ни принимали попарно независимые случайные величины, с большой вероятностью за их среднее можно брать среднее их математических ожиданий.

Другим примером проявления закона больших чисел является центральная предельная теорема: если последовательность попарно независимых случайных величин 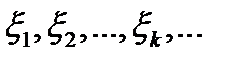удовлетворяет условию 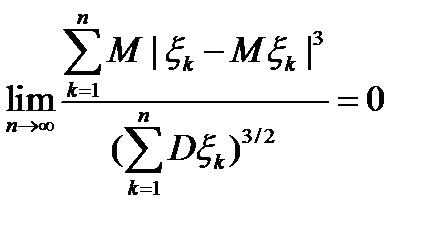, то

.

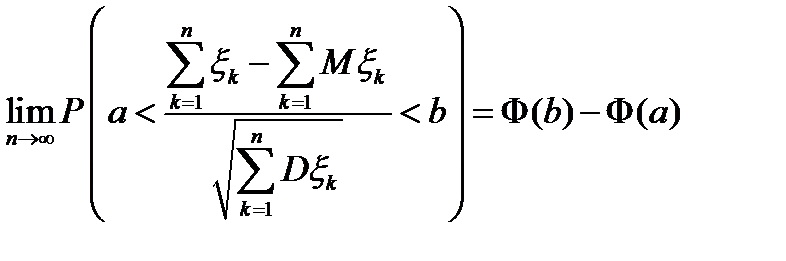Заметим, что условие, приведенное в формулировке теоремы означает, что в сумме случайных величин ни одно из слагаемых не доминирует, то есть вклад каждой из случайных величин не подавляет вкладов других величин.