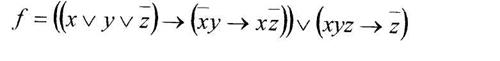Вычислительная сложность алгоритмических проблем.

Эффективность алгоритмов исследуется по отношению к трудоемкости решаемых с их помощью задач.

Вычислительной сложностью (или трудоемкостью) задачи, называется характеристика выражающая быстродействие ее решения в форме зависимости количества шагов, затрачиваемых алгоритмом на решение задачи, от размерности этой задачи.

Размерность задачи обычно представляют такие ее характеристики как количество данных, длины слова данных и т.д).

Если рассматривать алгоритм в виде МТ, то за шаг алгоритма можно принять переход от конфигурации к конфигурации, а трудоемкость задачи оценивать как зависимость от размерности задачи количества переходов от начальной конфигурации 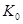к конечной конфигурации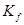

Пример 10. Анализ проверочной последовательности конфигураций из примера 9., позволяет выделить следующие стадии решения задачи копирования

копирование каждой «1» связано

- с переводом головки в позицию копирования, на которое алгоритм затрачивает n+1 шагов (по числу символов исходного слова вместе со вспомогательным символом);

- с обратным переводом головки на позицию восстановления скопированного символа, на что алгоритм затрачивает столько же n+1 шагов;

Т.к.копируется n символов исходного слова , то общая трудоемкость копирования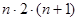

- вывод головки в исходное положение происходит за n шагов

Следовательно, общая трудоемкость решения задачи копирования числа в унарном алфавите в суммарном выражении по всем стадиям 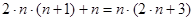,т.е. полиномиальная квадратичной сложности.

По трудоемкости все задачи принято делить на два класса: P и NP. В класс P - полиномиально разрешимых задач, входят задачи, функция трудоемкости которых задается полиномом от размерности задачи или мажорируются таким полиномом. На решение задачи иэ класса P соответствующая детерминированная МТ затрачивает полиномиальное от размерности задачи количество операций;

2} в класс неполиномиально разрешимых задач входят задачи, у которых функция трудоемкости показательная, экспонента или фак­ториал от размерности. Класс таких задач обозначается NP. На ре­шение задач из класса NP соответствующая недетерминированная МТ затрачивает полиномиальное количество операций. Заметим, что в не­детерминированной МТ параллельно, выполняемые операции во всех ко­пиях рассматриваются как одна операция, в то время как для решения той же задачи детерминированной МТ потребовалось бы количество операций, равное сумме операций во всех копиях. Так как решение за­дач из класса NP на практике связано с перебором допустимых ре­шений, то такие задачи называются переборными.

Так как любую задачу из класса P можно решить также путем полного перебора допустимых решений, то для названных классов за­дач справедливо P 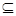NP. Вместе с тем основным вопросом теории алгоритмов яв­ляется вопрос P 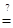NP или P 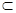NP, т.е. имеются такие переборные задачи для решения которых не возможно придумать полиномиальный по трудомкости алгоритм . В пользу последнего утверждения говорит то, что среди переборных проблем содержится достаточно большое количество известных задач, ни для одной из которых полиномиальный по трудоемкости алгоритм не найден.

Список рекомендуемой литературы

Кузнецов О.П., Адельсон – Вельский Г.М. Дискретная математика для инженера.- М. Энергоатомиздат, 1988

Горбатов В.А. Основы дискретной математики. Учебное пособие для студентов вузов.-М.Высшая школа, 1986

Мендельсон Э. Введение в математическую логику. Пер. с англ.-М.наука 1976

Гудман С., Хидетниеми С. Введение в разработку и анализ алгоритмов. М. Мир,1981

Машины Тьюринга и рекурсивные функции /Под общ. ред. Г.Д.Эбинхауза: Пер с нем. – М.Мир 1972

1) Выбрать Вариант Контрольной работы (в конце методички) по числу из двух последних цифр Зачетки (или Студенческого билета).

Если Две последние цифры Вашей зачетки от 01 до 25 то

Ваш № Вариант = Две последние цифры зачетки

Иначе Если Две последние цифры Вашей зачетки от 26 до 49 то

Ваш № Вариант = 50 -Две последние цифры зачетки

Иначе Если Две последние цифры Вашей зачетки от 50 до 74 то

Ваш № Вариант = 75 -Две последние цифры зачетки

Иначе Если Две последние цифры Вашей зачетки от 75 до 99 то

Ваш № Вариант = 100 -Две последние цифры зачетки

Иначе Ваш № Вариант =13

2) Выполнить задания Контрольной работы

МАКЕТ представления Контрольной работы.

Группа№ _________ СтудентФамилия И.О. № зачетки_______ №Варианта_______

2.1) Тест – аттестация ранее полученных знаний.

Построить таблицу истинности двоичной функции из пункта б Варианта.

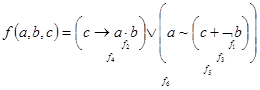
р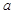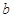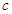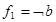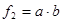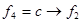

2.2) Для результирующей функции, полученной на этапе Тест – аттестации, выполнить построения, указанные в пункте б) Варианта :СДНФ, СКНФ, ПЖ, определение существенности, построение в базисах .

Например ПЖ.

Общий вид полинома от 3-х переменных

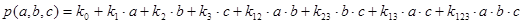
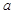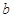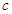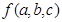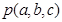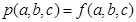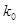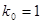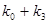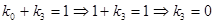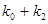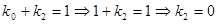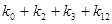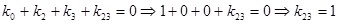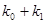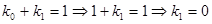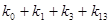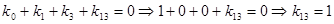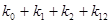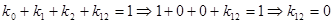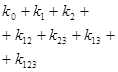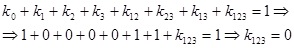Таким образом ПЖ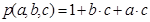

2.3) минимизировать с помощью карт Карно (Вейча) двоичную функцию от 4-х переменных, заданную аналитически, либо своими значениями на наборах

Для функций заданных аналитически ( в виде произвольных ДНФ, КНФ) по желанию минимизацию можно выполнить либо методом Блейка, либо на картах (предварительно получив значения на наборах).

Например, для функции, заданной своими значениями на наборах

а

F(a)

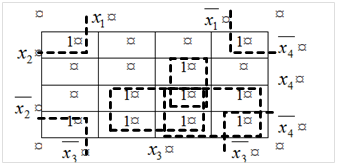
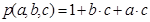
Контрольная работа

Bариант l

а) минимизировать с помощью карт Карно двоичную функцию от 4-х переменных, заданную своими значениями на наборах

a

F(a)

б) построить полином Жегалкина от функции

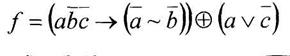
Bариант 2

а) минимизировать с помощью карт Карно двоичную функцию от 4-х переменных, заданную своими значениями на наборах

a

F(a)

б) построить полином Жегалкина от функции

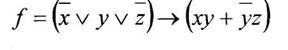
Bариант 3

а) минимизировать двоичную функцию по методу Блейка

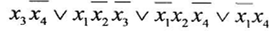
б) построить полином Жегалкина

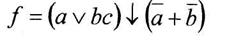
Bариант 4

а) минимизировать с помощью карт Карно двоичную функцию от 4-х переменных, заданную своими значениями на наборах

a

F(a)

б) найти существенные переменные

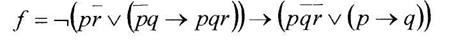
Вариант 5

а) минимизировать с помощью карт Карно двоичную функцию от 4-х переменных, заданную своими значениями на наборах

а

F(a)

б) построить полином Жегалкина от функции

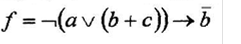
Вариант 6

а) минимизировать с помощью карт Карно двоичную функцию от 4-х переменных, заданную своими значениями на наборах

а

F(a)

б) построить СДНФ функции

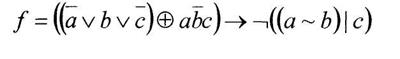
Вариант 7

а) минимизировать двоичную функцию по методу Блейка

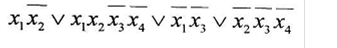
б) построить СДНФ функции

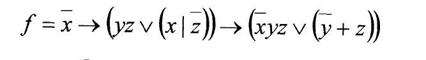
Вариант 8

а) минимизировать двоичную функцию по методу Блейка

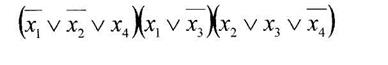
б) построить полином Жегалкина

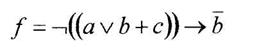
Вариант 9

а) минимизировать с помощью карт Карно двоичную функцию от 4-х переменных, заданную своими значениями на наборах

а

F(a)

б) построить СДНФ функции

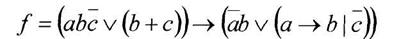
Вариант 10

а) минимизировать с помощью карт Карно двоичную функцию от 4-х переменных, заданную своими значениями на наборах

а

F(a)

б) построить СДНФ функции

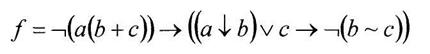
Вариант 11

а) минимизировать двоичную функцию по методу Блейка

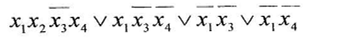
б) построить СКНФ функции

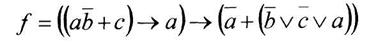
Вариант 12

а) минимизировать двоичную функцию по методу Блейка

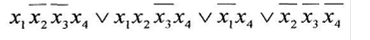
б) построить СКНФ функции

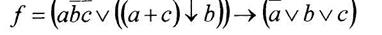
Вариант 13

а) минимизировать с помощью карт Карно двоичную функцию от 4-х переменных, заданную своими значениями на наборах

а

F(a)

б) построить СКНФ функции

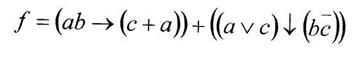
Вариант 14

а) минимизировать с помощью карт Карно двоичную функцию от 4-х переменных, заданную своими значениями на наборах

а

F(a)

б) построить СКНФ функции

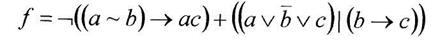
Вариант 15

а) минимизировать с помощью карт Карно двоичную функцию от 4-х переменных, заданную своими значениями на наборах

а

F(a)

б) построить СКНФ функции

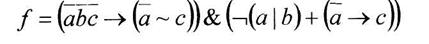
Вариант 16

а) минимизировать с помощью карт Карно двоичную функцию от 4-х переменных, заданную своими значениями на наборах

а

F(a)

б) построить формулу с помощью различных базисов А-Ж

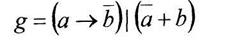
Вариант 17

а) минимизировать двоичную функцию по методу Блейка

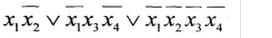
5) построить формулу с помощью

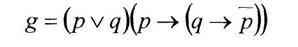
Вариант 18

а) минимизировать двоичную функцию по методу Блейка

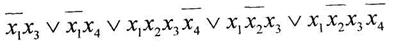
б) построить формулу с помощью различных базисов А-Ж

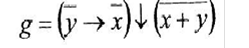
Вариант 19

а) минимизировать двоичную функцию по методу Блейка

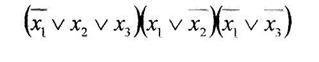
б) построить формулу с помощью различных базисов А-Ж

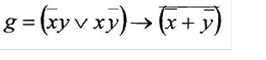
Вариант 20

а) минимизировать двоичную функцию по методу Блейка

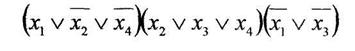
б) построить формулу с помощью различных базисов А-Ж

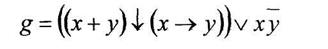
Вариант 21

а) минимизировать двоичную функцию по методу Блейка

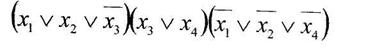
б) найти существенные переменные функции

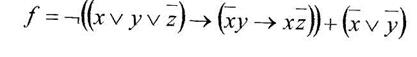
Вариант 22

а) минимизировать двоичную функцию по методу Блейка

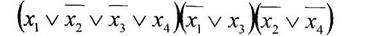
б) найти существенные переменные функции

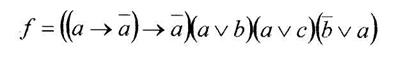
Вариант 23

а) минимизировать двоичную функцию по методу Блейка

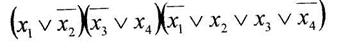
б) найти существенные переменные функции

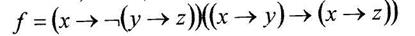
Вариант 24

а) минимизировать двоичную функцию по методу Блейка

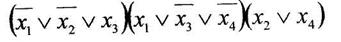
б) найти существенные переменные функции

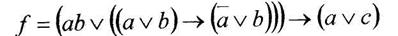
Вариант 25

а) минимизировать двоичную функцию по методу Блейка

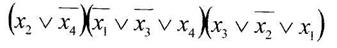
б) найти существенные переменные функции