Распределенность терминов в простых категорических суждениях.

Распределенность терминов.

Термин считает распределённым, т.е. развёрнутым, исчерпанным, взятом в полном объёме, если в суждении речь идёт обо всех объектах входящих в объем этого термина.
Обозначается знаком «+».
Термин считается нераспределённым, т.е. неразвёрнутым, неисчерпанным, взятом в неполном объёме, если в суждении речь идёт не обо всех объектах, входящих в объём этого термина. Обозначается знаком « – »
Н: все акулы являются хищниками. S – акулы, все – кванта,P – хищники.

Реляционные суждения.

Обозначается «R (x, y, z…)». R – выражает отношение между предметами (x, y, z…). В зависимости от количества предметов связанных отношением R, предикат, выражающий эти отношения, называется двухместным, трёхместным, n-местным.

Двухместное (xRy) где x – предшествующий член, y – последующий член отношения R.

а) прямое и обратное отношение. Отношения, зафиксированные в некотором реляционном суждении можно изменить таким образом, что предшествующий член станет последующим, и наоборот.
Н: 2 меньше 3 изменяем и получаем 3 меньше 2.
Конверсия (изменение) реляционного суждения основана на подборе некоего отношения R1 обратного отношению R. Суждения, основанные на взаимной конверсии отношении синонимичны и,следовательно, взаимозаменяемы.

б) симметричные, ассиметричные, несимметричные отношения. Есть реляционные суждения для конверсии, которых достаточно поменять местами x и y, оставляя R неизменным.

Н: Иван родственник Петра, Петр родственник Ивана.

Если на отношение R не влияет, какой из членов x или y является предшествующим а, какой последующим то такое отношение называется симметричным (предикаты – родственник, современник, ровесник). Существуют отношения, которые, связывая произвольные x и y в истинных реляционных суждениях при перестановке предшествующего и последующего членов, с необходимостью дают ложные суждения. Такие отношения называются ассиметричными (P – отец, муж, больше, предок и т.д.). Имеются отношения, которые не являются не симметричными не ассиметричными. Такие отношения называются несимметричными.

Н: Иван любит Марью. P: любить, уважать, завидовать и т.п.

в) транзитивные и не транзитивные отношения. Если отношение R связывает попарно предметы x, y и y, z; с необходимостью связывает также x,z; то это отношение называется транзитивным. Зная, что данное отношения транзитивно мы можем из структур xRy и yRz вывести структуру xRz.

Н: ул. Садовая параллельная ул. Логинова, соответственно ул. Логинова параллельна ул. Попова, соответственно ул. Садовая параллельна ул. Попова.

P транзитивных отношении: быть равным. предок, больше и. т.д.
Отношение, не обладающее свойством транзитивности, называется не транзитивным.
Pне транзитивных отношении: отец, знакомый, пересекать и. т.д.

14.Отношения между суждениями по “логическому квадрату”.

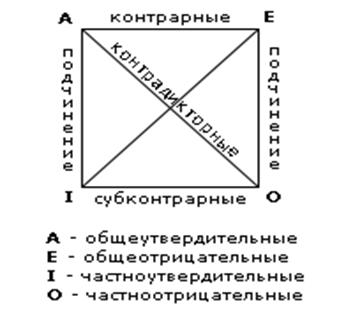Диаграмма, служащая для мнемонического запоминания логических отношений между видами суждений по объединенной классификации. Вершины квадрата обозначают вид суждения по объединенной классификации А , Е , 0 , I. Стороны и диагонали символизируют логические отношения между простыми суждениями (кроме эквивалентных). Верхняя сторона есть О отношение А и Е - противоположность (контрарность); нижняя сторона - отношение между I и O - частичная совместимость(субконтрарность);две вертикальные стороны - отношения между А и I (левая), Е и О (правая) - подчинение; диагонали - отношения между А и О, Е и I- противоречие(контрадикторность).

Отношения противоположности – суждения находящиеся в отношении противоположности не могут быть одновременно истинными, но могут быть одновременно ложными.

Все мужчины галантны. Ни один мужчина не галантен. Если одно из противоположных истинно, то другое ложно, но не наоборот. А истинно, Е ложно. ∀ (x)(S(x) ⊃ P(x)) ⊃ ∀- (x)(S(x) ⊃ P-(x)) Если верно, что все S суть P, то неверно, что ни одно S не суть P.

Отношения противоречия – суждения находящиеся в состоянии противоречия не могут быть одновременно не ложными, не истинными. Если одно из них истинно, то другое непременно ложно, и наоборот. А истинно, O – ложно. ∀ (x)(S(x) ⊃ P(x)) ⊃ ∃- (x)(S(x) ⋀ P-(x)) Если верно, что все S суть P, то неверно, что некоторые S не суть P.

Отношения подчинения – суть отношений подчинения заключается в том, что истинность подчинённых суждений, гарантируется истинностью общих суждений. Ложность подчинённых, обуславливает ложность общих. A истинно, E – ложно. ∀ (x)(S(x) ⊃ P(x)) ⊃ ∃ (x)(S(x) ⋀ P(x)) Если верно, что все S суть P, то верно, что и некоторые S суть P. Отношения подпротивности – суждения находящиеся в отношении подпротивности не могут быть одновременно ложными, но могут быть одновременно истинными. Если одно из суждений ложно, то другое непременно истинно, но не наоборот.