Графы, деревья, фреймы и сети, нейронные сети, генетические алгоритмы

Моделирование

Модель и моделирование – это универсальные понятия, атрибуты одного из наиболее мощных методов познания в любой профессиональной области, познания объекта, процесса, явления (через модели и моделирование).

Модели и моделирование объединяют специалистов различных областей, работающих над решением межпредметных проблем, независимо от того, где эта модель и результаты моделирования будут применены.

Модель – это некоторое представление или описание оригинала (объекта, процесса, явления), которое при определенных предложениях, гипотезах о поведении оригинала позволяет замещать оригинал для его лучшего изучения, исследования, описания его свойств.

Существует два основных способа моделирования:

1. Физическое моделирование. Создается физическая копия объекта, на которой изучаются свойства/поведение объекта (проводятся испытания). Эта копия может копировать как объект целиком, так и только некоторые структуры объекта, требующие изучения. Также при физическом моделировании часто используются уменьшенные копии объекта (например макеты зданий/объектов, испытание моделей самолетов в аэродинамической трубе и т.п. ).

2. Информационное моделирование.

В зависимости от вида данных и способов их обработки (алгоритмов обработки) используются следующие информационные модели.

Моделирование - процесс изучение объекта (его свойств, поведения) на его модели.

Пример. Рассматривая физическое тело, брошенное с высоты h и падающее свободно в течение t времени, можно записать соотношение: h = gt²/2 . Это физико-математическая модель системы (математическая модель физической системы) пути при свободном падении тела. При построении этой модели приняты следующие гипотезы: 1) падение происходит в вакууме (то есть коэффициент сопротивления воздуха равен нулю); 2) ветра нет; 3) масса тела неизменна; 4) тело движется с одинаковым постоянным ускорением g в любой точке.

Проблема моделирования состоит из трех взаимосвязанных задач: построение новой (адаптация известной) модели; исследование модели (разработка метода исследования или адаптация, применение известного); использование (на практике или теоретически) модели.

Схема построения модели М системы S с входными сигналами X и выходными сигналами Y изображена на рисунке.

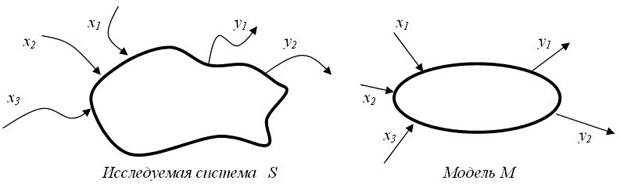
Рисунок – Схема построения модели

Если на вход М поступают сигналы X и на входе появляются сигналы Y, то задан закон, правило f функционирования модели, системы.

Классификацию моделей проводят по различным критериям.

Модель – статическая, если среди параметров описания модели нет (явно) временного параметра.

Модель – динамическая, если среди параметров модели явно выделен временной параметр.

Модель – дискретная, если описывает поведение оригинала лишь дискретно, например в дискретные моменты времени (для динамической модели).

Модель – непрерывная, если описывает поведение оригинала на всем промежутке времени.

Модель – детерминированная, если для каждой допустимой совокупности входных параметров она позволяет определять однозначно набор выходных параметров; в противном случае – модель недетерминированная, стохастическая (вероятностная).

Модель – функциональная, если представима системой функциональных соотношений (например, уравнений).

Модель – теоретико-множественная, если представима некоторыми множествами и отношениями их и их элементов.

Модель – логическая, если представима предикатами, логическими функциями и отношениями.

Модель – информационно-логическая, если она представима информацией о составных элементах, подмоделях, а также логическими отношениями между ними.

Модель – игровая, если она описывает, реализует некоторую игровую ситуацию между элементами (объектами и субъектами игры).

Модель – алгоритмическая, если она описана некоторым алгоритмом или комплексом алгоритмов, определяющим ее функционирование, развитие.

Модель – графовая (сетевая), если она представима графом (отношениями вершин и соединяющих их ребер) или графами и отношениями между ними.

Модель – иерархическая (древовидная), если она представима иерахической структурой (деревом).

Модель – языковая, лингвистическая, если она представлена некоторым лингвистическим объектом, формализованной языковой системой или структурой. Иногда такие модели называют вербальными, синтаксическими и т.п.

Модель – визуальная, если она позволяет визуализировать отношения и связи моделируемой системы, особенно в динамике.

Модель – натурная, если она есть материальная копия оригинала.

Модель – геометрическая, если она представима геометрическими образами и отношениями между ними.

Модель – имитационная, если она построена для испытания или изучения, проигрывания возможных путей развития и поведения объекта путем варьирования некоторых или всех параметров модели.

Модель – алгоритмическая (математическая) – моделирование реализуется с помощью различных алгоритмов. Такое моделирование используется для объектов поведение/свойства, которых можно описать математически (изменение свойств, которых происходит по известным математическим/физическим закономерностям). Примеры: алгоритмы решения степенных уравнений, алгоритмы построения кривых в векторной графике, алгоритмы построения многогранных (объемных) объектов и моделирования отражения света в 3D графике, алгоритмы расчета тока/напряжения/сопротивления в сети и т.п.

Модель – статистическая – данные обрабатываются статистическими методами, такой вид моделирования используются для трудно формализуемых задач (сюда относятся «чисто статистические» методы и методы на основе распознавания образов).

М – реляционная (табличная) – данные модели организуются в виде двумерных таблиц, строки которых соответствуют записям, а столбцы – полям. Для обработки таких моделей используется алгебра отношений (реляционное исчисление).

Модель – конечного автомата – описывает систему как абстрактную математическую машину. В этой модели переменные состояния представляют состояния машины, а функции перехода описывают способ изменения переменных.

Модель – черный ящик – если известны величины входов и выходов, а внутреннее содержание модели неизвестно.

Есть и другие типы моделей.

Правила правописания – языковая, структурная модель. Глобус – натурная географическая модель земного шара. Макет дома является натурной геометрической моделью строящегося дома. Вписанный в окружность многоугольник дает визуальную геометрическую модель окружности на экране компьютера.

Тип модели зависит от связей и отношений его подсистем и элементов, окружения, а не от его физической природы.

Пример. Математические описания (модели) динамики эпидемии инфекционной болезни, радиоактивного распада, усвоения второго иностранного языка, выпуска изделий производственного предприятия и т.д. являются одинаковыми с точки зрения их описания, хотя процессы различны.

Основные свойства любой модели:

· целенаправленность;

· конечность;

· упрощенность;

· приблизительность;

· адекватность;

· информативность;

· полнота;

· замкнутость и др.

Жизненный цикл моделируемой системы:

· сбор информации;

· проектирование;

· построение;

· исследование;

· оценка;

· модификация.

Наука моделирования состоит в разделении процесса моделирования (системы, модели) на этапы (подсистемы, подмодели), детальном изучении каждого этапа, взаимоотношений, связей, отношений между ними и затем эффективного описания их с максимально возможной степенью формализации и адекватности.

Примеры применения математического, компьютерного моделирования в различных областях:

энергетика: управление ядерными реакторами, моделирование термоядерных процессов, прогнозирование энергетических процессов, управление энергоресурсами и т.д.;

экономика: моделирование, прогнозирование экономических и социально-экономических процессов, межбанковские расчеты, автоматизация работ и т.д.;

космонавтика: расчет траекторий и управления полетом космических аппаратов, моделирование конструкций летательных аппаратов, обработка спутниковой информации и т.д.;

медицина: моделирование, прогнозирование эпидемий, инфекционных процессов, управление процессом лечения, диагностика болезней и выработка оптимальных стратегий лечения и т.д.;

производство: управление техническими и технологическими процессами и системами, ресурсами (запасами), планирование, прогнозирование оптимальных процессов производства и т.д.;

экология: моделирование загрязнения экологических систем, прогноз причинно-следственных связей в экологической системе, откликов системы на те или иные воздействия экологических факторов и т.д.;

образование: моделирование междисциплинарных связей и систем, стратегий и тактик обучения и т.д.;

военное дело: моделирование и прогнозирование военных конфликтов, боевых ситуаций, управления войсками, обеспечение армий и т.д.;

политика: моделирование и прогнозирование политических ситуаций, поведения коалиций различного характера и т.д.;

социология, общественные науки: моделирование и прогнозирование поведения социологических групп и процессов, общественного поведения и влияния, принятие решений и т.д.;

СМИ: моделирование и прогнозирование эффекта от воздействия тех или иных сообщений на группы людей, социальные слои и др.;

туризм: моделирование и прогнозирование потока туристов, развития инфраструктуры туризма и др.;

проектирование: моделирование, проектирование различных систем, разработка оптимальных проектов, автоматизация управления процессом проектирования и т.д.

Современное моделирование сложных процессов и явлений невозможно без компьютера, без компьютерного моделирования.

Компьютерное моделирование – основа представления (актуализации) знаний как в компьютере, так и с помощью компьютера и с использованием любой информации, которую можно актуализировать с помощью ЭВМ.

Разновидность компьютерного моделирования – вычислительный эксперимент, осуществляемый экспериментатором над исследуемой системой или процессом с помощью орудия эксперимента – компьютера, компьютерной технологии. Вычислительный эксперимент позволяет находить новые закономерности, проверять гипотезы, визуализировать события и т.д.

Компьютерное моделирование от начала и до завершения проходит следующие этапы:

· постановка задачи;

· предмодельный анализ;

· анализ задачи;

· исследование модели;

· программирование, проектирование программы;

· тестирование и отладка;

· оценка моделирования;

· документирование;

· сопровождение;

· использование (применение) модели.

Графы, деревья, фреймы и сети, нейронные сети, генетические алгоритмы

Фрейм - структуру данных для представления стереотипных ситуаций. Фрейм - средство, которое помогло связать декларативные и процедурные знания о некоторой сущности в структуру записей, которая состоит из слотов и наполнителей (filler). Слоты играют ту же роль, что и поля в записи, а наполнители – это значения, хранящиеся в полях.

Эта структура наполнена самой разнообразной информацией: об объектах и событиях, которые следует ожидать в этой" ситуации, и о том, как использовать информацию, имеющуюся во фрейме. Идея состоит в том, чтобы сконцентрировать все знания о данном классе объектов или событий в единой структуре данных, а не распределять их между множеством более мелких структур вроде логических формул или порождающих правил.

Графы. Для описания многих видов абстрактных данных в информатике вообще и в теории искусственного интеллекта, в частности, очень широко используется терминология, заимствованная из теории графов.

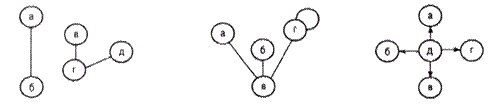
Все определения сформулированы в предположении, что существуют два вида примитивов - узлы и связи. Узлы представляют собой исходящие и целевые пункты для связей

и обычно каким-либо образом промаркированы. Связи также могут быть промаркированы,

Рисунок – Некоторые виды графов: а) обыкновенный граф; б) связный граф с петлей; в) обыкновенный ориентированный граф – дерево

но это не обязательно. Все зависит от того, имеем ли мы дело со связями одного вида или разных. В общепринятой терминологии теории графов узлы называются "вершинами", а связи - "ребрами графа", или "дугами".

Если N- множество узлов, то любое подмножество NxN является обобщенным графом G. Если в парах подмножества NxN имеет значение порядок, то граф G является ориентированным.

Граф не обязательно должен быть связным. Если задаться условием, что петли не допускаются, т.е. в каждой паре должны присутствовать разные узлы, то такой граф называется обыкновенным. Если на графе не допускаются не только петли, но и циклы (т.е. последовательность связей, в которой начальный и конечный узлы совпадают), то такой граф называется лесом.

Если G- обыкновенный граф, в котором имеется n узлов и n-1 связей и отсутствуют циклы, то такой граф является деревом.

Иными словами, дерево - это связный лес. Обычно один из узлов дерева является его корнем. Остальные узлы образуют ветвящуюся структуру "наследников" корневого узла, в которой отсутствуют циклы. Узлы, не имеющие наследников, являются терминальными, или "листьями" дерева, а остальные узлы называются промежуточными (нетерминальными).

Сети. В теории графов сетью называется взвешенный ориентированный граф, т.е. граф, в котором каждой связи сопоставлено определенное число. Обычно этими числами оценивается "стоимость" пути вдоль этой связи или длина связи, как на карте дорог. В каждом конкретном случае применения графа как формального средства описания проблемы эти числа могут трактоваться по-своему.

Связи в сети практически всегда являются ориентированными, поскольку отношения, представленные взвешенными связями, не должны быть симметричными.

Обыкновенные графы используются для представления взаимоотношений между объектами в пространстве или во времени. Доступ к такой информации связан в той или иной мере с использованием специальных средств прослеживания путей на графе, для которых разработаны самые различные алгоритмы.

Для представления иерархических классификаций и сетей применяются деревья. Например, на рисунке показано дерево классификации болезней по расположению пораженного органа. Корневой узел дерева представляет множество всех болезней, а его наследники - группы болезней, соответствующие основному пораженному органу. Каждый из этих узлов

будет иметь своих наследников, представляющих более узкие группы болезней, и т.д. Терминальные узлы дерева будут представлять конкретные заболевания.

Семантические сети вначале использовались для представления смысла выражений естественного языка человека, откуда и появилось название этого класса сетей. Теперь же

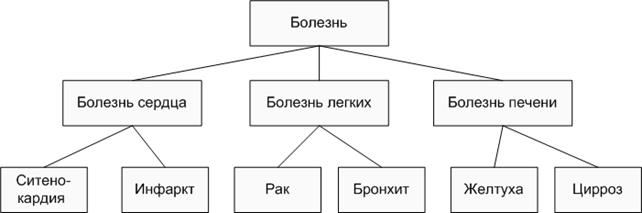
Рисунок – Обыкновенное дерево классификации болезней

они используются в качестве структуры, пригодной для представления информации общего вида, - узлы представляют некоторые концепты (понятия), а связи - отношения между концептами.

Нейронные сети.В самом упрощенном виде нейронную сеть можно рассматривать как способ моделирования в технических системах принципов организации и механизмов функционирования головного мозга человека.

Согласно современным представлениям, кора головного мозга человека представляет собой множество взаимосвязанных простейших ячеек - нейронов, количество которых оценивается числом порядка 10¹⁰. Технические системы, в которых предпринимается попытка воспроизвести, пусть и в ограниченных масштабах, подобную структуру (аппаратно или программно), получили наименование нейронные сети.

Нейрон головного мозга получает входные сигналы от множества других нейронов, причем сигналы имеют вид электрических импульсов. Входы нейрона делятся на две категории - возбуждающие и тормозящие. Сигнал, поступивший на возбуждающий вход, повышает возбудимость нейрона, которая при достижении определенного порога приводит к формированию импульса на выходе. Сигнал, поступающий на тормозящий вход, наоборот, снижает возбудимость нейрона. Каждый нейрон характеризуется внутренним состоянием и порогом возбудимости. Если сумма сигналов на возбуждающих и тормозящих входах нейрона превышает этот порог, нейрон формирует выходной сигнал, который поступает на входы связанных с ним других нейронов, т.е. происходит распространение возбуждения по нейронной сети.

Было обнаружено, что время переключения отдельного нейрона головного мозга составляет порядка нескольких миллисекунд, т.е. процесс переключения идет достаточно медленно. Поэтому исследователи пришли к заключению, что высокую производительность обработки информации в мозге человека можно объяснить только параллельной работой множества относительно медленных нейронов и большим количеством взаимных связей между ними. Именно этим объясняется широкое распространение термина "массовый параллелизм" в литературе, касающейся нейронных сетей.

Генетические алгоритмы (ГА) представляют собой новое направление в алгоритмике. Они способны не только решать и сокращать перебор в сложных задачах, но и легко адаптироваться к изменению проблемы.

Генетический алгоритм - это алгоритм поиска оптимального решения, который случайным образом выбирает начальную популяцию таких решений и затем подвергает их процессу искусственных мутаций, скрещивания и отбора по аналогии с естественным отбором

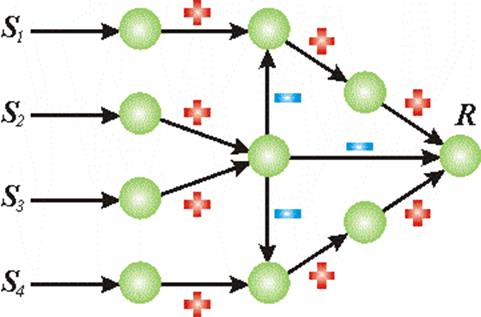Рисунок – Фрагмент нейронной сети с возбуждающими и тормозящими связями

Вначале ГА-функция генерирует определенное количество возможных решений, а затем вычисляет для каждого «уровень выживаемости» (fitness) - близость к истине. Эти решения дают потомство. Те что «сильнее», то есть больше подходят, имеет больший шанс к воспроизводству, а «слабые» постепенно отмирают. Идет эволюция.

Процесс повторяется до тех пор, пока не найдено решение, или не получено достаточное к нему приближение. Правильно запрограммированные генетические алгоритмы могут быть просто суперэффективны.

Схема генетического алгоритма.

1.Генерация случайного начального состояния. Первое поколение создается из произвольно выбранных решений (хромосом). Это отличается от стандартных методов, когда начальное состояние всегда одно и то же.

2.Вычисление коэффициента выживаемости (fitness). Каждому решению (хромосоме) сопоставляется некое численное значение, зависящее от его близости к ответу.

3.Воспроизводство. Хромосомы, имеющие большую выживаемость (fitness), попадают к потомкам (которые затем могут мутировать) с большей вероятностью. Потомок, результат слияния «отца» и «матери», является комбинаций их ген. Этот процесс называется «кроссинговер» (crossing over).

4.Следующее поколение. Если новое поколение содержит решение, достаточно близкое к ответу, то задача решена. В противоположном случае оно проходит через тот же процесс. Это продолжается до достижения решения.

Экспертные системы

Экспертная система - это программа для компьютера, которая оперирует со знаниями в определенной предметной области с целью выработки рекомендаций или решения проблем.

Экспертная система может полностью взять на себя функции, выполнение которых обычно требует привлечения опыта человека-специалиста, или играть роль ассистента для человека, принимающего решение. Другими словами, система (техническая или социальная), требующая принятия решения, может получить его непосредственно от программы или через промежуточное звено - человека, который общается с программой. Тот, кто принимает решение, может быть экспертом со своими собственными правами, и в этом случае программа может "оправдать" свое существование, повышая эффективность его работы. Альтернативный вариант - человек, работающий в сотрудничестве с такой программой, может добиться с ее помощью результатов более высокого качества. Вообще говоря, правильное распределение функций между человеком и машиной является одним из ключевых условий высокой эффективности внедрения экспертных систем.

Технология экспертных систем является одним из направлений новой области исследования, которая получила наименование искусственного интеллекта (Artificial Intelligence - AI). Исследования в этой области сконцентрированы на разработке и внедрении компьютерных программ, способных эмулировать (имитировать, воспроизводить) те области деятельности человека, которые требуют мышления, определенного мастерства и накопленного опыта. К ним относятся задачи принятия решений, распознавания образов и понимания человеческого языка. Эта технология уже успешно применяется в некоторых областях техники и жизни общества - органической химии, поиске полезных ископаемых, медицинской диагностике. Перечень типовых задач, решаемых экспертными системами, включает:

· извлечение информации из первичных данных (таких как сигналы, поступающие от гидролокатора);

· диагностика неисправностей (как в технических системах, так и в человеческом организме);

· структурный анализ сложных объектов (например, химических соединений);

· выбор конфигурации сложных многокомпонентных систем (например, распределенных компьютерных систем);

· планирование последовательности выполнения операций, приводящих к заданной цели (например, выполняемых промышленными роботами).

Экспертная система отличается от прочих прикладных программ наличием следующих признаков.

· Моделирует не столько физическую (или иную) природу определенной проблемной области, сколько механизм мышления человека применительно к решению задач в этой проблемной области. Это существенно отличает экспертные системы от систем математического моделирования или компьютерной анимации. Нельзя, конечно, сказать, что программа полностью воспроизводит психологическую модель специалиста в этой предметной области (эксперта), но важно, что основное внимание все-таки уделяется воспроизведению компьютерными средствами методики решения проблем, которая применяется экспертом, -т.е. выполнению некоторой части задач так же (или даже лучше), как это делает эксперт.

· Система, помимо выполнения вычислительных операций, формирует определенные соображения и выводы, основываясь на тех знаниях, которыми она располагает. Знания в системе представлены, как правило, на некотором специальном языке и хранятся отдельно от собственно программного кода, который и формирует выводы и соображения. Этот компонент программы принято называть базой знаний.

· При решении задач основными являются эвристические и приближенные методы, которые, в отличие от алгоритмических, не всегда гарантируют успех. Эвристика, по существу, является правилом влияния (rule of thumb), которое в машинном виде представляет некоторое знание, приобретенное человеком по мере накопления практического опыта решения аналогичных проблем. Такие методы являются приблизительными в том смысле, что, во-первых, они не требуют исчерпывающей исходной информации, и, во-вторых, существует определенная степень уверенности (или неуверенности) в том, что предлагаемое решение является верным.