Признак равносильности формул 3 страница

2. ФУНКЦИИ АЛГЕБРЫ ЛОГИКИ И

ИХ ПРИЛОЖЕНИЯ

2.1. Функции алгебры логики

Функции алгебры логики называют булевыми функциями в честь английского математика Джорджа Буля (1815–1864).

Определение 1. Булевой функцией 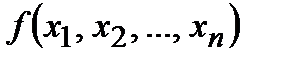от n аргументов называется функция f, заданная на множестве 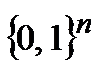и принимающая значения в двухэлементном множестве 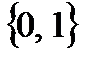. Другими словами, булева функция от n аргументов сопоставляет каждому упорядоченному набору, составленному из элементов 0 и 1, либо 0, либо 1.

Здесь 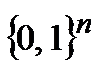– есть n-я декартова степень множества .

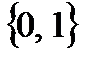Теорема 1. Число всех различных функций алгебры логики 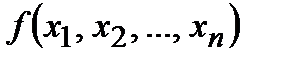от n переменных равно .

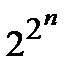Всякая функция алгебры логики 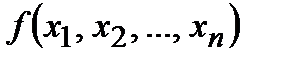может быть задана с помощью таблицы истинности.

Определение 2. Говорят, функция алгебры логики 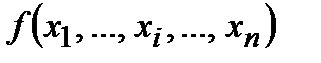несущественно зависит от переменной x_i, если для лю­бых двух наборов 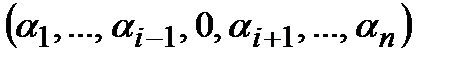, 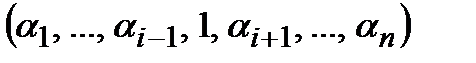из области определения 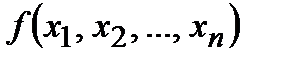имеет место

.

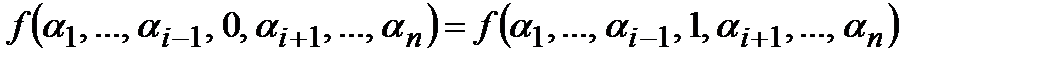Например, функция 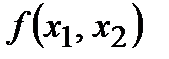от двух переменных, заданная таблицей

0 0
0 1
1 0
1 1

несущественно зависит от переменной х₁ а именно, 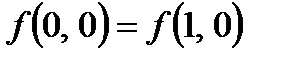и .

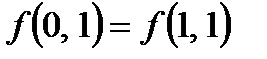Очевидно, множество всех функций алгебры логики 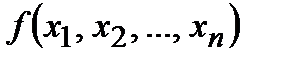от n переменных наряду с функциями, которые существен­но зависят от всех n переменных, содержат все функции, которые несущественно зависят от некоторой части своих переменных.

Среди функций алгебры логики, зависящих от одной и двух переменных, выделим функции, представленные в таблице:

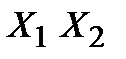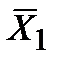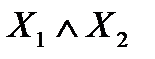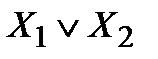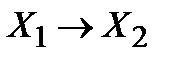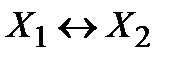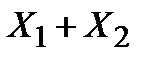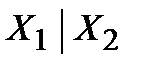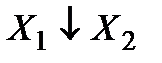0 0
0 1
1 0
1 1

Функция, представленная во втором столбце, называется отрицанием соответствующей переменной, а функции, представленные в остальных столбцах – соответственно конъюнкцией, дизъюнкцией, импликацией, эквивалентностью, суммой по модулю 2, штрихом Шеффера, стрелкой Пирса переменных .

Заимствуя соответствующие результаты из алгебры высказываний, для функций алгебры логики можно сформулировать аналогичные теоремы.

Теорема 2. Любая функция алгебры логики 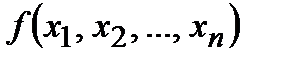, не равная тождественно нулю, имеет СДНФ:

.

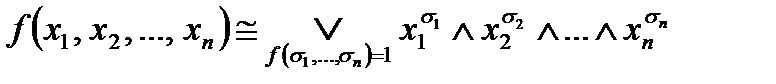Теорема 3. Любая функция алгебры логики 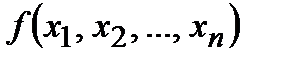, не равная тождественно единице, имеет СКНФ:

.

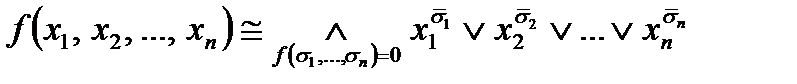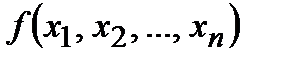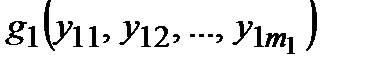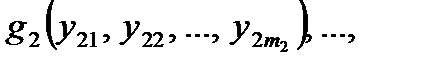
Определение 3.Если , , 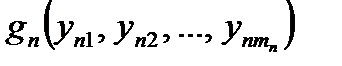– функции алгебры логики со­ответственно от 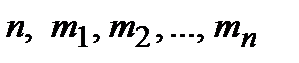переменных, то функция

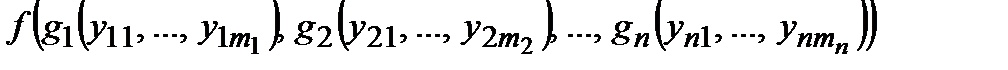
называется суперпозицией функций 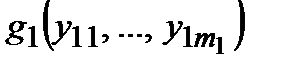, , 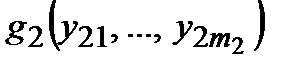…, 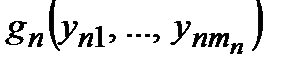в функцию .

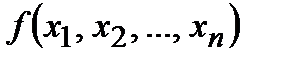Таким образом, имея в наличии некоторые функции алгебры логики, мы с помощью суперпозиций имеющихся функций можем строить новые функции.

Например, пусть заданы таблицей функции

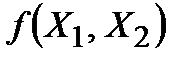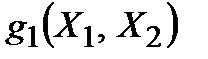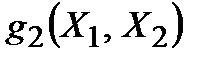0 0
0 1
1 0
1 1

Образовав их суперпозицию 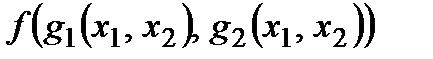, получим новую функцию от переменных 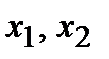, таблица которой имеет вид

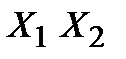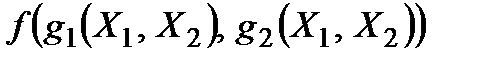0 0
0 1
1 0
1 1

Определение 4. Множество функций алгебры логики R на­зывается замкнутым, если любая суперпозиция функций из множе­ства R принадлежит множеству R.

Определение 5. Система функций алгебры логики 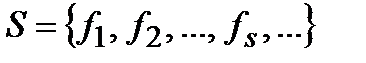называется полной, если для любой функции алгебры логики 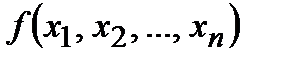найдется суперпозиция функций из S, совпадающая с .

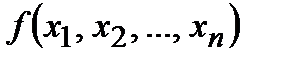Примеры.

1.Система функций алгебры логики 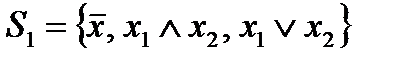является полной. Полнота указанной системы следует из того, что любая функция алгебры логики имеет либо СДНФ, либо СКНФ, а каждая СДНФ и СКНФ представляет собой суперпозицию функций из .

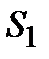2. Система функций 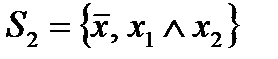является полной. Полнота этой системы следует из полноты предыдущей системы, ес­ли учесть, что .

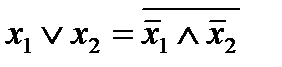Вообще справедлива следующая теорема.

Теорема 4. Пусть S и S ' – две системы функций алгебры ло­гики, о которых известно следующее: система S является полной и каждая функция из S выражается через суперпозицию функций из S '. Тогда система S ' также является полной.

Так, система 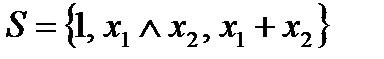является полной систе­мой, так как любая функция полной системы 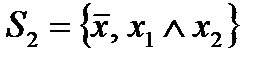выражает­ся через функции системы S. Именно,

.

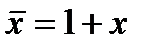Используя полноту системы S, можно показать, что любая функция алгебры логики 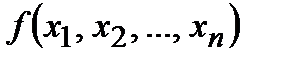имеет однозначное с точно­стью до перестановки членов представление

,

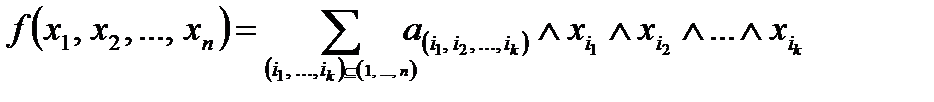где 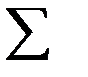– сумма по модулю 2, a .

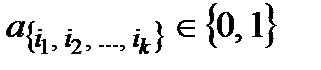Это представление функции называется полиномом Жегалкина.

В теории функций алгебры логики проблема полноты за­ключается в следующем: по заданной системе функций алгебры ло­гики нужно эффективно ответить на вопрос, является заданная сис­тема функций полной или нет.

Проблема полноты функций алгебры логики была решена Постом на языке предполных замкнутых классов функций алгебры логики.

2.2. Специальные замкнутые классы функций алгебры логики

Определение 6. Функция 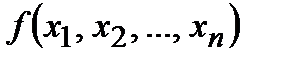алгебры логики принадлежит классу функций Т₀, сохраняющих константу 0, то­гда и только тогда, когда .

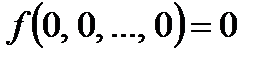Определение 7. Функция 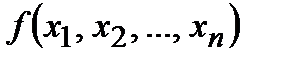алгебры логики принадлежит классу функций Т₁, сохраняющих константу 1, тогда и только тогда, когда .

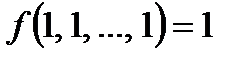Определение 8. Функция 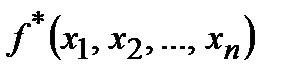называется двойст­венной к функции 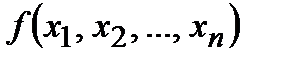, если для любого набора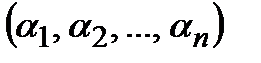

.

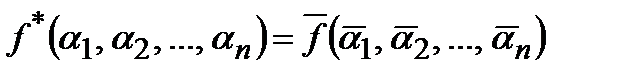Определение 9.Функция 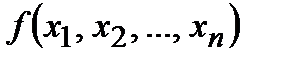называется самодвойственной, если 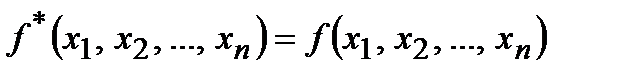. Класс всех самодвойственных функций обозначим через S.

Теорема 5(признак самодвойственности). Функция является самодвойственной тогда и только тогда, когда на любых противоположных наборах она принимает противоположные значения.

На множестве двоичных наборов введем отношение частичного порядка 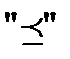по следующему принципу:

.

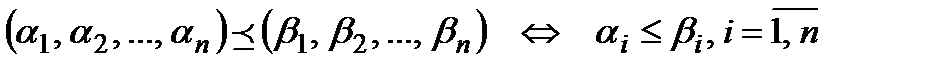Полагается, что .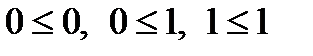

В соответствии с введенным отношением порядка дадим следующее определение монотонной функции алгебры логики.

Определение 10. Функция 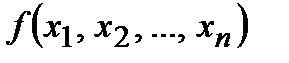алгебры логики принадлежит классу монотонных функций алгебры логики М тогда и только тогда, когда для любых двух наборов 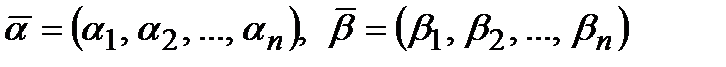таких, что 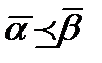, имеет место .

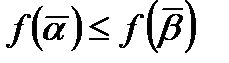Определение 11. Функция 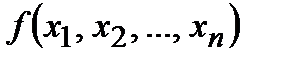алгебры логики принадлежит классу линейных функций алгебры логики L тогда и только тогда, когда

,

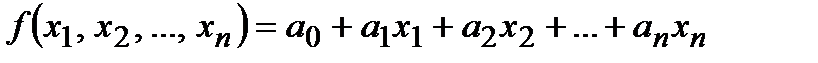где 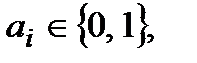а "+" есть сумма по модулю 2.

Нетрудно показать, что все перечисленные выше классы функций алгебры логики являются замкнутыми классами функций. Более того, любой замкнутый класс функций алгебры логики при­надлежит, по крайней мере, одному из перечисленных классов, то есть указанные выше классы являются максимальными замкнутыми классами функций алгебры логики.

Теперь сформулируем теорему Поста.

Теорема 6(теорема Поста).Система 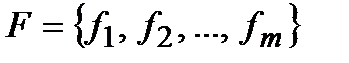булевых функций является полной тогда и только тогда, когда для каждого из классов T₀, T₁, S, M, L в системе F найдется функция, не принадлежащая этому классу.

Согласно теореме Поста для разрешения вопроса полноты относительно некоторой системы функций 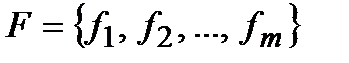дос­таточно заполнить следующую таблицу с двумя входами

	T0	T1	S	М	L
fi	( + или –)	( + или –)	( + или –)	( + или –)	( + или –)
…	…	…	…	…	…

В соответствующей клетке таблицы ставится "+", если функ­ция, отмеченная в строке, принадлежит классу, отмеченному в столбце и "–" в противном случае. Очевидно, рассматриваемая систе­ма функций F будет полной, если в каждом столбце построенной таблицы будет, по крайней мере, один минус.

Пример.Рассмотрим систему 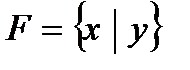, состоящую из од­ной функции Шеффера, и проверим, является ли она полной.

1. Согласно таблице истинности функции Шеффера, она не сохраняет ни ноль, ни единицу, то есть .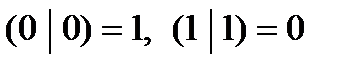

2. 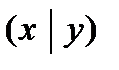не является самодвойственной, так как .

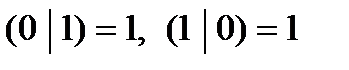3. 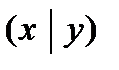не является монотонной, так как, например, .

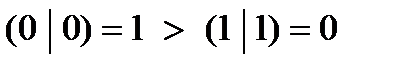4. 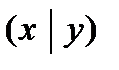не является линейной, так как отлична от линейных функций от двух переменных: .

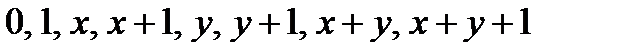Таким образом, соответствующая таблица для имеет во всех столбцах минусы. Поэтому система 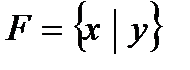является полной.

Определение 12. Система булевых функций называется базисом, если она полна, а удаление любой функции из этой системы делает ее неполной.

Теорема 7. Каждый базис содержит не более четырех булевых функций.

Упражнение. Доказать, что следующие системы булевых функций являются базисами:

.

2.3. Приложение булевых функций
к анализу и синтезу релейно-контактных схем

Булевы функции широко применяются при описании работы дискретных управляющих систем, при исследовании некоторых электрических цепей, так называемых релейно-контактных схем.

Под релейно-контактной схемой (РКС) понимается устройство из проводников и двухпозиционных контактов. Оно может быть предназначено, например, для соединения или разъединения полюсов источника тока с некоторым потребителем. Контакты РКС могут быть двух типов: замыкающие и размыкающие. Каждый контакт подключен к некоторому реле (переключателю). Когда реле срабатывает, все подключенные к нему замыкающие контакты замкнуты, а размыкающие контакты разомкнуты; в противном случае наоборот. Каждому реле ставится в соответствие своя булева переменная x, которая принимает значение 1, если реле срабатывает, и 0 в противном случае.

Замыкающие контакты, подключенные к реле x, обозначаются символом x, а размыкающие – символом 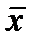. Это означает, что при срабатывании реле x все его замыкающие контакты x проводят ток и им сопоставляется 1, а все размыкающие контакты 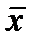не проводят ток и им сопоставляется 0. При отключении реле создается противоположная ситуация.

Всей схеме ставится в соответствие булева переменная f, которая равна 1, если схема проводит ток, и 0 в противном случае. Переменная f, соответствующая схеме, очевидно, является функцией от переменных 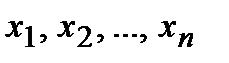, соответствующих реле. Эта функция называется функцией проводимости схемы, а ее таблица – условиями работы схемы. Две РКС называются равносильными, если они обладают одинаковыми функциями проводимости. Из двух равносильных схем более простой считается та, которая содержит меньшее число контактов.

При рассмотрении РКС возникают два типа задач: анализ и синтез. Задача анализа состоит в описании ра­боты схемы. Задачей синтеза является построение РКС по заданному описанию рабо­ты. При решении этих задач успешно используется аппарат функций алгебры логики. Последовательное соединение контактов записывают как конъюнкцию соответствующих переменных, а параллельное соединение двух контактов как дизъюнкцию этих переменных. Это вполне согласуется с обычным пониманием проводимости между полюсами.

Пример.По заданной РКС найти ее функцию проводимости.

x

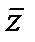
y

x

y

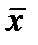
y

z

Схема состоит из трех параллельных ветвей. Первая ветвь, в свою очередь, состоит из двух параллельных ветвей, в одной из которых последовательно соединены два контакта x и 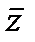, а в другой имеется один контакт y. Поэтому первая параллельная ветвь имеет следующую функцию проводимости: .

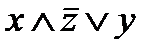Вторая параллельная ветвь РКС состоит из двух последовательно соединенных контактов x и y и поэтому имеет функцию проводимости: .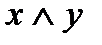

Третья параллельная ветвь состоит из двух параллельных ветвей, в одной из которых один контакт 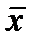, а в другой последовательно соединены y и z. Поэтому функция проводимости следующая: .

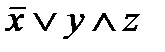Для нахождения функции проводимости всей схемы нужно построить дизъюнкцию найденных функций:

.

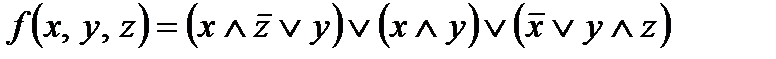Поскольку всякая булева функция может быть выражена через конъюнкцию, дизъюнкцию и отрицание, то и всякая функция может быть реализована с помощью РКС, то есть может быть построена такая схема, для которой данная функция служит функцией проводимости.

3. Исчисление высказываний

Применительно к алгебре высказываний (АВ) аксиоматический подход состоит в следующем. Из всех формул алгебры высказываний выделяется некоторая часть. Формулы из этой части объявляются аксиомами. Определяется некоторое правило, по которому из одних формул можно получать новые формулы. Аксиомы выделяются, и правило определяется так, что по нему из аксиом могут быть получены все тавтологии алгебры высказываний. Таким образом, тавтологии алгебры высказываний оказываются теоремами аксиоматической теории. В результате получаем аксиоматическое построение алгебры высказываний.

В качестве системы аксиом могут быть выбраны разные части совокупности всех формул АВ. То же относится к правилам получения новых формул. В зависимости от выбора получаются различные аксиоматизации АВ. Общим для них является то, что все они обладают одним и тем же множеством теорем – это совокупность всех тавтологий АВ.

Рассмотрим одну из возможных аксиоматизаций.

Сначала дадим общее определение аксиоматической тео­рии.

Определение 1.Будем считать, что аксиоматическая теория T за­дана, если выполнены следующие условия:

1)задано некоторое множество символов теории T; причем конеч­ные последовательности символов называются выражениями теории T;

2) определено некоторое подмножество выражений, называемых формулам;

3) выделено некоторое подмножество формул, называемых аксио­мамитеории T;

4) имеется некоторое множество правил, которые позволяют из од­них формул теории T получать другие.

Определение 2. Выводом в T называется последовательность фор­мул 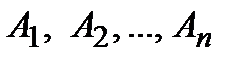такая, что для любого i формула A_i есть либо аксиома теории Т, либо непосредственное следствие каких-либо предыдущих формул по одному из правил вывода.

Определение 3.Формула А теории T называется теоремой (или выводимой формулой), если существует вывод в T, в котором по­следней формулой является формула А.

Определение 4.Формула А называется следствием множества формул F в T тогда и только тогда, когда существует такая после­довательность формул 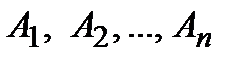, что А_n совпадает с А и для любого i A_i есть либо аксиома, либо элемент F, либо непосредственное след­ствие некоторых предыдущих формул. Элементы F называются ги­потезами вывода.

В дальнейшем для сокращения утверждения "А есть следствие F" мы будем употреблять обозначение F├ А. В частности, ├ А служит сокращением утверждения "А есть теорема".

Введем теперь аксиоматическую теорию L для исчисления высказы­ваний.

1. Символами L являются , ®, (, ) и буквы латинского алфавита с целыми положительными числами в качестве индексов. Символы , ® называются логическими связками,а буквы латинского алфа­вита с индексами – пропозициональными переменными.

2. Каждая пропозициональная переменная есть формула. Если А, В – формулы, то 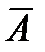и 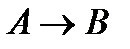– тоже формулы.

3. Каковы бы ни были формулы А, В и С теории L, следующие фор­мулы суть аксиомы L:

(А1) ;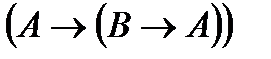

(А2) ;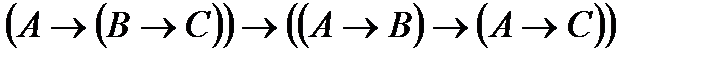

(A3) .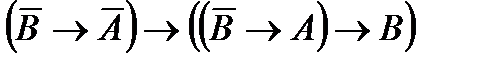

4. Правилами вывода служат правило подстановки и правило заключения (или modus ponens, или сокращенно МР). Правило подстановки заключается в следующем. Пусть F – формула, содержащая букву А. Тогда, если F выводимая формула, то, заменив в ней букву А всюду, где она входит, произвольной формулой G, мы также получим выводимую формулу. Согласно правилу заключе­ния, если 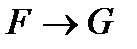и F – выводимые формулы, то G – также выводимая формула.

Пример 1.Покажем, что 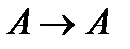выводимая формула.