Недетерминированный алгоритм решения множества уравнений
Вход: множество уравнений 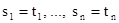 .
.
Выход: множество уравнений в разрешённой форме 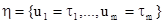 .
.
Действия: пока истинно условие применимости хотя бы одного из перечисленных далее преобразований, выполнять в цикле альтернативы.
Начало цикла:
I. если существует уравнение вида: t = x, где t – не переменная, а x – переменная, то заменить это уравнение на x = t; в противном случае
II. если существует уравнение вида: x = x, где x – переменная, то удалить это уравнение из системы уравнений; в противном случае
III. если существует уравнение вида: s = t, в котором s и t не являются переменными, то если корневые функции термов s и t различны, тогда возвращается «отказ», в противном случае осуществить преобразование редукции термов;
IV. если существует уравнение вида: x = t, такое, что переменная x не входит в другие уравнения системы и терм t отличен от x, то если переменная x входит в t, тогда возвращается «отказ», в противном случае осуществить преобразование элиминации переменной.
Конец цикла. (Возвращается «успех», преобразованная система уравнений будет искомым унификатором.)
Здесь под элиминацией переменной понимается переход от системы уравнений к системе, полученной после подстановки x = t.
Пример
Рассмотрим систему, состоящую из одного уравнения:
((a Ç b) È d) È (a Ç b) = (c È (a Ç b) È (a Ç b)}
1) Применяем случай III, делаем редукцию, получаем: h = {(a Ç b) È d) = c È (a Ç b), a Ç b = a Ç b}.
2) Применяем случай III, получаем: h = {a Ç b = с, d = a Ç b, a Ç b = a Ç b}.
3) Применяем случай III для последнего уравнения и повторяем 2 раза случай II, это приводит к h = {a Ç b = с, d = a Ç b}.
4) Применяем случай I, получаем ответ: h = {c = a Ç b, d = a Ç b}.
Предикаты и отношения
Функция n переменных, принимающая значения 0 и 1, называется n-местным предикатом. Каждому отношению 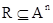 соответствует предикат, равный характеристической функции подмножества R. Ясно, что определение n-местного предиката
соответствует предикат, равный характеристической функции подмножества R. Ясно, что определение n-местного предиката 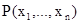 на множестве А равносильно заданию отношения:
на множестве А равносильно заданию отношения:
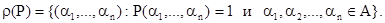
Пусть 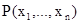 и
и 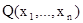 – предикаты. Конъюнкцией P и Q называется предикат
– предикаты. Конъюнкцией P и Q называется предикат 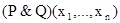
 , дизъюнкцией – предикат
, дизъюнкцией – предикат  , отрицание определяется с помощью предиката
, отрицание определяется с помощью предиката  .
.
Для предикатов определяются кванторы существования и всеобщности. Пусть 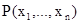 – n-местный предикат. Запись:
– n-местный предикат. Запись: 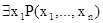 означает, что существует
означает, что существует 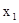 , для которого
, для которого 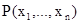 =1, запись:
=1, запись: 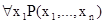 означает, что
означает, что 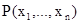 =1 для всех
=1 для всех 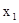 . Аналогично определяются предикаты
. Аналогично определяются предикаты 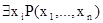 и
и  , при
, при 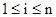 . В этих случая говорят, что переменная
. В этих случая говорят, что переменная 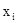 связана квантором. Предикаты
связана квантором. Предикаты 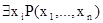 и
и  будут зависеть от n-1 переменных. В случае, когда
будут зависеть от n-1 переменных. В случае, когда  , положим
, положим 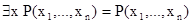 и
и  . Тем самым мы определим предикаты
. Тем самым мы определим предикаты  и
и  для любых символов переменных x. Отношение, соответствующее предикату
для любых символов переменных x. Отношение, соответствующее предикату 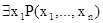 будет проекцией отношения, определяемого P, на область
будет проекцией отношения, определяемого P, на область 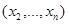 , оно будет равно объединению по всем aÎA отношений, определяемых предикатами
, оно будет равно объединению по всем aÎA отношений, определяемых предикатами 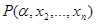 . Предикату
. Предикату 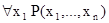 соответствует отношение, равное пересечению этих отношений. Таким образом,
соответствует отношение, равное пересечению этих отношений. Таким образом,
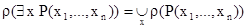 ;
;
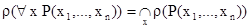 .
.
Язык логики предикатов
Определим синтаксис языка первого порядка. Алфавит языка первого порядка состоит из логических символов Ú, Ø, $, =, из символов переменных  и из нелогических символов. К логическим символам отнесём символы скобок и запятой. В качестве символов переменных будем использовать также x, y, z, u, v и т.д. Логические символы одинаковы для всех языков первого порядка. Нелогическими называются символы операций, символы предикатов и символы констант. Язык первого порядка L задаётся как множество нелогических символов. Если L = Æ, то L называется языком чистого равенства.
и из нелогических символов. К логическим символам отнесём символы скобок и запятой. В качестве символов переменных будем использовать также x, y, z, u, v и т.д. Логические символы одинаковы для всех языков первого порядка. Нелогическими называются символы операций, символы предикатов и символы констант. Язык первого порядка L задаётся как множество нелогических символов. Если L = Æ, то L называется языком чистого равенства.
Каждому s Î L ставится в соответствие #(s) Î w. Если s – константа, то #(s) = 0. Если R – символ предиката, такого, что #(R) = n, то R называется символом n-местного предиката. Если f – символ операции, и #(f) = n, то f называется символом n-арной операции. Для предикатов и операций число #(R) (соответственно #(f)) больше 0, и оно называется местностью (соответственно арностью). Объединение множеств символов операций и констант составляет множество функциональных символов, позволяющее строить термы языка L на множестве 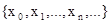 .
.
К предикатам языка L мы всегда относим бинарный предикат 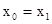 (равенство). Определим формулы языка L.
(равенство). Определим формулы языка L.
Атомной формулой языка L называется выражение вида:  , где
, где  – термы языка L, а R Î L – символ n-местного предиката. В частности, выражение
– термы языка L, а R Î L – символ n-местного предиката. В частности, выражение 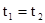 будет атомарной формулой для любых термов языка L. Множество всех формул языка L определяется как наименьшее множество выражений, которое содержит все атомные формулы и удовлетворяет условиям: если q и y – формулы, а x – переменная, то выражения
будет атомарной формулой для любых термов языка L. Множество всех формул языка L определяется как наименьшее множество выражений, которое содержит все атомные формулы и удовлетворяет условиям: если q и y – формулы, а x – переменная, то выражения  , Øq, $xq – формулы. Формулы q и y называются подформулами формулы
, Øq, $xq – формулы. Формулы q и y называются подформулами формулы  , формула q – подформулой формул Øq и $xq.
, формула q – подформулой формул Øq и $xq.
Будем предполагать, что другие логические связки служат сокращениям:
(q & y) для Ø(Øq Ú Øy),
(q ® y) для (Øq Ú y),
" x q для Ø$ x Øq.
Формула Øx = y обычно записывается как x ¹ y. Примеры формул:
" x $ y P (x, y, x È z), $ x (y £ x ® y = x).
Замена переменных
Переменная, содержащаяся в формуле, называется свободной, если она не связана квантором, в противном случае она называется связанной. Переменная может входить в формулу несколько раз, в этом случае аналогичные определения применяются к каждому вхождению. Например, в формуле
" y (y = z) ® $ z (z < x)
первое вхождение переменной z свободно, а второе – связанное. Переменная x является свободной, а y – связанной. Формальное определение свободных и связанных переменных следующее:
1) все вхождения переменных в атомных формулах свободны;
2) свободные вхождения x в Øq есть в точности свободные вхождения x в q;
3) свободные вхождения x в  состоят из свободных вхождений x в q и свободных вхождений x в y;
состоят из свободных вхождений x в q и свободных вхождений x в y;
4) если x и y – различные переменные, то свободные вхождения x в формулу
$ y q соответствуют свободным вхождениям x в формулу q;
5) в формуле $ x q нет свободных вхождений переменной x.
Запись: q(x) указывает на то, что формула q содержит свободные вхождения переменной x. Если c – символ константы, то q(с) означает формулу, полученную заменой всех свободных вхождений x в q на с. Например, если q(x) = $y((y = x) & " x (x = y)), то q(c) = $y((y = c) & " x (x = y).
Мы пишем: 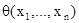 для указания того, что q содержит свободные переменные среди
для указания того, что q содержит свободные переменные среди  . Применяется запись:
. Применяется запись: 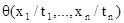 для обозначения формулы, в которой все свободные вхождения каждой из переменных
для обозначения формулы, в которой все свободные вхождения каждой из переменных 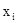 формулы q заменяются на терм
формулы q заменяются на терм  ,
, 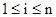 . Таким образом, q(с) является сокращением обозначения q(х/с).
. Таким образом, q(с) является сокращением обозначения q(х/с).
Формула, не содержащая свободных переменных, называется предложением.
Может случиться, что при замене переменной термом нарушается очевидный принцип, согласно которому замена переменной в равных формулах даёт равные формулы. Например, пусть t = f(y), q(z) = $y(y < z). Тогда после замены получаем: 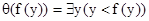 . С другой стороны, q(z) = $x(x < z), и, значит,
. С другой стороны, q(z) = $x(x < z), и, значит, 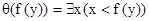 . Получаем не равные формулы. Поэтому перед подстановкой терма
. Получаем не равные формулы. Поэтому перед подстановкой терма 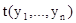 в формулу q(х) связанные переменные, содержащиеся в
в формулу q(х) связанные переменные, содержащиеся в  будем переименовывать на символы, не встречающиеся в
будем переименовывать на символы, не встречающиеся в  .
.
Другой выход следующий: терм t называется свободным для переменной x в формуле q(х), если никакое свободное вхождение x в q не лежит в области действия кванторов  и
и 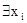 , где
, где 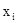 входит в t. В этом случае замена q(х/t) допускается.
входит в t. В этом случае замена q(х/t) допускается.
При подстановках констант противоречия не возникают.
Замечание. Применяемые в анализе и алгебре обозначения: 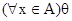 и
и 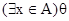 служат сокращениями соответственно формул
служат сокращениями соответственно формул 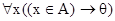 и
и 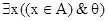 . Например,
. Например,  будет определяться формулой:
будет определяться формулой: 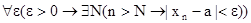 .
.
Исчисление предикатов
Для того чтобы определить формальную теорию, связанную с языком первого порядка, введём логические аксиомы и правила вывода языка L. Логические аксиомы подразделяются на 3 группы:
1) Аксиомы предложений: всякая формула q языка L, которая может быт получена из некоторой тавтологии исчисления высказываний K (описанного в разд. 3 с помощью аксиом К1 – К10) в результате подстановки формул языка L на место высказывательных символов, есть логическая аксиома языка L. Всякая такая формула называется тавтологией языка первого порядка L.
2) Аксиомы кванторов
· если q и y – формулы языка L, то имеют место следующие аксиомы:
("x (q ® y)) ® (q ® "x y), если х не входит свободно в q;
("x (q ® y)) ® (($ x q) ® y), если х не входит свободно в y;
· для каждой формулы q(х) и терма t, свободного для x, имеют место кванторные аксиомы:
" х q(х) ® q(t);
q(t) ® $ х q(х).
3) Аксиомы равенства
t = t для любого терма t;
(t = s) & q(t) ® q(s), для любых формул q(х) и термов s, t, для которых х свободна в q, а s и t свободны для х (здесь q(t) означает формулу q(x/t)).
Правила вывода
(MP) Из формул q и q ® y выводится y (Modus Ponens).
(Gen) Из формулы q выводится " x q (правило обобщения).
Таким образом, определена формальная теория, (разд.3.4), в которой есть формулы, аксиомы и правила вывода. Эта теория называется исчислением предикатов L.
Запись: å  q означает, что существует вывод формулы q из логических аксиом и формул из множества å. Если Æ
q означает, что существует вывод формулы q из логических аксиом и формул из множества å. Если Æ  q, то q – теорема исчисления предикатов L. Множество å называется противоречивым, если для каждой формулы q языка L существует вывод: å
q, то q – теорема исчисления предикатов L. Множество å называется противоречивым, если для каждой формулы q языка L существует вывод: å  q. В противном случае å называется непротиворечивым. Предложение q называется непротиворечивым, если множество {q} непротиворечиво. Множество формул å называется максимально непротиворечивым, если оно не является собственным подмножеством некоторого непротиворечивого множества.
q. В противном случае å называется непротиворечивым. Предложение q называется непротиворечивым, если множество {q} непротиворечиво. Множество формул å называется максимально непротиворечивым, если оно не является собственным подмножеством некоторого непротиворечивого множества.
Легко доказать следующие свойства непротиворечивых множеств:
1) Множество å непротиворечиво, если и только если каждое его конечное подмножество непротиворечиво.
2) Пусть q – предложение. Тогда множество å È {q} противоречиво, если и только если å  Øq.
Øq.
3) Пусть å – максимально непротиворечивое множество. Тогда для любых предложений q и y имеет место:
(i) å  q, если и только если q Î å;
q, если и только если q Î å;
(ii) q Ï å, если и только если Øq Î å;
(iii) (q & y) Î å, если и только если q Î å и y Î å;
4) Каждое непротиворечивое множество предложений содержится в некотором максимальном непротиворечивом множестве предложений.
Теорема (о непротиворечивости исчисления предикатов). Нет формул q исчисления предикатов L, для которых существуют выводы:  q и
q и  Øq.
Øq.
Доказательство. Каждой формуле q поставим в соответствие формулу h(q) исчисления высказываний K, множество символов P которого состоит из предикатов RÎL. Формулу h(q) определим по индукции:
1) 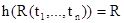 для атомных формул;
для атомных формул;
2)  ,
, 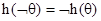 ,
,
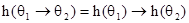 ,
,
 , для любых формул
, для любых формул 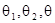 ;
;
3) h("xq) = h(q), h($xq) = h(q).
Для всякой логической аксиомы q формула h(q) будет тавтологией в K. Если бы для некоторой формулы q существовали выводы  q и
q и  Øq, то формулы h(q) и Øh(q) были бы тавтологиями в исчислении высказываний. Поскольку исчисление высказываний непротиворечиво, это невозможно. Стало быть, нет формул q, для которых существуют выводы:
Øq, то формулы h(q) и Øh(q) были бы тавтологиями в исчислении высказываний. Поскольку исчисление высказываний непротиворечиво, это невозможно. Стало быть, нет формул q, для которых существуют выводы:  q и
q и  Øq.
Øq.
