Понятие о логической функции и цифровом устройстве. Переключательные функции одной и двух переменных

В цифровой технике для обозначения понятий, предметов, действий пользуются кодовыми словами. «Кодовое» слово в цифровой технике есть определенной длины последовательность символов «0» и «1». Если длина кодовых слов составляет n разрядов, то можно построить 2ⁿ различных комбинаций – кодовых слов.

Информация, которая передается между отдельными узлами (блоками) сложного цифрового устройства, представляется в виде кодовых слов. Таким образом, на входы каждого узла поступают кодовые слова, на выходе узла образуется новое кодовое слово, представляющее собой результат обработки входных слов. Выходное слово зависит от того, какие слова поступают на входы узла. Поэтому можно говорить, что выходное слово есть функция, для которой аргументами являются входные слова. Если аргументы и функция могут принимать значения «лог. О» и «лог. 1», будем эти функции называть функциями алгебры логики (ФАЛ).

Устройства, предназначенные для формирования функций алгебры логики, называются логическими устройствами или цифровыми устройствами. Цифровые устройства (либо их узлы) можно делить на типы по различным признакам.

По способу ввода и вывода кодовых слов различают логические устройства последовательного, параллельного и смешанного действия.

На входы устройства последовательного действия символы кодовых слов поступают не одновременно, а последовательно во времени, сим­вол за символом (в так называемой последовательной форме). В такой же последовательной форме выдается выходное слово.

На входы устройства параллельного действия все n символов каждо­го входного кодового слова подаются одновременно (в так называемой параллельной форме). В такой же форме образуется на выходе выходное слово.

В устройствах смешанного действия входные и выходные кодовые слова представляются в разных формах. Например, входные слова – в последовательной форме, выходные – в параллельной форме.

По способу функционирования логические устройства (и их схемы) делят на два класса: комбинационные устройства (и соответственно комбинационные схемы) и последовательностные устройства (последовательностные схемы).

В комбинационном устройстве (называемом также автоматом без памяти) каждый символ на выходе «лог. О» или «лог. 1» определяется лишь символами «лог. О» или «лог.1», действующими в данный момент времени на входах устройства, и не зависит от того, какие символы ранее действовали на этих входах. В этом смысле комбинационные устройства лишены памяти (они не хранят сведений о прошлом работы устройства).

В последовательностных устройствах (или автоматах с памятью) выходной сигнал определяется не только набором символов, действующих на входах в данный момент времени, но и внутренним состоянием устройства, а последнее зависит от того, какие наборы символов действовали на входах во все предшествующие моменты времени в процессе работы устройства. Поэтому можно говорить, что последовательностные устройства обладают памятью (они хранят сведения о прошлом работы устройства).

Логические функции, также как и математические, могут задаваться аналитически (в виде логического выражения) и табличным способом. Таблицы для логических функций называют таблицами истинности. Таблица истинности позволяет определять значение функции для любых значений аргументов.

Если число аргументов функции равно n, то число различных сочетаний (наборов) значений аргументов составляет 2ⁿ. Если число аргументов функции равно n, то можно составить 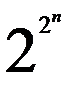различных функций.

Существует 4 функции одного аргумента. Функции одного аргумента представляются следующими выражениями:

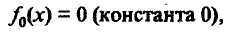
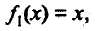
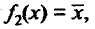
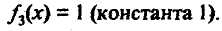
Для двух аргументов существует 16 логических функций. Среди которых главными являются дизъюнкция и конъюнкция.

Дизъюнкция переменных Х₁, Х₂ равна единице, когда Х₁ или Х₂ или оба аргумента равны единице.

Конъюнкция переменных Х₁, Х₂ равна единице, когда Х₁ и Х₂ равны единице.

Функции двух аргументов представлены в таблице 2.1.1.

Таблица 2.1.1

Таблица истинности	Как читается	Название операции
Х1
Х2
Х1* Х2 X1&X2 X1 X2					Х1 и Х2	Конъюнкция; логическое И; логическое произведение
Х1 Х2			]		Х1 или Х2	Дизъюнкция; логическое ИЛИ; логическая сумма
Х1 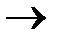Х2					Х1 влечет Х2; Х1имплицируетХ2	Импликация
Х1 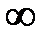Х2					Х1, эквивалентно Х2	Эквивалентность равнозначность
Х1 Х2					либо Х1, либо Х2; Х1 неэквивалентно Х2	Сумма по модулю 2; неравнозначность; исключающее ИЛИ
Х1 Х2					Х1 запрет по Х2; Х1 но не Х2 .	Запрет; отрицание импликации
Х1 / Х2					Х1 и Х2 несовместны	Логическое И-НЕ; элемент (штрих) Шеффера; отрицание конъюнкции
Х1 Х2					ни Х1 ни Х2	Логическое ИЛИ-НЕ; стрелка Пирса; функция Вебба; отрицание дизъюнкции
х			не Х	Логическое НЕ;
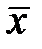					инверсия; логическое отрицание

В таблице 2.1.2 представлены функциональные обозначения логических элементов, выполняющих основные логические функции.

Таблица 2.1.2

«ИЛИ»	«И»	«ИЛИ-НЕ»	«И-НЕ»	Исключающее «ИЛИ»	«НЕ»

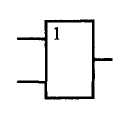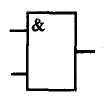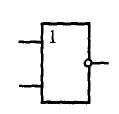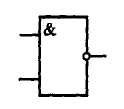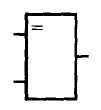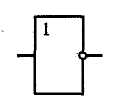В таблице 2.1.3 приведены таблицы истинности всех функций двух аргументов.

Таблица 2.1.3

Аргументы

Функции

Х1

Х2

F0

F1

F2

F3

F4

F5

F6

F7

F8

F9

F10

F11

F12

F13

F14

F15

о

Из таблицы видим, что указанные функции соответствуют логическим выражениям:

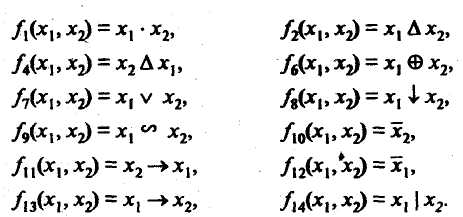
Остальные из приведенных в таблице 1.4 функций не представляют практического интереса: f₀ (x₁, x₂)=0, f₃ (x₁, x₂)= x₁, f₅ (x₁, x₂)= x₂, f₁₅ (x₁, x₂)=1.