Г). Классификация. Операции с классами.

Частным, но очень распространенным способом деления понятий по видообразующему признаку является классификация. Классификация (лат. classis - разряд, fatio - делаю) - это разделение по наиболее существенным признакам предметов какого-либо рода на взаимосвязанные группы, каждая из которых, обладая общими родовыми признаками, занимает свое определённое постоянное место благодаря наличию своих собственных, только ей свойственных, признаков.

Классическим примером научной классификации является периодическая система химических элементов Д.И.Менделеева (1834-1907 гг.), составленная по гениально найденному признаку, а именно - по возрастанию атомного веса элементов. Исходя из открытого им периодического закона, Д.И. Менделеев оставил в своей таблице элементов пустые места, которые в дальнейшем были заполнены вновь открытыми элементами. При этом предсказанные ученым свойства элементов совпали со свойствами, открытыми опытным путем после того, как элементы были найдены. Периодическая таблица элементов во времена Менделеева заканчивалась на элементе № 92 - уране; считали, что ничего тяжелее урана в природе нет. Сегодня таблица насчитывает более ста элементов и открытия продолжаются.

Итак, любая классификация суть деление, но обратного никак сказать нельзя. Всякое деление может быть произведено для какой-либо сиюминутной цели, и оно отбрасывается, теряя свое значение, как только эта цель достигнута. Так, вор-карманник, находясь в переполненном троллейбусе, для исполнения своего преступного намерения мысленно группирует находящихся в данном троллейбусе людей на определенные виды, выделяя среди них потенциальных жертв. И данное деление для него перестаёт существовать после исполнения (удачного или неудачного) преступного замысла.

Классификация же, будучи однажды создана, получает устойчивый характер, сохраняется до тех пор, пока новые данные, новые знания не потребуют (коренного или плавного, уточняющего) её изменения. При этом классификация, как правило, представляет собой не просто двухчленное или многочленное деление - каждый член классификации, в свою очередь подвергается дальнейшему делению, вплоть до нахождения самых низших классов. Так, согласно ст. 15 УК РФ, все преступления делятся на 4 категсрии: 1) небольшой тяжести (наказание до 2-х лет лишения свободы
2) средней тяжести (наказание до 5 лет лишения свободы); 3) тяжкие (наказание до 10 лет лишения свободы); 4) особо тяжкие (наказание на срок свыше 10 лет и более строгое наказание).

Каким условиям должна удовлетворять хорошая классификация? Ясно, что она должна отвечать всем правилам деления, а как истинно научный способ деления она должна быть исчерпывающей и исключающей. Исчерпывающей она является тогда, когда сумма объёмов классов равна объёму родового понятия. Особенность классификации состоит во взаимоисключении объёмов классов, т.е. в том, чтобы ни один из элементов делимого объёма родового понятия не находился одновременно в двух разных объёмах классов.

Исчерпывающую и исключающую классификацию можно получить только в случае деления по принципу дихотомии и по контрадикторным (противоречащим) признакам. В этом случае деление является «многоэтажным». Данный объём родового понятия делим на два, каждый из образовавшихся или один из них вновь делим на два, каждый из вновь образовавшихся или некоторые, или только один из них - снова на два и т.д. Такую классификацию можно прервать на любом уровне, и результат её будет всегда правильным. Основание деления здесь без всякого риска можно

менять на любом «этаже».

Так, жителей данного города можно делить на совершеннолетних и несовершеннолетних, затем выделить среди первой группы женщин и мужчин, далее совершеннолетних мужчин разделить на подданных данного государства и иностранцев, разделив, в свою очередь, неиностранцев на призывников и непризывников. В результате образовалась следующая классификация: жители несовершеннолетние; женщины совершеннолетние; мужчины совершеннолетние - подданные данного государства и они же подлежащие призыву в армию; мужчины совершеннолетние - подданные и они же не подлежащие призыву. Легко убедиться, что любой житель данного города должен входить в одну из указанных групп и никто из них не входит в две группы одновременно.

Следует иметь в виду, что не только таксономическое, но и мереологическое деление может оказаться многоуровневым, напоминающим классификацию, когда оно проводится последовательно, как говорят, «до последнего винтика»

Подводя промежуточный итог, следует отметить, что деление понятий, классификация, как средства научного анализа, помогают правильно распределить предметы по группам, изучить их, а следовательно, глубже познать весь класс выделенных предметов в целом.

Будущему юристу важно знать и уметь осуществлять основные логические операции с классами (объёмами понятий). К этим операциям относятся: объединение классов (сложение), вычитание классов, пересечение классов (умножение), образование дополнений к классам (отрицание).

В операциях с классами приняты следующие обозначения: А,В, С,... — произвольные классы, 1 — универсальный класс, 0 — нулевой (пустой) класс, знак « » обозначает объединение классов (сложение), знак « ».— пересечение классов (умножение), А (не-А)— дополнение к классу А(отрицание). В операциях с классами обычно используются круговые схемы (круги Эйлера), универсальный класс обозначается прямоугольником.

Операция объединения классов (сложение)состоит в объединении двух или нескольких классов в один класс, состоящий из всех элементов, входящих в слагаемые классы.

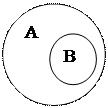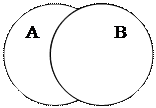Рис. а Рис. б

Операция объединения классов записывается с помощью знака сложения АВ.Множество, полученное в результате сложения, называется суммой (на схеме полученное множество заштриховано). Складывать можно множества, находящиеся в любых отношениях, например множества, входящие в понятия, находящиеся в отношении подчинения: «юрист» (В) и «следователь» (А).Множество, полученное в результате сложения, включает юристов-следователей и юристов-неследователей (рис. а). Объединяя
классы, находящиеся в отношении частичного совпадения: «юрист» (А)и «депутат Государственной Думы» (В), — получим множество, объединяющее юристов-недепутатов (1), юристов-депутатов (2) и депутатов-неюристов (3) — рис. б.

Операция вычитания классовдает класс, состоящий из элементов, исключающих элементы вычитаемых классов. Вычитая, например, элементы класса «следователь» (А)из класса «юрист» (В), получаем класс юристов не-следователей (рис. в). Вычитая элементы класса «юрист» (А)из класса «депутат Государственной Думы» (В), получаем класс депутатов Государственной Думы, не являющихся юристами. Множество, полученное в результате вычитания классов, заштриховывается (рис. г).

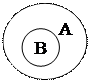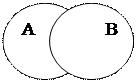Рис. в Рис. г

Операция пересечения классов (умножение)состоит в отыскании элементов, общих для двух или нескольких классов (множеств). Так, в результате умножения множеств, мыслящихся в понятиях «юрист» (А)и «депутат» (В), получаем новое множество: юристов-депутатов (рис. д).

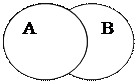Рис. д

Операция пересечения классов записывается с помощью знака умножения: АВ. Множество, полученное в результате умножения, называется произведением (заштрихованная часть схемы). Умножать можно три и больше множеств. Так, умножая множества, входящие в понятия «юрист» (А),«депутат» (В) и «москвич» (С),получаем множество юристов, являющихся депутатами и москвичами (рис. е).

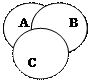Рис. е

При умножении множеств, входящих в несовместимые понятия, например, «следователь» и «адвокат», получаем нулевой (пустой) класс, так как элементов, входящих одновременно в оба понятия, не существует.

Образование дополнения (отрицание).Дополнением к классу Аназывается класс не-А (А'),который при сложении с Аобразует универсальную область. Эта область представляет собой универсальный класс и обозначается знаком «1». Чтобы образовать дополнение, нужно класс Аисключить из универсального класса: 1 - А = А'.

Образование дополнения состоит, таким образом, в образовании нового множества, путём исключения данного множества из универсального класса, в который оно входит. Так, исключая множество адвокатов (А) из универсалного класса юристов (1), образуем дополнение: множество юристов-неадвокатов (А). В своей сумме оба понятия образуют весь универсальный класс, соответствующий понятию «юрист» (рис. д).

Рис. д

Заключая рассмотрение вопросов лекции, ещё раз подчеркнём, что понятие является исходной формой абстрактного мышления, способной замещать или представлять предметы, вводить их в систему более сложных связей и отношений. Именно понятия составляют основу других форм абстрактного мышления - суждений и умозаключений.

* * *

Слово «понятие» однокоренное со словом «понимание». И когда мы выходим на философский уровень их рассмотрения, то, в числе прочих, могут возникать два следующих проблемных вопроса: первый, как тесно связанный с формально-логическим аспектом осмысления понятия и в свою очередь распадающийся на ряд подвопросов – когда же мы в итоге имеем дело с понятием? Когда называем его имя? Когда раскрываем его содержание и объём? Или понятие – это всё вместе взятое?

И второй вопрос, также распадающийся на ряд подвопросов: - что значит, в конце концов, понимание того, что, например, является правом? Кто выступает основным субъектом этого понимания? Бог, законодатель, учёный …? И существуют ли какие-либо границы в процессах понимания?

В связи с проблемой понимания текстов как, основных исторических свидетельств нашей мыследеятельности, в философии возникает целое направление, под именем «герменевтика». Мне же хотелось бы высказать некоторые самые общие соображения.

В связи с ответом на первый вопрос представляется достаточно очевидным, что понятие не только его имя, содержание и объём. Хотя, в формально-логическом аспекте рассмотрения, прежде всего, это. Как форма мышления понятие отражает явления объективно существующей действительности посредством выделения их общих, существенных, отличительных признаков. Но даже формально-логическая сторона осмысления понятия этим не исчерпывается. Понятие предполагает и системное видение объектов осмысления, и понимание их взаимосвязанности с другими явлениями, и бесконечной собственной сложности, и даже просто внешнее представление о множестве контекстуальных вариантов употребления имени понятия. То есть основной смысл ответа на первый вопрос заключается в том, что понятие – это не только его имя, содержание и объём, тем более не только его отдельный структурный компонент или аспект рассмотрения, а всё в единстве, в том числе, возможно и не явно осмысленное соединение конкретной понятийной области со всей совокупностью знаний познающего субъекта.

Ответ на второй вопрос, на мой взгляд, можно дать по аналогии с ответом на вопрос – что есть истина? Всматриваясь и вдумываясь в одно и тоже определение понятия права, каким глубоким и правильным оно бы не было, два разных человека вынесут своё понимание, поскольку на это понимание окажет влияние и общее мировоззрение человека, и уровень его образования, и конкретный жизненный опыт, и мыслительные способности, и, подчас, неизвестно, что ещё.

Идеал абсолютно истинного и полного определения чего-либо вряд ли достижим. Это прекрасно понимали уже философы древнего мира. Демокрит говорил, что полное причинное объяснение даже одного явления он бы предпочёл персидскому престолу. В мире всё взаимосвязано и всё отражает всё. В капле воды отражается океан. «Познай самого себя – и ты познаешь богов и вселенную». Именно эти мировоззренческие установки приводили наиболее глубоких мыслителей к неутешительному – «я знаю, что я ничего не знаю». Тем самым давайте довольствоваться «синицей в руке», истиной относительной: ибо она тоже в русле пути к истине абсолютной и представляет её. К тому же созвучное времени и уровню развития научного знания понимание чего-либо в форме истины относительной – тоже есть нелёгкий труд. Для студента это процесс обучения, изучения логики, других образовательных дисциплин.