Дискретные бинарные изображения

До сих пор мы рассматривали непрерывные бинарные изображения, определенные во всех точках плоскости. Должно быть очевидным, что при переходе к дискретным изображениям интегралы становятся суммами. Например, площадь вычисляется (в единицах площади элемента изображения) в виде суммы

,

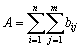где 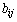— значение бинарного изображения в точке, находящейся в 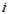–й строке и 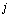–м столбце. Здесь мы полагали, что поле изображения разбито на квадратную решетку с т столбцами и п строками.

Часто изображение просматривается строка за строкой в той же самой последовательности, в какой телевизионный луч бежит по экрану (если не учитывать того, что четные строки считываются вслед за нечетными). Как только считано значение очередного элемента изображения, проверяем равенство 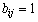. Если оно выполняется, добавляем 1, 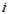, , 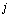, 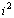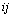и 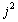кнакапливаемым значениям площади, первых моментов и вторых моментов. По окончании цикла сканирования с помощью этих значений легко найти площадь, положение и ориентацию.