Тригонометрические вычисления
В Microsoft Excel можно выполнять как прямые, так и обратные тригонометрические вычисления, то есть, зная значение угла, находить значения тригонометрических функций или, зная значение функции, находить значение угла.
Синтаксис всех прямых тригонометрических функций одинаков. Например, синтаксис функции SIN
SIN(А),
где
А - угол в радианах, для которого определяется синус.
Точно так же одинаков и синтаксис всех обратных тригонометрических функций. Например, синтаксис функции АSIN
АSIN(А),
где
А - число, равное синусу определяемого угла.
Следует обратить внимание, что все тригонометрические вычисления производятся для углов, измеряемых в радианах. Для перевода в более привычные градусы следует использовать функции преобразования (ГРАДУСЫ, РАДИАНЫ) или самостоятельно переводить значения, используя функцию ПИ().
Функция ПИ() вставляет значение числа 
(пи). Аргументов функция не имеет, но скобки после названия удалять нельзя.
Например, при необходимости рассчитать значение синуса угла, указанного в градусах, необходимо его умножить на ПИ()/180.
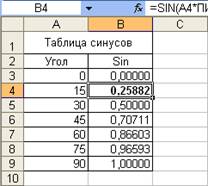
Рис.5. Вычисление тригонометрических функций для углов, указанных в градусах
Преобразование чисел
Преобразование чисел может потребоваться при переводе углов из градусов в радианы и обратно, при определении абсолютной величины числа, при преобразовании арабских цифр в римские.
Для перевода значения угла, указанного в радианах, в градусы используют функцию ГРАДУСЫ.
Синтаксис функции
ГРАДУСЫ(А),
где
А - угол в радианах, преобразуемый в градусы.
Для перевода значения угла, указанного в градусах, в радианы используют функцию РАДИАНЫ.
Синтаксис функции
РАДИАНЫ(А),
где
А - угол в градусах, преобразуемый в радианы.
Функции ГРАДУСЫ и РАДИАНЫ удобно использовать с тригонометрическими функциями. Например, при необходимости можно рассчитать значение синуса угла, указанного в градусах (рис. 6).
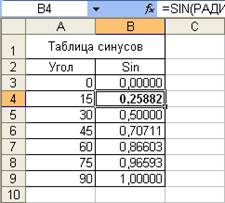
Рис. 6. Вычисление тригонометрических функций с использованием функций "ГРАДУСЫ" и "РАДИАНЫ"
Комбинаторика
Для расчета числа возможных комбинаций (групп) из заданного числа элементов используют функцию ЧИСЛКОМБ.
Синтаксис функции
ЧИСЛКОМБ(А; В),
где
А - число элементов;
В - число объектов в каждой комбинации.
Во вспомогательных расчетах в комбинаторике может потребоваться расчет факториала числа. Факториал числа - это произведение всех чисел от 1 до числа, для которого определяется факториал. Например, факториал числа 6 (6!) равен 1*2*3*4*5*6. Для расчета факториала используют функцию ФАКТР.
Синтаксис функции
ФАКТР(А),
где
А - число, для которого рассчитывается факториал.
Факториал нельзя рассчитать для отрицательных чисел. Факториал числа 0 (ноль) равен 1. При расчете факториала дробных чисел десятичные дроби отбрасываются.
Генератор случайных чисел
В некоторых случаях на листе необходимо иметь число, которое автоматически и независимо от пользователя может принимать различные случайные значения.
Для создания такого числа используют функцию СЛЧИС(). Функция вставляет число, большее или равное 0 и меньшее 1. Новое случайное число вставляется при каждом вычислении в книге. Аргументов функция не имеет, но скобки после названия удалять нельзя.
Статистические вычисления
Расчет средних значений
В самом простом случае для расчета среднего арифметического значения используют функцию СРЗНАЧ.
Синтаксис функции
СРЗНАЧ(А),
где
А - список от 1 до 30 элементов, среднее значение которых требуется найти. Элемент может быть ячейкой, диапазоном ячеек, числом или формулой. Ссылки на пустые ячейки, текстовые или логические значения игнорируются.