Относительная величина выполнения задания
Рассчитывается как отношение фактически достигнутого в данном периоде уровня к запланированному. Так, в 1988 г. было произведено стиральных машин 6103 тыс. шт. при плане (госзаказе) 6481 тыс. шт. Относительная величина выполнения плана составила
Iвып.пл. = 6103: 6481 = 0,942, или 94,2%.
Следовательно, плановое задание было невыполнено на 5,8%.
На практике различают две разновидности относительных показателей выполнения плана. В первом случае сравниваются фактические и плановые уровни (таков пример, рассмотренный выше). Во втором случае в плановом задании устанавливается абсолютная величина прироста или снижения показателя и собственно проверяется степень выполнения плана по этой величине. Так, если планировалось снизить себестоимость единицы продукции на 24,2 руб., а фактическое снижение составило 27,5 руб., то плановое задание по снижению себестоимости выполнено с ростом в 27,5: 24,2 = 1,136 раза, т.е. план перевыполнен на 13,6%. Показатель выполнения плана по уровню себестоимости в данном случае будет меньше единицы. Если фактическая себестоимость изделия равнялась 805,8 руб. при плановой 809,1 руб., то величина выполнения плана составила 805,8: 809,1 = 0,996, или 99,6%. Фактический уровень затрат на одно изделие оказался на 0,4% ниже планового.
В аналитических расчетах при исследовании взаимосвязей чаще применяется оценка выполнения плана по уровню показателя. Оценка выполнения плана по изменению уровня обычно приводится для целей иллюстрации, особенно если планируется снижения абсолютного значения затрат, расходов по видам и т.п.
Относительные величины динамики, планового задания и выполнения связаны соотношением
11. Степеннные средние. Основные формулы.
Средняя величина является обобщающей характеристикой совокупности однотипных явлений по изучаемому признаку. Средняя величина должна вычисляться с учетом экономического содержания определяемого показателя.
Все виды средних делятся на:
· степенные (аналитические, порядковые) средние (арифметическая, гармоническая, геометрическая, квадратическая);
· структурные (позиционные) средние (мода и медиана) – применяются для изучения структуры рядов распределения.
Средняя степенная (при различной величине k) определяется:
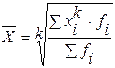
Виды средних степенных величин
| k | Наименование средней | Формула средней | Когда используется |
| Средняя арифметическая простая (невзвешенная) | 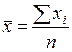 (1.2) где xi – i-й вариант осредняемого признака ( (1.2) где xi – i-й вариант осредняемого признака ( 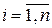 ); n – число вариант ); n – число вариант | Используется, когда расчет осуществляется по несгруппированным данным | |
| Средняя арифметическая взвешенная | 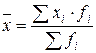 (1.3), где fi – частота повторяемости i-го варианта (1.3), где fi – частота повторяемости i-го варианта | Используется, когда данные представлены в виде рядов распределения или группировок | |
| -1 | Средняя гармоническая взвешенная | 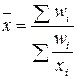 (1.4), где (1.4), где 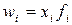 . . | Используется, когда известны индивидуальные значения признака и веса W за ряд временных интервалов |
| -1 | Средняя гармоническая невзвешенная | 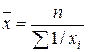 (1.5) (1.5) | Используется в случае, когда веса равны |
| Средняя геометрическая невзвешенная | 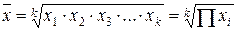 (1.6) (1.6) | Используется в анализе динамики для определения среднего темпа роста | |
| Средняя геометрическая взвешенная | 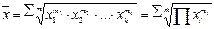 (1.7) (1.7) | ||
| Средняя квадратическая невзвешенная | 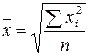 (1.8) (1.8) | Используется при расчете показателей вариации | |
| Средняя квадратическая взвешенная | 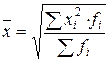 (1.9) (1.9) |
12. Средняя арифметическая, средняя гармоническая, средняя геометрическая.
Средняя арифметическая величина наиболее часто встречается в социально-экономических исследованиях. Средняя арифметическая применяется в форме простой средней и взвешенной средней.
Средняя арифметическая простая рассчитывается по несгруппированным данным на основании формулы
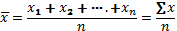
где x- индивидуальные значения признака (варианты);
n- число единиц совокупности.
Пример. Требуется найти среднюю выработку рабочего в бригаде, состоящей из 15 человек, если известно количество изделий, произведенных одним рабочим (шт.): 21; 20; 20; 19; 21; 19; 18; 22; 19; 20; 21; 20; 18; 19; 20.
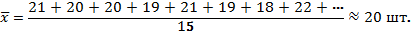
Средняя арифметическая простая рассчитывается по несгруппированным данным на основании формулы
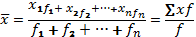
где f - частота повторения соответствующего значения признака (варианта);
∑f — общее число единиц совокупности (∑f = n).
Средняя гармоническая величинаявляется модификацией средней арифметической. Применяется в тех случаях, когда известны индивидуальные значения признака, т. е. варианты (x), и произведений вариант на частоту (xf=М), но неизвестны сами частоты (f).
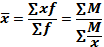
Пример. Требуется определить средний размер заработной платы работников объединения, состоящего из трех предприятий, если известен фонд заработной платы и средняя заработная плата работников по каждому предприятию.
| Предприятие | Фонд заработной платы, тыс. руб., xf | Средняя заработная плата, тыс. руб., x |
| 40 700 | ||
| 38 700 | ||
| 50 700 | ||
| ВСЕГО |
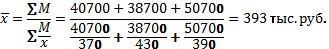
Средняя гармоническая простая в практике статистики используется крайне редко. В тех случаях, когда xf= Mm = const, средняя гармоническая взвешенная превращается в среднюю гармоническую простую
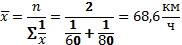
Средняя геометрическая величина используется при расчете средних показателей динамики. Средняя геометрическая применяется в форме простой средней (для несгруппированных данных) и взвешенной средней (для сгруппированных данных).
Средняя геометрическая простая
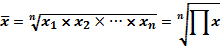
где n— число значений признака;
П — знак произведения.
