Основные позиции закона РФ «Об обеспечении единства измерений» от 26.06.2008 № 102 – ФЗ. 9 страница

Рисунок 16 – Экономические показатели качества

Себестоимость и цена единицы оцениваемой продукции характеризуют в основном ее технологичность и условия производства.

На себестоимость единицы продукции, выпускаемой с помощью оцениваемого изделия, влияют различные характеристики этого изделия.

Приведенные затраты на единицу продукции определяют по формуле

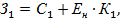
где С₁ – себестоимость единицы продукции;

Е_н – нормативный коэффициент экономической эффективности капитальных вложений, равный 0,15;

К₁ – удельные производственные фонды (среднегодовая сумма основных и оборотных средств), отнесенных к величине годового выпуска продукции. Этот показатель выполняет те же функции, но является более полным и точным.

Приведенные затраты на единицу продукции, выпускаемой с помощью оцениваемого изделия, представляют собой интегральный показатель качества, так как он может быть выражен как отношение эффекта к затратам.

Величина затрат определенного вида на единицу продукции, выпускаемой с помощью оцениваемого изделия, может быть использована в качестве экономического показателя, если прочие виды затрат незначительны или неизменны.

Относительный экономический показатель продукции определяется соотношением затрат на эксплуатацию или потребление базового образца и затрат на эксплуатацию или потребление оцениваемой продукции.

Возможно формирование и других показателей качества и их групп.

Выбор определяющих признаков для классификации продукции с целью оценки ее уровня качества – основная задача предприятия, стремящегося выйти на передовые позиции.

При классификации продукции следует указывать вид, группу и подгруппу, класс и подкласс в соответствии с общегосударственным классификатором продукции.

2.11 Шкалы измерений

2.11.1 Измерения являются инструментом познания объектов и явлений окружающего мира. Поэтому метрология относится к науке, занимающейся теорией познания – гносеологии.

Измерение – это алгоритмическая операция, которая данному наблюдаемому состоянию объекта, процесса, явления ставит в соответствие определенное обозначение: число, номер или символ.

Допустимые в дальнейшем способы обработки полученных данных сильно зависят от способа, которым они были измерены.

Одним из наиболее важных моментов в измерении является тип измерительной шкалы.

Шкала - это упорядоченный ряд отметок, соответствующий соотношению последовательных значений измеряемых величин.

В квалиметрии шкала измерений является средством адекватного сопоставления и определения численных значений отдельных свойств и качеств различных объектов.

Практически используют пять видов квалиметрических шкал: шкалу наименований, шкалу порядка, шкалу интервалов, шкалу отношений и шкалу абсолютных значений.

2.11.2 Шкала наименований. В тех случаях, когда несколько неизвестных размеров необходимо сопоставлять с одним и определить, какие из них равны размеру, вы-бранному за базу сравнения, а какие нет, тогда используют так называемую шкалу наименований.

По шкале наименований классифицируют размеры по признаку эквивалентности, тождества, равенства. Такое измерение размеров является наиболее простым и наименее информативным.

При этом не определяется, какой из неодинаковых размеров больше или меньше размера, принятого за базовый. Отношение порядка возрастания или уменьшения размеров не устанавливается.

Измерение заключается только в определении одинаковости (равенства) или отличия (неравенства) того или иного размера от заранее определенного значения.

Следовательно, определяющие отношения между измеряемыми размерами таковы: равны или не равны, т. е. в символах = или ≠.

Математическое выражение сущности измерений по шкале наименований можно записать так:

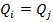или ,

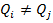где Q_j – размер, с которым сравнивают (базовый размер);

Q_i – i – й из сравниваемых размеров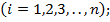

n – число сравниваемых размеров.

При сопоставлении и измерении размеров по шкале наименований осуществляется, например, контроль и оценка качества чего-либо по альтернативному принципу: годен - не годен; подходит - не подходит; соответствует - не соответствует и т. п.

Так осуществляют контроль калибрами деталей машин и иных изделий на предприятиях - изготовителях продукции, при входном контроле, а также в ряде других случаев. Контроль калибрами -это специальный тип измерений, выполняемый с целью установления отношения между измеряемыми размерами и известным размером калибра.

Над обозначениями на шкале наименований, даже если эти обозначения числовые, нельзя производить арифметические операции, а только операцию проверки их совпадения. С результатами операции проверки совпадения можно выполнять более сложные преобразования: считать количество совпадений, вычислять и сравнивать относительные частоты, выполнять статистические процедуры и др.

Пример. Рассмотрим шкалу цифр на дисковом телефоне. Какова она? Как видите, на практике бывает достаточно трудно понять, что некоторая шкала является шкалой наименований.

Дальнейшим развитием шкалы наименований является порядковая (ординальная, ранговая) шкала, которая позволяет некоторым образом сравнить классы, указать порядок следования квантификаторов.

2.11.3 Шкала порядка. Простейшим видом измерения (получения опытным путем представления о каком-либо размере) является экспериментальное сравнение его с другим размером той же меры по принципу «что больше (меньше)?» или «что лучше (хуже)?».

Например, масса m₁ одного из двух образцов одного и того же изделия (рисунок 17) может быть больше массы m₂ второго образца, но для решения вопроса о том, какой из них легче, получаемой таким образом измерительной информации вполне

достаточно. Если изделие предназначено для использования на летательных аппаратах, то качество второго образца по этому показателю выше, чем первого.

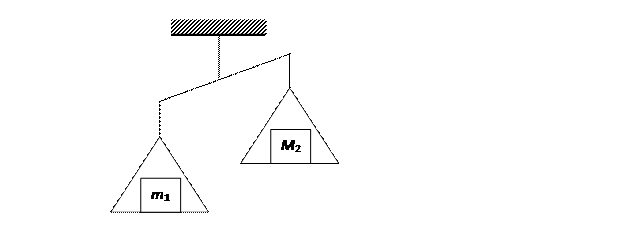
Рисунок 17 – Сравнение двух размеров однородной меры (массы) по шкале порядка

Подобным же образом можно визуально сравнить линейные размеры двух изделий (длину, ширину, высоту) и вынести суждение о том, качество какого из изделий выше по каждому из этих показателей транспортабельности.

Можно по прибору или на глаз сравнить освещенность рабочего места, создаваемую разными светильниками, сделать вывод о том, качество каких светильников выше по этому эргономическому показателю.

Число сравниваемых между собой размеров, как в последнем примере со светильниками, может быть достаточно большим. Расположенные в порядке возрастания или убывания, они образуют шкалу порядка.

Так, на многих конкурсах и соревнованиях мастерство исполнителей и спортсменов (или целых команд) определяется их местом, занятым в итоговой таблице. Последняя, таким образом, является шкалой порядка - формой представления измерительной информации, отражающей тот факт, что мастерство одних выше мастерства других, хотя и неизвестно, в какой степени (насколько или во сколько раз).

Построив людей по росту, можно, пользуясь шкалой порядка, сделать вывод о том, кто выше, однако сказать, насколько выше или во сколько раз нельзя.

Расстановка размеров в порядке их возрастания или убывания для получения измерительной информации по шкале порядка называется ранжированием.

При построении шкалы порядка (ранжированного ряда) широко используется способ попарного сопоставления, когда измеряемые размеры сначала сравниваются между собой попарно и для каждой пары результат сравнения выражается в форме «больше-меньше» или «лучше-хуже». Затем ранжирование производится на основании результатов попарного сопоставления.

Математическим выражением соотношений попарно сопоставляемых размеров является:

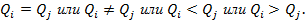
Классическим примером оценивания с применением шкалы порядка является оценивание твердости минералов на основе шкалы Мооса. Шкала Мооса относительной твердости минералов состоит из 10 эталонов твердости: тальк – 1, гипс – 2, кальцит – 3, флюорит -4, апатит – 5, ортоклаз – 6, кварц – 7, топаз – 8, корунд – 9, алмаз – 10.

Относительная твердость путем царапания эталоном шкалы Мооса по поверхности испытываемого объекта. Если эталон, имеющий твердость n (n = 1, 2, ..., 10), царапает исследуемый образец, а исследуемый образец царапает эталон с твердостью n – 1, то твердость минерала принимается равной (n – 1). В рассмотренном примере оценивание в шкале порядка обусловлено тем фактом, что для оценивания исследуемого свойства не существует метода, позволяющего осуществить оценку в установленных единицах измерения.

Особенно широкое распространение измерения по шкале порядка получили в духовной сфере, в области интеллектуального труда, искусстве, гуманитарных науках, где переход к точным количественным методам исследований только намечается.

По шкале порядка сравниваются между собой размеры, которые сами остаются неизвестными. Результатом сравнения является ранжированный ряд. В зависимости от того, как он получен, ранжированный ряд может быть:

- результатом измерений, если сравнение размеров производилось опытным путем;

- результатом вычислений, если сравнение размеров производилось теоретически (расчетным методом);

- смешанным ранжированным рядом, т. е. просто результатом сравнения размеров по шкале порядка, если сравнение производилось и теоретически, и экспериментально.

Отношение порядка ничего не говорит о дистанции между сравниваемыми классами. Порядковые экспериментальные данные, даже если они изображены цифрами, нельзя рассматривать как числа, над ними нельзя выполнять действия, которые приводят к получению разных результатов при преобразовании шкалы, не нарушающем порядка.

Например, нельзя считать среднее, делить значение на значение или коэффициент.

Измерения по шкале порядка являются самыми несовершенными, наименее информативными. Они не дают ответа на вопрос о том, насколько или во сколько раз один размер больше другого. На шкале порядка определены (т. е. могут выполняться) лишь некоторые логические операции. Например, если первый размер больше второго, а второй больше третьего, то и первый больше третьего: Q₁ > Q₂, а Q₂ > Q₃, то Q₁ > Q₃. Или если хоть один из двух размеров больше третьего, то их сумма тоже больше третьего. Если два размера меньше третьего, то их разность меньше третьего.

Эти свойства шкалы порядка называются свойствами транзитивности.

В то же время на шкале порядка не определены (т. е. не могут выполняться) никакие арифметические действия.

Интервалы между реперными точками неизвестны (на шкале не установлен масштаб), поэтому баллы нельзя складывать, вычитать, перемножать или делить.

В принципе их можно заменить любыми символами (буквами или знаками). Измерительная информация, полученная по шкале порядка, непригодна для математической

обработки (переработки). Невозможно и внесение в результат измерительного эксперимента поправки, ибо если ни сами сравниваемые размеры, ни разность между ними неизвестны, то останется неизвестным, изменится ли соотношение между ними после учета поправки.

Измерения по шкале порядка широко используются при контроле. Здесь проверяемый размер Q_i сравнивается с контрольным размером Q_j.

Результатом измерения служит решение о том, годно или нет изделие по контролируемому параметру.

Особое место занимает сравнение с размером, равным нулю. Оно называется обнаружением. Таково, например, обнаружение сигналов на фоне помех. Результатом обнаружения служит решение о том, есть сигнал или нет.

2.11.4 Шкала интервалов. На измерительной шкале интервалов фиксируются отличия сопоставляемых размеров.

Это форма отображения величин измеряемого является более совершенной, так как на шкале интервалов есть условные, но вполне определенные единицы измерений, что позволяет количественно (численно) охарактеризовать соотношение исследуемых размеров.

Математическая запись сравнения между собой двух однородных размеров по их разнице имеет вид

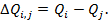(5)

На шкале интервалов определяют такие соотношения размеров, как: равно (=), не равно 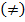, больше 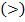, меньше 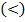, сумма (+), разность (-).

Следовательно, здесь определено отношение порядка и эквивалентности не только между размерами характеристик качества, но и между расстояниями между ними на шкале измерений.

Стремление получить возможность «оперировать с числами» приводит к дальнейшему усилению до интервальной шкалы, для которой известны расстояния между любыми квантификаторами (деления на шкале). Расстояния выражают в единицах, одинаковых по всей длине шкалы. Длина интервала не зависит от места его расположения на шкале.

Арифметические действия допустимы над длинами интервалов, но не над самими значениями квантификаторов, поскольку нуль в таких шкалах не единственен.

Некоторые величины по своей физической природе либо не имеют абсолютного нуля, либо допускают свободу выбора в установлении начала отсчета и поэтому измеряются в интервальных шкалах: температура, время, высота местности.

В статистике центральные моменты (в том числе и дисперсия) имеют объективный физический смысл, а начальные моменты (в том числе и среднее значение) являются относительными наряду с началом отсчета.

Градация – это установление масштаба по шкале интервалов. Масштаб, т.е. одна часть выбранного интервала между двумя базовыми (опорными, реперными) размерами, принимают за меру – за единицу измерений.

Классическим примером измерений по шкале интервалов с двумя реперными точками является измерение температур по шкале Цельсия. На температурной шкале Цельсия (рисунок 18) за начало отсчета принята температура таяния льда.

С ней сравниваются все другие температуры.

Для удобства пользования шкалой интервал между температурой таяния льда и температурой кипения воды разбит на 100 равных интервалов – градаций или градусов. Вся шкала Цельсия разбита на градусы как в сторону положительных, так и отрицательных интервалов.

На температурной шкале Реомюра за начало отсчета интервалов та же температура таяния льда, но интервал между этой температурой и температурой кипения воды разбитна 80 равных частей. Тем самым используется другая градация градация интервалов температуры: градус Реомюра больше градуса Цельсия.

Рисунок 18 – Температурные шкалы Цельсия (ºС), Реомюра (ºR), Фаренгейта (ºF) и Кельвина (К)

На температурной шкале Фаренгейта тот же интервал разбит на 180 градусов, следовательно, градус Фаренгейта меньше градуса Цельсия. Кроме того, начало отсчета интервалов на шкале Фаренгейта сдвинуто на 32º в сторону низких температур.

Деление шкалы интервалов на равные части – градации - устанавливает на ней масштаб и позволяет выразить результат измерения в числовой мере.

При наличии масштаба измерение по шкале интервалов сводится к подсчету числу градаций, укладывающихся в интервале 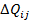. Градация таким образом выступает в качестве единицы измерения.

Ввиду неопределенности начала отсчетамультипликативные операции (умножение и деление) на шкале интервалов не определены. Соответственно, по шкале интервалов нельзя определить, во сколько раз один размер больше или меньше другого.

Особым случаем является сравнение 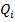с 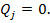В отличие измерений на шкале

порядка, где подлобное сравнение производится сравнение с целью обнаружения 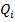, на шкале интервалов такое сравнение позволяет измерить 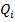, так как измерение интервала 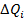при 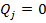тождественно измерению самого размера .

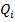Примером шкалы интервалов, построенной при 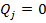(она в этом случае называется шкалой отношений), может служить температурная шкала Кельвина, приведенная на рисунке 18. На ней за начало отсчета принят абсолютный нуль температуры, при котором прекращается тепловое движение молекул. Более низкой температуры быть не может. Второй реперной точкой служит температура тройной точки воды. По шкале Цельсия интервал между этими реперами равен 273,16 ºС. Поэтому на шкале Кельвина он разделен на равные части, равные 1/273,16 интервала. Каждая такая часть называется Кельвином и равна градусу Цельсия, что значительно облегчает переход с одной шкалы к другой.

2.11.5 Шкала отношений

Для того, чтобы определить не только на сколько, но во сколько один размер больше или меньше другого, или количественно измерить величину размера в официально установленных единицах измерения, необходимо воспользоваться шкалой отношений.

Примерами величин, природа которых соответствует шкале отношений, являются длина, масса, деньги.

Шкала отношений - это измерительная шкала, на которой отсчитывается (определяется) численное значение величины q как математического отношения измеряемого размера Q к другому известному размеру, принимаемому за единицу измерения .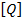

В метрологии и квалиметрии считается, что любое измерение по шкале отношений предполагает сравнение неизвестного размера с известным и выражением первого через второй в кратном или дольном отношении.

Математическая запись измерения по шкале отношений имеет вид

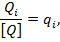
где 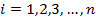- номер измеряемого размера.

Шкала отношений – это шкала интервалов, в которой определен нулевой элемент – начало отсчета, а также размер (масштаб) единицы измерения.

По шкале отношений определяются такие значения измеряемых размеров, как: равно (=), не равно (≠), больше (>), меньше (<), сумма (+), разница размеров (-), умножение (∙), деление (:), т.е. можно производить все арифметические действия со значениями величин.

Шкала отношений наиболее приемлема для измерений большинства показателей качества, особенно для таких численных характеристик, как геометрические размеры объектов, их плотность, сила, напряжение, частота колебаний и прочие.

2.11.6 Абсолютная шкала

Последней и самой «сильной» является абсолютная шкала. Она имеет абсолютный нуль и абсолютную единицу. Является единственной и уникальной. Важной особенностью абсолютной шкалы по сравнению со всеми остальными является отвлеченность (безразмерность) и абсолютность ее единицы.

Указанная особенность позволяет производить над показаниями абсолютной шкалы такие операции, которые недопустимы для других шкал, употреблять эти показания в качестве показателя степени и аргумента логарифма (подобная необходимость часто возникает, например, при обработке психологических экспериментов).

Во многих случаях напрямую измеряется величина чего-либо. Например, непо-

средственно подсчитывается число дефектов в изделии, количество единиц произведенной продукции, сколько студентов присутствует на лекции, количество прожитых лет и т. д. При таких измерениях на измерительной шкале отмечаются абсолютные количественные значения измеряемого.

Такая шкала абсолютных значений обладает теми же свойствами, что и шкала отношений, с той лишь разницей, что величины, обозначенные на этой шкале, имеют абсолютные, а не относительные значения.

Результаты измерений по шкале абсолютных величин имеют наибольшую достоверность, информативность и чувствительность к неточностям измерений.

Шкалы интервалов, отношений и абсолютных величин называются метрическими, так как при их построении используются некоторые меры, т. е. размеры, принятые в качестве единиц измерений.

2.11.7 Шкалы на основе «предпочтительных чисел»

Измерительные шкалы, основанные на использовании рядов предпочтительных чисел, обычно являются метрическими шкалами интервалов или абсолютных величин, исчисляемых, например, единицами допусков измеряемых линейных размеров или квалитетами.

Предпочтительными называют числа, наиболее часто используемые в технике, в технологии, в науке и в других сферах деятельности людей.

Они представляют собой определенное множество взаимосвязанных чисел (ряд чисел), которые обладают систематизирующим свойством, что позволяет использовать их при выборе, назначении и измерении размеров различных величин.

Такие математические ряды чисел формально характеризуют различные зависимости и закономерности изменений в реальном мире.

Чаще всего математические выражения изменяющихся состояний имеют вид простой арифметической (линейной) или геометрической (нелинейной) прогрессии.

Ряды чисел арифметической прогрессии имеют постоянную разницу между двумя соседними числами.

Ряд чисел геометрической прогрессии отличаются тем, что произведение или частное любых двух чисел ряда всегда является членом этого ряда.

Геометрическая прогрессия - это ряд последовательно возрастающих или убывающих чисел с постоянным отношением между двумя соседними числами. Это отношение называется знаменателем прогрессии φ. Следовательно, каждый член геометрической прогрессии является произведением предыдущего члена на знаменатель φ.

Любой член ряда N_i геометрической прогрессии находится по формуле

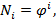
где φ – знаменатель прогрессии;

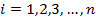- номер элемента ряда.

В связи с перечисленными свойствами геометрической прогрессии зависимости, определяемые из произведений членов или их целых степеней, всегда подчиняются закономерности этого ряда. Например, если ряд будет определять линейные размеры, то площади или объемы, образованные из этих линейных размеров, также подчиняются его закономерности.

Так как везде принята десятичная система счета чисел, начиная с единицы, то наболее удобным являются геометрические прогрессии, включающие число 1 и имеющие 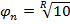с n, кратным 10.

Международная организация по стандартизации ИСО установила (рекомендация Р ИСО 497) четыре основных десятичных ряда предпочтительных чисел с такими знаменателями

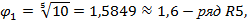
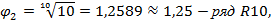
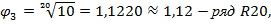
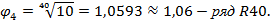
В отдельных обоснованных случаях допускается применение рядов

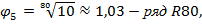
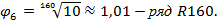
Следует отметить, что установленные ИСО ряды предпочтительных чисел основаны не только на десятичной системе счета, но и на принципе оптимальных соотношений, который реализован, например, в золотом сечении. Под золотым сечением понимают прямоугольник со сторонами a и b, которые соотносятся между собой как

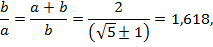
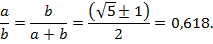
Золотое сечение считается эстетически идеальной пропорцией, общим природным законом. Человеческое тело построено в пропорциях золотого сечения, также и более низшие живые организмы и даже растения показывают те же пропорции. И все это не находит обоснования посредством реальных физических законов.

Существуют и иные геометрические прогрессии для образования рядов предпочтительных чисел.

Предпочтительные числа геометрических прогрессий используются, в частности, в квалиметрии для установления величин коэффициентов весомости (значимости) отдельных показателей качества, при градации мер, при делении диапазона оценивания на шкалы (формирование шкал измерения) и т.д.

На практике используются не только ряды R. Так, например, в радиотехнике часто применяют предпочтительные числа рядов Е, установленных Международной электротехнической комиссией МЭК

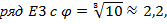
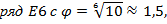
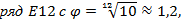
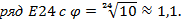
2.12 Понятие штрихового кодирования

Штриховой код (ШК)состоит из чередующихся темных (штрихов) и светлых (пробелов) полос разной ширины. Размеры полос стандартизованы.

Штриховые коды предназначены для считывания сканерами, которые декодируют штрихи в цифры через микропроцессоры и вводят инфор­мацию о товаре в компьютер.

Штриховое кодирование способствует повышению конкурентоспособности товара, увеличивает спрос на него, так как потребитель уверен в том, что это не фальсификат.

В ряде стран без штрихового кода продукция не принимается к реализации. Он повышает престиж товара, играет роль рекламы, улучшает культуру обслуживания.

Каждая единица товара идентифицируется с помощью штрихового и цифрового кода.

Кроме того, штриховой код способствует организации эффективного контроля за товародвижением, начиная с предприятия-изготовителя и до склада магазина.

Он применяется также для учета и контроля товаров в пределах предприятия (сокращение складских площадей, уменьшение потерь на банальное воровство, отслеживание наличия товара на складе, отсутствие просроченного товара, мобильное управление ценой, возможность иметь на складе только оперативный запас, полноценный электронный (безбумажный) учет).

Полный штриховой код позволяет закупочным торговым или внеш­неторговым организациям иметь четкие реквизиты происхождения то­вара и адресно предъявлять претензии по качеству, безопасности и дру­гим параметрам, не соответствующим контракту (договору).

Наличие штрихового кода является обязательным условием экспорта товаров.

По номеру на упаковке через национальную организацию товарной нумерации можно отыскать продукцию данного предприятия, определить изготовителя товара. Информация о кодах предприятий хранится в банке данных национальной организации.

Существует заблуждение, что по первым цифрам ШК можно определить страну