Родственные статистические функции

Функция СТАНДОТКЛОН

СТАНДОТКЛОН (число1; число2;...)

Результат;

Оценивает генеральное стандартное отклонение по выборке.

Аргументы;

Число 1, число2,….. - аргументы, соответствующие выборке из генеральной совокупности.

Замечания;

· Функция СТАНДОТКЛОН предполагает, что аргументы являются выборкой из генеральной совокупности. Если данные представляют всю генеральную совокупность, то стандартное отклонение следует вычислять с помощью функции СТАНДОТКЛОНП;

· логические значения, такие, как ИСТИНА или ЛОЖЬ, а также текст игнорируются. Если текстовые и логические значения игнорироваться не должны, следует использовать функцию СТАНДОТКЛОНА.

Математико-статистическая интерпретация;

Внимание! Функция СТАНДОТКЛОН рассчитывает генеральное стандартное отклонение при условии, что исходные данные образуют выборочную совокупность. Если совокупность является генеральной, необходимо воспользоваться функцией СТАНДОТКЛОНП.

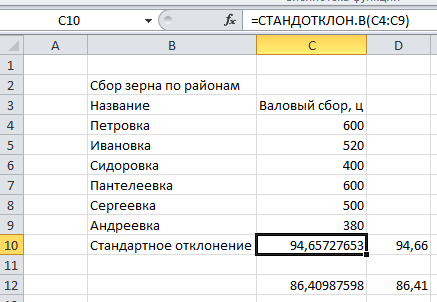
Используя выборочные данные, приведенные в табл. 4.10, по формуле =СТАНДОТКЛОН(С4:С9) получим стандартное отклонение 94,66 (сравните со значением 86,41, вычисляемым функцией СТАНДОТКЛОНП).

Табл.4.10.

В режиме «Описательная статистика» функция СТАНДОТКЛОН совместно с функцией СЧЕТ используется также для определения средней ошибки выборки 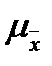- (показатель Стандартная ошибка в табл.4.2, (смотри предыдущий первый файл) «Описательная статистика»).

Средняя ошибка выборки характеризует стандартное отклонение вариантов выборочной средней от генеральной средней и зависит от колеблемости признака в генеральной совокупности, числа отобранных единиц и, а также, от способа организации выборки. Средняя ошибка повторной собственно-случайной выборки определяется по формуле

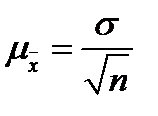
где σ — оценка генерального стандартного отклонения;

n — объем выборочной совокупности.

Средняя ошибка выборки 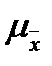используется для расчета предельной ошибки выборки Δ_х (показатель Уровень надежности в табл. 4.2), которая дает возможность выяснить, в каких пределах находится величина генеральной средней.

В математической статистике установлено, что предельная ошибка выборки Δ_х связана со средней ошибкой выборки 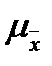соотношением

Δ_х = t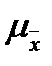

где t — коэффициент доверия (определяется в зависимости от того, с какой доверительной вероятностью нужно гарантировать результаты выборочного обследования).

В Microsoft Excel коэффициент доверия t рассчитывается через функцию СТЬЮДРАСПОБР, в которой в качестве аргументов задаются уровень значимости α и число степеней свободы k.

Уровень значимости α связан с доверительной вероятностью γ (задается в поле Уровень надежности диалогового окна Описательная статистика, рис. 4.1) выражением α = 1 — γ.

Число степеней свободы k зависит от объема выборки n и связано с ним выражением k =n - 1.

Внимание! В раздел статистических функций Microsoft Excel для вычисления значения предельной ошибки выборки включена также и функция ДОВЕРИТ. Данную функцию можно использовать при сравнительно большом числе единиц выборочной совокупности (n > 100), когда расхождение между средней выборки и генеральной средней становится практически несущественным (распределение Стьюдента приближается к нормальному распределению). Для малых выборок это расхождение может быть весьма существенным, поэтому для расчета предельной ошибки выборки в этом случае необходимо пользоваться не нормальным распределением (функцией ДОВЕРИТ), а распределением Стьюдента (функцией СТЬЮДРАСПОБР).

Функция ДИСП

Синтаксис:

ДИСП (число1; число2;...)

Результат

Оценивает генеральную дисперсию по выборке.

Аргументы;

Число 1,число2, ………, - аргументы, соответствующие выборке из генеральной совокупности.

Используя выборочные данные, приведенные в табл. 4.10, по формуле =ДИСП(С4:С9) получим оценку генеральной дисперсии - 8960.

Функция ЭКСЦЕСС

Синтаксис;

ЭКСЦЕСС (число1; число2;...)

Результат:

Оценивает эксцесс по выборке.

Число1, число2, ...... - аргументы, для которых вычисляется эксцесс.

Математико-статистическая интерпретация;

Эксцесс характеризует так называемую «крутость», т. е. островершинность или плосковершинность распределения. Он может быть рассчитан для любых распределений, но в большинстве случаев вычисляется только для симметричных. Это объясняется тем, что за исходную принята кривая нормального распределения, для которой E_k= 0. Относительно этой вершины и определяется выпад вверх или вниз вершины эмпирического распределения. Функция ЭКСЦЕСС рассчитывает значение эксцесса как для симметричных, так и для асимметричных распределений.

Наиболее точным и распространенным является определение эксцесса, основанное на расчете центрального момента 4-го порядка:

E_k =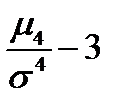

Применение данной формулы дает возможность вычислить значение эксцесса в генеральной совокупности.

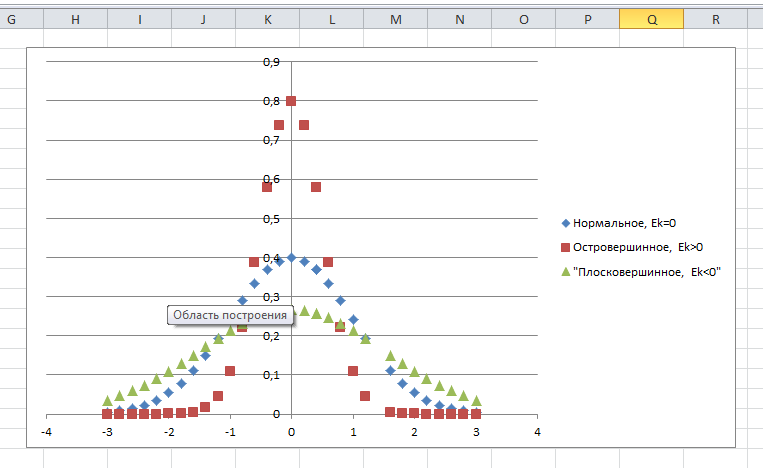
Рис.4.3

При этом если E_k > 0, распределение островершинное (рис. 4.3), если E_k < 0 — плосковершинное (рис. 4.3).

Еk=0

Еk<0

Еk>0

Рис 4.3

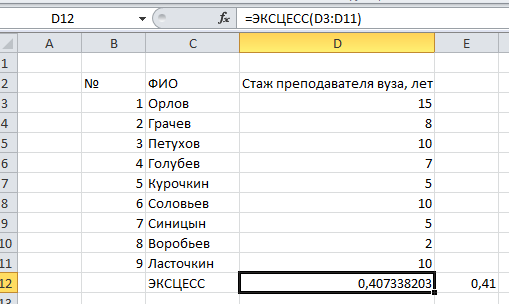
Рассмотрим расчет эксцесса по выборочным данным, представленным в табл. 4.11.

Таблица 4.11

Если данные образуют не выборочную, а генеральную совокупность, то эксцесс необходимо рассчитывать по стандартной формуле через центральный момент 4-го порядка и стандартное отклонение (табл. 4.12).

Табл.4.12

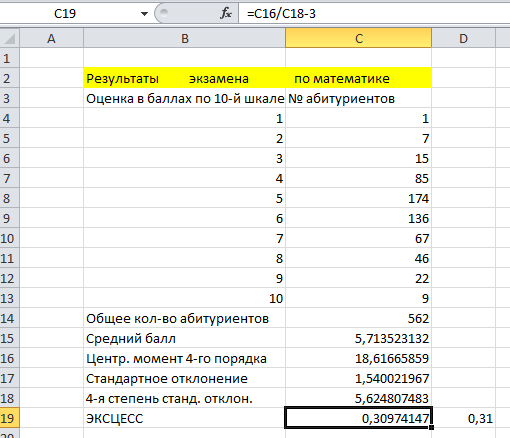
Содержимое ячеек в табл. 4.12:

ячейка С14 содержит формулу =СУММ(С4:С13) — рассчитывается общее количество абитуриентов;

ячейка С15 содержит формулу =СУММПРОИЗВ(В4:В13;С4:С13)/С14 - определяется средний балл сдачи экзаменов;

ячейка С16 содержит формулу =СУММПРОИЗВ(СТЕПЕНЬ(В4:В13-С15;4);С4:С13)/С14} — вычисляется центральный момент 4-го порядка;

ячейка С17 содержит формулу =КОРЕНЬ(СУММПРОИЗВ(СТЕПЕНЬ(В4:В13-С15;2);С4:С13)/С14)} - рассчитывается стандартное отклонение;

ячейка С18 содержит формулу = СТЕПЕНЬ(C17;4) – вычисляется 4-я степень стандартного отклонения;

ячейка С19 содержит формулу = С16/С18-3 – рассчитывается эксцесс.

В табл.4.11 и 4.12 эмпирические распределения имеют положительный эксцесс, т.е. они характеризуются скопление членов ряда в центрах распределений.

Функция СКОС

Синтаксис;

СКОС (число1; число2;...)

Результат;

Оценивает коэффициент асимметрии по выборке.

Аргументы:

Число1, число2………… - аргументы, для которых вычисляется коэффициент асимметрии.

Математико-статистическая интерпретация;

Определение формы кривой является важной задачей, так как статистический материал в обычных условиях дает по определенному признаку характерную, типичную для него кривую распределения. Всякое искажение формы кривой означает нарушение или изменение нормальных условий возникновения статистического материала.

Выяснение общего характера распределения предполагает оценку степени его однородности, а также вычисление показателей асимметрии и эксцесса.

Симметричным является распределение, в котором частоты любых двух вариантов, равноотстоящих в обе стороны от центра распределения, равны между собой.

Для симметричных распределений средняя арифметическая, мода и медиана равны между собой. С учетом этого показатель асимметрии основан на соотношении показателей центра распределения: чем больше разница между 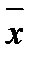, Мо, Ме, тем больше асимметрия ряда. При этом если Мо < Ме, асимметрия правосторонняя, если Мо > Ме - асимметрия левосторонняя.

Наиболее точным и часто используемым является показатель, основанный на определении центрального момента 3-го порядка (в симметричном распределении его значение равно нулю):

А_s =

Применение данного показателя дает возможность определить величину асимметрии в генеральной совокупности. При этом если А_s.> 0 — асимметрия правосторонняя (положительная), если А_s < 0 — асимметрия левосторонняя (отрицательная) (рис. 4.4).

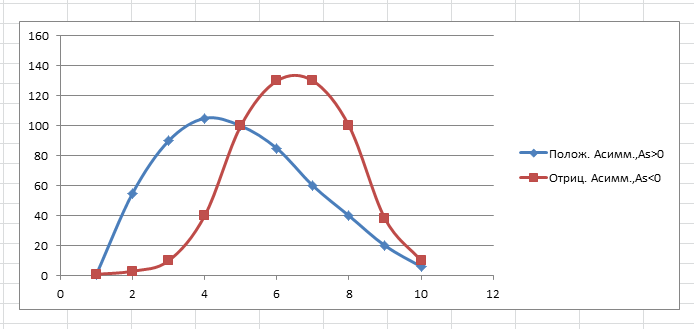
Рис.4.4

Симметричное As=0

ПравосторонняяAs>0

Левосторонняя As<0

Рис. 4.4.

Необходимо отметить, что функция СКОС определяет величину асимметрии по выборочной совокупности, поэтому в ней реализована формула

А_s =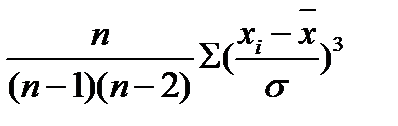

где n — объем выборки.

Рассмотрим расчет коэффициента асимметрии по выборочным данным, представленным в табл. 4.14.

Табл.4.14

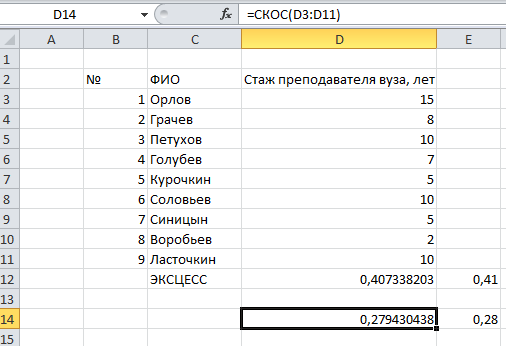
Ячейка D14 содержит формулу = CKOC(D3:D11).

Если данные образуют не выборочную, а генеральную совокупность, то асимметрию необходимо рассчитывать по стандартной формуле через центральный момент 3-го порядка и стандартное отклонение (табл. 4.15).

Табл.4.15

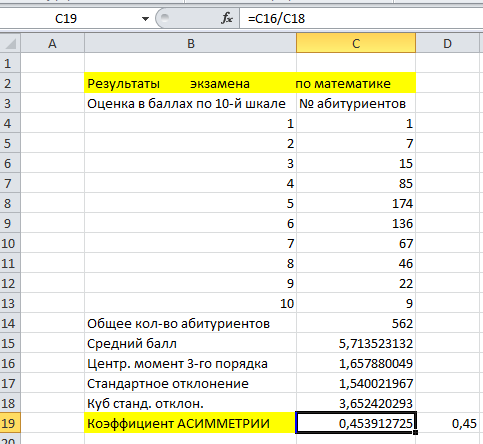
Содержимое ячеек в табл. 4.15:

ячейка С14 содержит формулу =СУММ(С4:С13) - вычисляется общее количество абитуриентов;

ячейка С15 содержит формулу =СУММПРОИЗВ(В4:В13;С4:С13)/С14 — определяется средний балл сдачи экзаменов;

ячейка С16 содержит формулу =СУММПРОИЗВ(СТЕПЕНЬ(В4:В13-С15;3);С4:С13)/С14 - рассчитывается центральный момент 3-го порядка;

ячейка С17 содержит формулу =КОРЕНЬ(СУММПРОИЗВ (СТЕПЕНЬ(В4:В13-С15;2);С4:С13)/С14) — вычисляется стандартное отклонение;

ячейка С18 содержит формулу =СТЕПЕНЬ(С17;3) — рассчитывается 3-я степень стандартного отклонения;

ячейка С19 содержит формулу =С16/С18 — рассчитывается коэффициент асимметрии.

В табл. 4.14 и 4.15 эмпирические распределения имеют положительную (правостороннюю) асимметрию, т. е. они характеризуются пологим склоном («хвостом») в правой части распределения.

Функция МИН

Синтаксис;

МИН (число1; число2;...)

Результат;

Находит наименьшее значение (х _min) в множестве данных.

Число1, число2,………. - аргументы, среди которых ищется минимальное значение.

Функция МАКС

Синтаксис;

МАКС (число 1; число2;...)

Результат

Находит наибольшее значение (x _max) в множестве данных.

В режиме «Описательная статистика» функции МАКС и МИН используются также для определения размаха вариации R (показатель Интервал в табл. 4.2).

Размах вариации показывает; насколько велико различие между единицами совокупности, имеющими наибольшее и наименьшее значение признака (например, различие между максимальной и минимальной пенсией различных групп населения, нормами выработки у рабочих определенной специальности или квалификации и т.п). Размах вариации рассчитывают как разность между наибольшим и наименьшим значениями варьирующего признака, т. е.

R= x _max - х _min

Функция СЧЕТ

Синтаксис;

СЧЕТ (значение1; значение2;...)

Результат;

Рассчитывает количество чисел в списке аргументов.

Значение1, значение2,........ - аргументы, которые могут содержать данные различных типов или ссылаться на них; в подсчете участвуют только числа.

Функция НАИБОЛЬШИЙ

Синтаксис;

НАИБОЛЬШИЙ (массив; k)

Результат;

Находит k-е по порядку (начиная с x _max ) наибольшее значение в множестве данных.

Аргументы:

массив, массив данных, для которых определяется k-е наибольшее значение;

k: позиция (начиная с наибольшей) в массиве ячеек данных.

Математико-статистическая интерпретация;

Функцию НАИБОЛЬШИЙ удобно применять при выборе значения по его относительному местоположению. Например, ее можно использовать, чтобы определить наилучший, второй, третий и т. д. результат в баллах, показанный при тестировании, измерении и т. п.

Если n — число точек в массиве данных, то функция НАИБОЛЬШИЙ(массив;1) находит наибольшее значение, а функция НАИБОЛЬШИЙ(массив;n) — наименьшее.

Функция НАИМЕНЬШИЙ

Синтаксис;

НАИМЕНЬШИЙ (массив; k)

Результат;

Находит k-е по порядку (начиная с х _min) наименьшее значение в множестве данных.

Математико-статистическая интерпретация;

Функцию НАИМЕНЬШИЙ удобно применять при выборе значения по его относительному местоположению. Например, ее можно использовать, чтобы определить наихудший, предпоследний и т. д. результат в баллах, показанный при тестировании, измерении и т. п.

Если n — число точек в массиве данных, то функция НАИМЕНЬШИЙ(массив;1) находит наименьшее значение, а функция НАИМЕНЬШИЙ(массив;n) — наибольшее.

Функция СТЬЮДРАСПОБР

В примере 4.1 функция СТЬЮДРАСПОБР используется для нахождения коэффициента доверия t (t-критерия Стьюдента) при расчете предельной ошибки выборки Δ_х (показатель Уровень надежности в табл. 4.2). Значение коэффициента доверия t рассчитывается по формуле =СТЬЮДРАСПОБР(0,05;В28-1),

где 0,05 - уровень значимости α = 1 - 0,95 (0,95 - доверительная вероятность, заданная в поле Уровень надежности диалогового окна «Описательная статистика», см. рис. 4.2);

В28-1 — число степеней свободы k = n - 1 = 9 - 1 = 8(в ячейке В28 - значение объема выборки n, рассчитываемое по формуле =СЧЕТ(В2:В10)).

Родственные статистические функции