Решение задачи методом зеркальных изображений

При одной бесконечной плоской границе, разделяющей два однородных и изотропных полупространства со средами, имеющими r1 и r2, потенциал электрического поля в каждой среде можно определить методом зеркальных изображений, исходя из следующих положений.

Условия непрерывности электрического поля и граничные условия

1.

2.При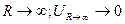

3. На границе раздела потенциалы в разных средах равны 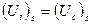(А).

4. должно соблюдаться постоянство нормальной составляющей 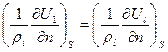(В).

Будут выполнены, если предположить следующее:

1. В среде 1, в которой находится источник тока, потенциал электрического поля будет таким, как в случае однородного безграничного пространства, заполненного средой с сопротивлением, равным сопротивлению полупространства, в котором находится источник тока, при условии, что кроме этого источника тока, в точке А¢, являющейся зеркальным изображением точки А в плоскости Р раздела сред, находится второй фиктивный источник тока А¢, отдающий некоторый ток I¢.

2. В среде 2, в которой источник тока А отсутствует, потенциал электрического поля будет таким, как будто все исследуемое пространство безгранично и заполнено этой средой, но источник А при этом отдает фиктивный электрический ток I¢¢.

Обозначая через R и R¢ расстояние от источников А и А¢ до точки М1 и М2 определим потенциал электрического поля.

для среды 1 (точка М1)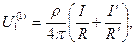

для среды 2 (точка М2)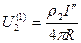

(индекс вверху – среда, где находится питающий электрод,

внизу – среда, где измеряется поле измерительным электродом).

Для определения фиктивных токов I¢ и I¢¢ воспользуемся пограничными условиями А и Б приравняв обе части при R=R¢ запишем:

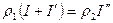[1]

и взяв производные (Б) получим:

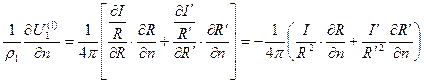и

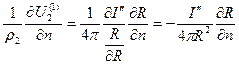
Так как 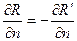, получим I-I¢=I¢¢ [2] R=R¢

Решая совместно [1] и [2] получим:

,

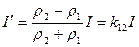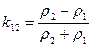
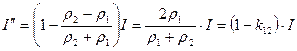
k12 – наз. коэффициент отражения

(1 – k12) – коэффициент пропускания.

В частности, если r2= ¥ k12= 1 и 1-k12= 0. В этом случае весь ток будет отражаться границей раздела (средой 2), в среде 2 токовое поле будет отсутствовать и в среде 1 плотность тока будет в 2 раза выше, чем в случае однородного изотропного пространства.

При идеально проводящей среде 2 (r2=0) k12= -1 1-k12= 2. В этом случае токовые линии не только не будут отражаться границей раздела, а, наоборот, будут полностью втягиваться средой 2. При этом весь ток, вместо того, чтобы растекаться по телесному углу 4p будет протекать в среду 2 и распространяться в телесном угле, равном 2p, что будет эквивалентным отдаче источником А фиктивного тока удвоенной силы.

Подставляя найденные значения I¢ и I¢¢, получим в среде1

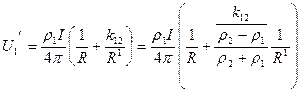
в среде 2

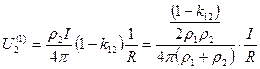
(В.Н. Дахнов, промысловая геофизика, Госоптехиздат, М, 1959 г.).