Задачи для самостоятельной проработки
(Циклические алгоритмы)
Задача 1
Найти и распечатать все натуральные трехзначные числа, равные сумме кубов своих цифр.
Задача 2
Вычислить значения функции
для значений аргумента x от -0.4 до 1.3 с шагом 0.1.
Задача 3
Даны натуральные числа n и k. Определить k-ю справа цифру числа n. Для поиска k-ой цифры использовать цикл.
Задача 4
По заданному вещественному x вычислить значение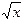 
по следующей итерационной формуле:
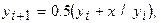
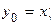
Итерации прекратить при
.
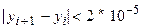Задача 5
Дано натуральное число n. Вычислить сумму k старших (находящихся слева) цифр числа.
Задача 6
Дано положительное число a. Найти k-ое число Фибоначчи, такое, что
.
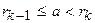Числа Фибоначчи: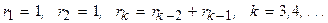 
.
Задача 7
Найти количество трехзначных чисел, кратных 15, но не кратных 30. Распечатать эти числа.
- Вывод в столбик
- Вывод матрицей
Задача 8
Вычислить, не используя функцию pow(), значения функции
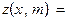
для значений аргументов:
x от -1.1 до 0.3 с шагом 0.2;
m от 1 до 5 с шагом 1.
Задача 9
По введенному целому числу M распечатать все трехзначные десятичные числа, сумма цифр которых равна M. Подсчитать также количество таких чисел или сообщить о том, что их нет.
Задача 10
Дано натуральное число N. Определить третью справа его цифру.
Задача 11
Вычислить значения функции
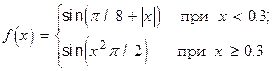
для значений аргумента
x от -0.5 до 1.2 с шагом 0.1.
Задача 12
Напечатать таблицу истинности логической функции
,
где &, Ú, - - знаки логических операций И, ИЛИ, НЕ.
Задача 13
По введенному натуральному числу N определить, является ли оно совершенным. Совершенное число равно сумме всех своих делителей, включая единицу и не включая себя.
Например: 6=1+2+3 - совершенное число; 8=1+2+4 - несовершенное.
Задача 14
Вычислить сумму членов бесконечного ряда
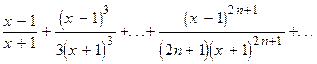
c точностью до члена ряда, меньшего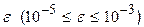 
.
Задача 15
Распечатать все четырехзначные натуральные десятичные числа из диапазона [2000..3000], в записи которых нет двух одинаковых цифр. Подсчитать количество таких чисел.
Задача 16
По заданному вещественному x вычислить значение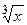 
по следующей итерационной формуле:
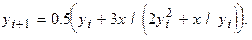
Начальное приближение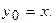 
Итерации прекратить при 
.
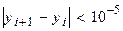Задача 17
Выяснить, какие цифры (по одной справа и слева) надо приписать к числу 1022, чтобы полученное число делилось на 7, 8, 9.
Задача 18
По заданному вещественному x (x<3) вычислить значение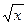 
по формуле двойной итерации:
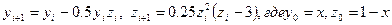
Итерации прекратить при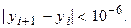 
Задача 19
Натуральное число m представить в виде суммы квадратов двух натуральных чисел. Выдать сообщение, если такое представление невозможно.
Задача 20
Найти наибольший общий делитель (НОД) двух введенных натуральных чисел, используя алгоритм Евклида.
Алгоритм Евклида: вычитаем из большего числа меньшее до тех пор, пока они не сравняются; полученное в результате число и есть НОД.
Задача 21
Даны вещественные числа А и В (A<B). Найти первый член последовательности
,
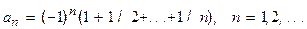который не принадлежит [A,B].
Задача 22
Даны вещественные числа A<0 и B>0. Найти первый член последовательности
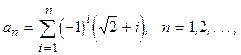
который не принадлежит отрезку [A, B].
Задача 23
Дано натуральное число N. Вычислить
.
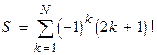Задача 24
В выражении (((( 1 ? 2) ? 3) ? 4) ? 5) ? 6 вместо каждого знака ? поставить знак одной из операций +, -, *, / так, чтобы результат вычислений был равен 35.