Решение контрольной работы №1
"Истинность высказываний. Тавтологии. Эквивалентности. Законы логики. Тождественные преобразования".
Вариант №1.
- Докажите эквивалентность:
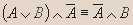
Решение.
| A | B | 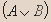 | 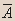 | 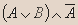 | 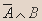 |
Вывод. Из таблицы видно, что
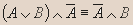
- Докажите, является ли данное высказывание тавтологией:
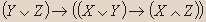
Решение.
| X | Y | Z | 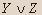 | 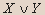 | 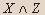 | 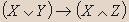 |  |
Вывод.Из таблицы видно, что высказывание не является тавтологией.- Установите истинность высказывания:
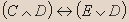
Решение.
| C | D | E | 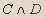 | 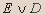 | 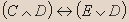 |
| 0 | 0 | 0 | |||
| 1 | 0 | 0 | |||
| 1 | 1 | 0 | |||
| 1 | 1 | 1 |
Вывод.Из таблицы видно, что высказывание истинно если:- C
 0; D
0; D  0; E
0; E  0;
0; - C
 1; D
1; D  0; E
0; E  0;
0; - C
 1; D
1; D  1; E
1; E  0;
0; - C
 1; D
1; D  1; E
1; E  1;
1; - Для формулы придумайте формализуемое ею высказывание:
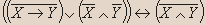
Решение.
Пусть:
X— «Сегодня чудесный день»
Y— “8 класс пишет контрольную работу”
Тогда и только тогда неверно, что, если сегодня чудесный день, то 8 класс пишет контрольную работу, или сегодня не чудесный день, и 8 класс не пишет контрольную работу, когда неверно, что сегодня чудесный день, и 8 класс пишет контрольную работу. - Данное высказывание преобразуйте в эквивалентное, но уже не содержащее отрицаний сложных высказываний:
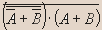
Решение.
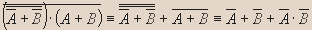
- Упростите:
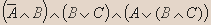
Решение.
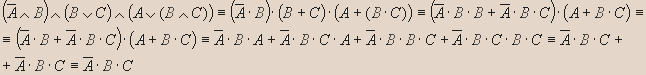
Вариант №2.
- Докажите эквивалентность:
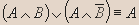
Решение.
| A | B | 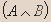 | 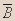 |  | 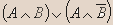 |
Вывод. Из таблицы видно, что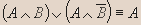
- Докажите, является ли данное высказывание тавтологией:
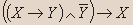
Решение.
| X | Y | 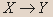 | 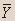 | 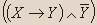 | 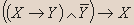 |
Вывод.Из таблицы видно, что высказывание не является тавтологией.- Установите истинность высказывания:
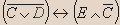
Решение.
| C | D | E | 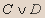 | 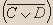 | 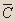 | 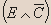 | 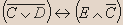 |
| 0 | 0 | 1 | |||||
| 0 | 1 | 0 | |||||
| 1 | 0 | 0 | |||||
| 1 | 0 | 1 | |||||
| 1 | 1 | 0 | |||||
| 1 | 1 | 1 |
Вывод. Из таблицы видно, что высказывание истинно всегда, кроме случая, когда:
1. C 0; D
0; D  0; E
0; E  0;
0;
2. C 0; D
0; D  1; E
1; E  1;
1; - Для формулы придумайте формализуемое ею высказывание:
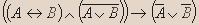
Решение.
Пусть:
A— «Алеша читает книгу»
B— “Дима учит уроки”
Если тогда и только тогда Алеша читает книгу, когда Дима учит уроки, и неверно что Алеша читает книгу или Дима учит уроки, то Алеша не читает книгу или Дима не учит уроки. - Данное высказывание преобразуйте в эквивалентное, но уже не содержащее отрицаний сложных высказываний:

Решение.
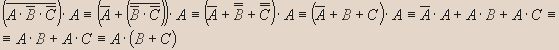
- Упростите:
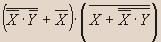
Решение.

Вариант №3.
- Докажите эквивалентность:
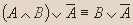
Решение.
| A | B | 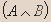 | 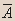 | 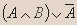 | 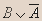 |
- Вывод.Из таблицы видно, что

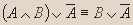
- Докажите, является ли данное высказывание тавтологией:
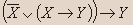
Решение.
| X | Y | 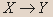 | 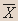 |  | 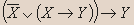 |
Вывод.Из таблицы видно, что высказывание не является тавтологией.- Установите истинность высказывания:
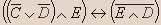
Решение.
| C | D | E | 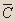 | 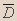 | 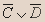 | 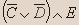 | 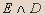 |  | 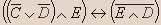 |
| 0 | 0 | 1 | |||||||
| 1 | 0 | 1 | |||||||
| 1 | 1 | 1 |
Вывод. Из таблицы видно, что высказывание истинно когда:
1. C 0; D
0; D  0; E
0; E  1;
1;
2. C 1; D
1; D  0; E
0; E  1;
1;
3. C 1; D
1; D  1; E
1; E  1;
1; - Для формулы придумайте формализуемое ею высказывание:
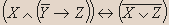
Решение.
Пусть:
X— «Даша идет в кино»
Y— “Оля поет”
Z—“Олег танцует”
Тогда и только тогда Даша идет в кино и если Оля не поет, то Олег танцует, когда неверно что Даша идет в кино или Олег танцует. - Данное высказывание преобразуйте в эквивалентное, но уже не содержащее отрицаний сложных высказываний:
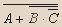
Решение.

- Упростите:
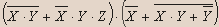
Решение.
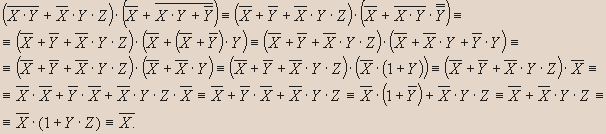
Вариант №4.
- Докажите эквивалентность:
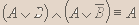
Решение.
| A | B | 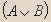 | 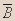 | 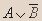 | 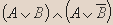 |
Вывод. Из таблицы видно, что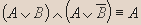
- Докажите, является ли данное высказывание тавтологией:
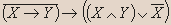
Решение
| X | Y | 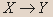  |  | 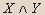 | 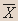 | 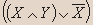 | 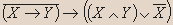 |
Вывод.Из таблицы видно, что высказывание не является тавтологией.- Установите истинность высказывания:
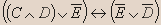
Решение.
| C | D | E | 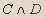 | 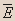 | 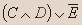 | 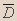 | 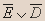 | 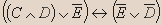 |
| 0 | 0 | 0 | ||||||
| 0 | 1 | 0 | ||||||
| 0 | 1 | 1 | ||||||
| 1 | 0 | 0 | ||||||
| 1 | 1 | 0 | ||||||
Вывод.Из таблицы видно, что высказывание истинно всегда, кроме случая:
1. C 0; D
0; D  0; E
0; E  1;
1;
2. C 1; D
1; D  0; E
0; E  1;
1;
3. C 1; D
1; D  1; E
1; E  1;
1; - Для формулы придумайте формализуемое ею высказывание:
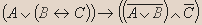
Решение.
Пусть:
A— «Коля пишет письмо»
B— “Дима смотрит телевизор”
C—“Игорь разговаривает по телефону”
Если Коля пишет письмо или тогда и только тогда Дима смотрит телевизор, когда Игорь разговаривает по телефону, то неверно что, Коля пишет письмо или Дима смотрит телевизор и Игорь не разговаривает по телефону. - Данное высказывание преобразуйте в эквивалентное, но уже не содержащее отрицаний сложных высказываний:

Решение.
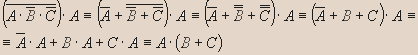
- Упростите:
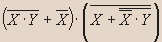
Решение.
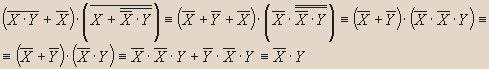
РЕШЕНИЕ ЛОГИЧЕСКИХ ЗАДАЧ.
Наглядность и оборудование: файлы ЗАГОТОВКА_ЛОГИКА.XLS, ЛОГИКА.XLS (logika\2\11klass\file\urok11-12\...).
План урока.
- Проверка д.з.
- Решение задач.
Ход урока.
I. Проверка домашнего задания.
В спортивных соревнованиях принимали участие пять пионерских команд: "Вымпел", "Метеор", "Нептун", "Старт" и "Чайка". Об их итогах соревнования имеется пять высказываний:
- Второе место занял "Вымпел", a "Старт" оказался на третьем.
- Хорошо выступала команда "Нептун", она стала победителем, а "Чайка" вышла на второе место.
- Да нет же, " Чайка" заняла только третье место, а "Нептун"- был последним.
- Первое место по праву завоевал "Старт", а "Метеор" был четвертым.
- Да, "Метеор" действительно был четвертым, а "Вымпел" был вторым.
Известно, что команды не делили места между собой и что в каждом высказывании одно утверждение правильное, а другое нет.
Как распределились места между командами?
Решение.Введем обозначения B- Вымпел, N - Нептун, C - Старт, H - Чайка, M - Метеор. Цифры означают места. Согласно высказываниям составим уравнения:

Ответ. Из полученного выражения следует, что команды заняли следующие места: "Вымпел" - 1, "Метеор" - 4, "Нептун" - 5, "Старт" - 3, "Чайка" - 2.
II. РЕШЕНИЕ ЗАДАЧ.
Распределить группу учащихся на 4 подгруппы. Распределить задачи.
Задача №1.
На ледяном поле 5 хоккеистов: Ольховский, Малышев, Белов,
Таманин, Лавров - штурмовали ворота. Раздался свисток судьи.
"Удаляет двух", - подумали спортсмены. "Без Малышева или Ольховского я не останусь на поле", - сказал Таманин. "Я тоже, "- сказал Лавров. "Удаляют либо меня с Беловым, либо Таманина с Лавровым", - сказал Малышев. Когда судья объявил о своем решении все оказались правы и кроме того Ольховский и Белов не остались вместе на поле. Кто остался на поле ?
Решение.Введем буквенные обозначения: O - Ольховский, M - Малышев,
B - Белов, T - Таманин, L - Лавров. Высказывания каждого хоккеиста можно задать формулами :
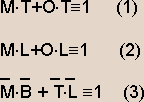
Для решения системы логических уравнений умножим уравнение (1) на уравнение (2):
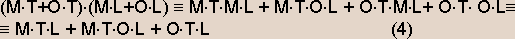
Полученное выражение (4) умножим на уравнение (3):
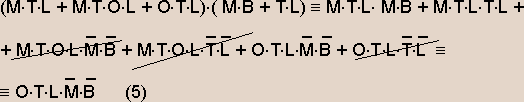
Из полученного выражения (5) следует, что на поле остались Ольховский, Таманин, Лавров.
Графическое дерево.
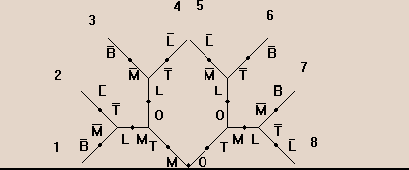
Проанализировав все ветви графического дерева, можно сделать заключение, что единственно правильным решением является ветвь 5.
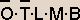
Алгоритм.
алг Задача (цел F1,F2,F3,T,O,M,L,B,F)
арг F1,F2,F3,T,O,M,L,B
рез F
нач
1: T:=0
2: O:=0
3: M:=0
4: L:=0
5: B:=0
6: F1:=(M и Т) или (О и Т)
F2:=(М и L) или (О и L)
F3:=(не М и не В) или (не Т и не L)
F:=F1 и F2 и F3
если F=1
то вывод F,T,O,M,B,L
все
если В<1
то B:=1: переход к 6
все
если L<1
то L:=1:переход к 5
если М<1
то М:=1:переход к 4
все
если О<0
то О:=1:переход к 3
все
если Т<1
то Т:=1:переход к 2
все
кон
Бейсик-программа.
CLS
10 T=0
20 O=0
30 M=0
40 L=0
50 B=0
60 F1=(M AND T) OR (O AND T)
70 F2=(M AND L) OR (O AND L)
80 F3=(NOT M AND NOT B) OR (NOT T AND NOT L)
90 F=F1 AND F2 AND F3
100 IF F=1 THEN ?" F ";" T ";" O ";" M ";" L ";" B ":?F;T;O;M;L;B
110 IF B<1 THEN B=1: GOTO 60
120 IF L<1 THEN L=1: GOTO 50
130 IF M<1 THEN M=1: GOTO 40
140 IF O<1 THEN O=1: GOTO 30
150 IF T<1 THEN T=1: GOTO 20
160 END
Паскаль-программа.
program zad1;
uses crt;
var t,o,m,b,l:boolean;
function func:boolean;
var f:array[1..3] of boolean;
begin
f[1]:=(m and t) or (o and t);
f[2]:=(m and l) or (o and l);
f[3]:=(not m and not b) or (not t and not l);
func:=f[1] and f[2] and f[3];
end;
procedure ff(i:integer);
begin
case i of
1:begin
t:=false;ff(i+1); t:=true;ff(i+1);
end;
2:begin
o:=false;ff(i+1); o:=true;ff(i+1);
end;
3:begin
m:=false;ff(i+1); m:=true;ff(i+1);
end;
4:begin
l:=false;ff(i+1); l:=true;ff(i+1);
end;
5:begin
b:=false;ff(i+1); b:=true;ff(i+1);
end;
6:begin
if func=true then
begin
writeln(' f t o m l b ');
writeln(func,' ',t,' ',o,' ',m,' ',l,' ',b);
end;
end; end; end;
begin
ff(1);
end.
Задача №2.
Перед началом забегов зрители обсуждали скаковые возможности трех лучших лошадей с кличками "Абрек", "Ветер", "Стрелок".
- Победит или "Абрек", или "Стрелок", - сказал один болельщик.
- Если "Абрек" будет вторым, то победу принесет "Ветер", - сказал другой болельщик.
- Много вы понимаете в лошадях, - возмутился третий болельщик.
- Вторым придет или 'Ветер", или "Абрек".
- А я вам скажу, - вмешался четвертый болельщик, - что если "Абрек" придет третьим, то "Стрелок" не победит.
После забега выяснилось, что три лошади - "Абрек", "Ветер" и "Стрелок" - заняли три первых места, не деля между собой ни одного из мест, и что все четыре предсказания болельщиков были правильны. Как кончился забег?
Решение. Обозначим клички лошадей буквами: A - "Абрек", B - "Ветер", C- "Стрелок". Высказывания каждого болельщика о спортсменах можно задать формулами :
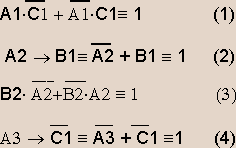
По условию задачи лошади заняли три первых места, не деля между собой ни одного места. Зададим эти условия уравнениями (5) - (8):

Ответ.Из полученного выражения следует, что "Абрек" занял 1 место, "Ветер" - 2 место, "Стрелок" - 3 место (первым не может быть по условию задачи).
