Модель Харрисона-Руззо-Ульмана
Разработан в 1971 году и формализует матрицу доступа
М – матрица прав доступа
Q – текущее состоянии системы
Q(S,O,M)
М(S,O) – ячейка матрицы, содержащая набор прав доступа субъекта S к объекту O
Поведение системы во времени моделируется переходами между различными ее состояниями. Переходы осуществляются путем внесения изменений в матрицу M с использованием команд следующего вида:
Command a(x1,xk)
if r1 in M[Xs1,Xo1] and
if r2 in M[Xs2,Xo2] and
…
if rm in M[Xsm,Xom] and
then
op1
op2
…
a – Имя команды
xi – параметры команды, представляющие идентификаторы субъектов и объектов
opi – элементарные операции, которые будут выполнены в том случае, если выполняются все без исключения условия из блока if … then.
В результате выполнения операции команда переходит из состояния Q=(S,O,M) в состояние Q’=(S’,O’,M’).
Модель предусматривает наличие 6 элементарных операций
1) Enter r into M[s,o] (s*принадлежит*S,o*принадлежит*O)
Добавление к субъекту S права r по отношению к объекту O. В результате выполнения команды происходит следующее изменение в состоянии системы:
S’=S
O’=O
M’[xs,xo]= M[xs,xo], если (xs,xo) не равно (s,o)
M’[s,o]= M’[s,o]v{r}
2) Delete r from M[s,o] (s*принадлежит*S,o*принадлежит*O)
Удаление у субъекта S права r по отношению к объекту O
S’=S
O’=O
M’[xs,xo]= M[xs,xo], если (xs,xo) не равно (s,o)
M’[s,o]= M’[s,o]\{r}
3) Create subject s (s#не принадлежит#S)
Создание нового субъекта s
O’=Ov{s}
S’=S v{s}
M’[xs,xo]= M[xs,xo] для любых (xs,xo)#принадлежащих#S*O
M’[s,xo]=#не пустое множество# для любых xo#принадлежащих#O’
M’[s,xo]=#не пустое множество# для любых xs#принадлежащих#S’
4) Destroy subject s (s#принадлежит#S)
Удаление существующего субъекта s
S’=S\{s}
O’=O\{s}
M’[xs,xo]= M[xs,xo] для любых (xs,xo)#принадлежащих#S*O
5) Create object o (o#не принадлежит#O)
O’=Ov{o}
S’=S
M’[xs,xo]= M[xs,xo] для любых (xs,xo)#принадлежащих#S*O
M’[xs,o]=#не пустое множество# для любых xs#принадлежащих#S’
6) Destroy object o (o#принадлежит#O)
Удаление существующего объекта o
O’=O\{o}
S’=S
M’[xs,xo]= M[xs,xo] для любых (xs,xo)#принадлежащих#S’*O’
Пример
1. Создание файла
command create_file (p,f)
create object f
enter own into M[p,f]
enter r into M[p,f]
enter w into M[p,f]
end
создает объект own, наделяет пользователя правами чтения и записи.
2. Создание процесса (процесс p создает процесс q и получает на него права чтения, записи и владения, передавая процессу q права записи и чтения по отношению к самому себе)
command exec_process (p,q)
create subject q
enter own into M[p,q]
enter r into M[p,q]
enter w into M[p,q]
enter r into M[q,p]
enter w into M[q,p]
end
3. Передача права чтения по отношению к файлу. Право чтения на файл f передается владельцем p субъекту q
command grand_read (p,q,f)
if own in M[p,f]
then
enter r into M[q,f]
end
Формальное описание системы в модели Харрисона-Руззо-Ульмана выглядит следующим образом
#Система#=(Q,R,C)
Состоит из следующих элементов:
1) Конечный набор прав доступа R={r1,…,rn}
2) Конечный набор исходных субъектов So={s1,…,sn}
3) Конечный набор исходных объектов Oo={o1,…,on}
4) Исходная матрица доступа Mo
5) Конечный набор команд C={ai(x1,…,xk)}
Поведение системы во времени рассматривается как последовательность состояний {Qi}, каждое последующее состояние является результатом применений некоторой команды к предыдущей.
… Чётотам…
Покажем, является ли заданная система с некоторым начальным состоянием безопасной относительно того или иного права доступа для частного случая. Система E=(Q,R,C)называется монооперационной, если каждая команда ai#принадлежит#С выполняет один примитивный оператор
Th:
Существует алгоритм, который проверяет исходное состояние монооперационной системы безопасным для данного права А.
Доказательство:
Покажем, что число последовательностей команд системы, которые необходимо проверить, является ограниченным. В этом случае проверка безопасности системы сведется к полному перебору всех последовательностей и к проверке конечного состояния каждой из них на отсутствие утечки права А. Нет необходимости рассматривать более одного оператора create, т.к. система является монооперационной и одна команда не может одновременно создать объект или субъект и модифицировать его права доступа, поскольку путем замены параметров можно ограничиться работой с последовательностями команд, которые оперируют над существующими объектами или субъектами. Единственная команда create будет необходима на случай, если в начальном состоянии в системе не было ни одного субъекта.
Пусть С1,С2,…,Сn – последовательность команд, в результате выполнения которой происходит утечка права А. Упростим эту последовательность команд следующим образом:
1) Удалим все команды Delete и Destroy.
2) Добавим в начало последовательности С1,С2,…,Сn команду Sinit следующего вида: create subject.
3) Проходя последовательность команд справа налево, последовательно удалим все команды вида create subject, заменяя ссылки на создаваемые с помощью этих команд объекты ссылками на Sinit.
4) Аналогично удалим все команды вида create object, заменяя на Sinit.
5) Удалим все команды вида enter, вносящие право А в ячейку, которая уже содержит это право.
Получившаяся в результате данных преобразований последовательность команд также приводит к утечке права А. Проанализируем состав возможных команд получившейся последовательности. Команды вида create object, destroy subject, destroy object и delete в ней отсутствуют.Команда create subject присутствует в единственном числе. Максимальное число команд вида enter равно |R|(|S0|+1)(|O0|+1), а общее число возможных команд равно |R|(|S0|+1)(|O0|+1)+1, а значит количество последовательностей команд ограничено, что и требовалось доказать.
К сожалению расширить подобный результат на произвольные системы невозможно.
Th:
Для систем общего вида задача определения того, является ли исходное состояние системы безопасным для данного права А, является вычислительно неразрешимой. Для доказательства достаточно свести задачу проверки безопасности системы к заведомо неразрешимой задаче остановки машины тьюринга.
Модель Белла-Ла Падулле
В модели Белла-Ла Падулле по грифам секретности распределяются субъекты и объекты, действующие в системе и при этом выполняются следующие правила:
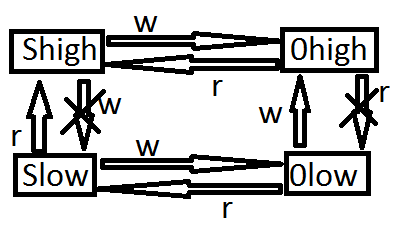
1) Простое правило безопасности, Simple Security (SS) – Субъект с уровнем секретности Xs может читать информацию из объекта с уровнем секретности X0 тогда и только тогда, когда Xs преобладает над X0; «no read up»
2) * - свойство (property) – субъект с уровнем секретности Xs может писать информацию в объект с уровнем секретности X0 тогда и только тогда, когда X0 преобладает над Xs. «no write down»
S#принадлежит#O
R={r,w}
L={u,su,s,ts} (unclassified, sensitive but unclassified, secret, top secret)
#дельта# - решетка уровня секретности.
V – множество состояний системы, представляемое в виде набора упорядоченных пар (F,M)
F: SvO->L, где F – функция уровня секретности, ставящая каждому объекту и субъекту в системе в соответствие определенный уровень секретности.
M = матрица текущих прав доступа
#дельта# (L, <= ,#жирная точка#,#крестик в кружочке#)
<= - оператор, определяющий частичное нестрогое отношение порядка для уровней секретности
#жирная точка# - оператор наименьшей верхней границы
#крестик в кружочке# - оператор наибольшей нижней границы
Отношение, имеющее <=, обладает следующими свойствами:
1) Рефлексивность (#для любых# а #принадлежит# L:а <= а)
Разрешена передача информации между субъектами и объектами одного уровня секретности.
2) Антисимметричность
(#для любых# а1,a2 #принадлежит# L:(( а1 <= а2)&(a2<=a1))->a2=a1)
В данном случае это означает, что информация может передаваться как от субъектов и объектов уровня А к субъектам и объектам уровня В, так и от субъектов и объектов уровня В к субъектам и объектам уровня А, в таком случае эти уровне эквивалентны.
3) Транзитивность
(#для любых# а1,a2,a3 #принадлежит# L: (( а1 <= а2)&(a2<=a3))->a1<=a3)
Транзитивность означает, что если информация может передаваться от субъектов и объектов уровня А к субъектам и объектам уровня В, а от субъектов и объектов уровня В к субъектам и объектам уровня С, то информация также может передаваться от субъектов и объектов уровня А к субъектам и объектам уровня С.
Операторы наибольшей нижней #крестик в кружочке# и наименьшей верхней #жирная точка# границы определяются следующим образом:
а=а1#жирная точка#a2<=>(а1,a2<=a)&(#любой#a’#принадлежит#L:(a’<=a)->(a’<=a1Va’<=a2))
а=а1#крестик в кружочке#a2 <=> <=>(a<=а1,a2)&(#любой#a’#принадлежит#L:(a’<=a1)&(a’<=a2)->(a’<=a))
Для каждой пары существует единственный элемент наименьшей верхней границы и единственный элемент наибольшей нижней границы.
Система ∑=(V0,R,T) в данной модели состоит из следующих элементов:
V0 – начальное состояние системы
R – множество прав доступа
T:VxR->V – функция перехода, которая в ходе выполнения запросов переводит систему из одного состояния в другое
Изменение состояния системы происходит следующим образом:
Система, находящаяся в состоянии v#принадлежит#V, получает запрос на доступ r#принадлежит#R и переходит в состояние V*=T(v,r). Состояние Vn называется достижимым для системы ∑, если существует последовательность:
{(Z0,V0),…,(Zn-1,Vn-1),(Zn,Vn)}:T(Zi,Vi)=Vi+1,#любой#i=0,n-1
Начальное состояние V0 является достижимым по определению.
Состояние системы (F,M) называется безопасным по чтению или Simple-безопасным, если для каждого субъекта, осуществляющего в этом состоянии доступ по чтению к объекту, уровень безопасности субъекта доминирует над уровнем безопасности объекта.
#любой#s#принадлежит#S, #любой#o#принадлежит#O,
z#принадлежит#M[s,o]->F(o)<=F(s)
#любой#s#принадлежит#S, #любой#o#принадлежит#O,
w#принадлежит#M[s,o]->F(s)<=F(o)
Состояние (F,M) называется безопасным по записи в случае, если для каждого субъекта, осуществляющего в этом состоянии доступ по записи к объекту, уровень безопасности объекта доминирует над уровнем безопасности субъекта.
Состояние (F,M) называется безопасным, если оно безопасно по чтению и по записи. Полностью система ∑=(V0,R,T) называется безопасной, если ее начальное состояние V0 безопасно и все состояния, достижимые из V0 путем применения конечной последовательности запросов из R безопасны.
Основная теорема безопасности Беллы-Ла Падулле
Система ∑=(V0,R,T) безопасна тогда и только тогда, когда выполнены следующие условия:
1) Начальное состояние V0 безопасно
2) Для любого состояния V, достижимого из V0, путем применения конечной последовательности запросов из R таких, что
T(v,z)=V*
v=(F,M)
V*=(F*,M)
для #любой#s#принадлежит#S,
#любой#o#принадлежит#O
Выполнены условия:
a. If z#принадлежит#M*[s,o] и z#не принадлжит#M[s,o] then F*(o)<=F*(s)
b. If z#принадлежит#M[s,o] и F*(s)< F*(o), then z#не принадлжит#M*[s,o]
c. If w#принадлежит#M*[s,o] и w#не принадлжит#M[s,o] then F*(s)<=F*(o)
d. If w#принадлежит#M[s,o] и F*(o)< F*(s), then w#не принадлжит#M*[s,o]
Пусть система ∑=(V0,R,T) безопасна.
V0 безопасно по определению
Предположим, что существует такое безопасное состояние V*, достижимое из состояния V:T(v,r)=V*
Допустим, для данного состояния нарушено одно из условий (a-d), во всех случаях мы получаем противоречия с тем, что состояние V* является безопасным. Покажем достаточность утверждения.
Система ∑=(V0,R,T) может быть небезопасна в двух случаях:
1) В случае, если изначальное состояние V0 небезопасно (противоречит условию теоремы).
2) В случае, если существует небезопасное состояние V*, достижимое из безопасного V0 путем применения конечного числа запросов из R. Это означает, что на каком-то этапе произошел переход Т(v,r)=V*, где v – безопасное состояние, а V* - небезопасное, однако условия (a-d) делают данный переход невозможным.
ЧТД
Формальные модели целостности
Модель Кларка-Вилсона (1987)
S – множество субъектов
D – множество данных в АС
CDI (constrained data items) – данные, целостность которых контролируется
UDI (un constrained data items) – данные, целостность которых не контролируется
D=CDI#чашка (cup)#UDI
CDI#шапка (hat)#UDI=#пустое множество#
TP (transformation procedure) компонент, способный инициировать транзакцию
Транзакция – последовательность действий, переводящая систему из одного состояния в другое
IVP (integrity verification procedure) – процедура проверки целостности CDI
Правила модели Кларка-Вилсона:
1) В системе должны иметься IVP, способные подтвердить целостность любого CDI
2) Применение любой TP к любому CDI должно сохранить целостность этого CDI
3) Только TP могут вносить изменения в CDI
4) Субъекты могут инициировать только определенные TP над определенными CDI (система должна поддерживать отношения вида (s,t,d), где s,t,d соответственно принадлежат S,TP,CDI)
5) Должна быть обеспечена политика разделения обязанностей субъектов, то есть субъекты не должны изменять CDI без вовлечения в операцию других субъектов системы
6) Специальные TP могут превращать UDI в CDI
7) Каждое применение TP должно регистрироваться в специальном CDI, при этом:
a. Данный CDI должен быть доступен только для добавления информации
b. В данный CDI необходимо записывать информацию, достаточную для восстановления полной картины функционирования системы
8) Система должна распознавать субъекты, пытающиеся инициировать TP
9) Система должна разрешать производить изменения в списках авторизации только специальным субъектам
Модель Биба (1977)
Модификация Беллы-Ла Падулле для целостности данных.
#дельта#=(IC, <=, #жирная точка#, #крестик в кружочке#) решетка классов целостности
IC – Классы целостности данных
Базовые правила модели Биба:
1) Простое правило целостности (Simple integrity, SI) – субъект с уровнем целостности Xs может читать информацию из субъекта с уровнем целостности X0 тогда и только тогда, когда X0 преобладает над Xs (No read down)
2) * - свойство (integrity) – субъект с уровнем целостности Xs может писать информацию в объект с уровнем целостности X0 тогда и только тогда, когда Xs преобладает над X0 (No write up)
Диаграмма информационных потоков
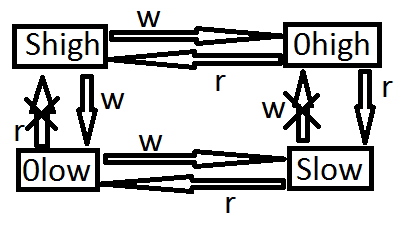
В большинстве приложений целостность данных рассматривается как некое свойство, которое либо сохраняется, либо не сохраняется и введение иерархических уровней целостности может представляться излишним. В действительности же уровни целостности в модели Биба стоит рассматривать как уровни достоверности, а соответствующие информационные потоки как передачу информации из более достоверной совокупности данных в менее достоверную и наоборот. Формальное описание модели Биба полностью аналогично описанию модели Белла-Ла Пудуллы. К достоинствам данной модели следует отнести ее простоту, а так же использование хорошо изученного мат. аппарата, недостатки аналогичны модели Белла-Ла Падуллы.
