Характеристические числа графов

Цикломатическое число. Пусть задан граф без петель. Цикломатическим числом графа называют величину V(G)=r-n+P,где n - число вершин графа, r - число его ребер, P - число компонент связности. Так как n-P=R(G)- ранг графа, то V(G) = r-R(G).

Цикломатическое число соответствует тому наименьшему количеству ребер в графе, которые нужно исключить из графа, чтобы получить дерево.

Хроматическое число. Пусть задан граф без петель: G(X,Г). Разобьем множество его вершин на Кнепересекающихся подмножеств так, чтобы любые две смежные вершины x_i,x_jÎXпринадлежали разным подмножествам ,т.е. чтобы ребра графа G(X,Г) соединяли вершины из разных подмножеств: "x_iÎX [x_iÎXs ®Гx_iÏXs]. Отметим все вершины Xиндексами 1,2,...,K(т.е. раскрасим вершины Kцветами), причем вершины внутри каждого подмножества Xпомечают одним индексом (раскрашивают одним цветом). Подмножества формируют таким образом, чтобы концы любого ребра графа имели различные индексы. Наименьшее возможное число подмножеств, получаемое в результате такого разбиения вершин графа G(X,Г), называют хроматическим числом графа, К(G), а граф G(X,Г) называют К-хроматическим.

Особое значение имеет бихроматический граф или двудольный граф, для которого К(G)=2. Согласно теореме Кенига обыкновенный граф является бихроматическим тогда и только тогда, когда он не содержит циклов нечетной длины. Если граф - дерево, т.е. в нем нет циклов, то он является бихроматическим графом.

Определение хроматического числа осуществляется с помощью сравнительно сложных алгоритмов. Для простых связных графов оценить число К(G) можно следующим образом. Сначала выбираем вершину с минимальной степенью и пометим (раскрасим) ее, затем произведем раскраску вершин, смежных с данной и т.д. Например, для графа, изображенного на рис.16, выбираем вершину x₃, для которойr(x₃)=1, и пометим ее красным цветом. Вершину x₂ можно раскрасить в синий цвет, а вершины x₁ и x₅ - в красный (они не смежны с x₃). Вершины x₆иx₈можно раскрасить в синий цвет.

Оставшиеся вершины x₄иx₇раскрасим в зеленый цвет. Всего использовано 3 цвета. Значит К(G)=3.

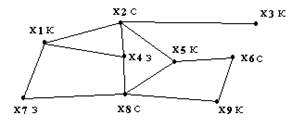
Рис. 16. Определение хроматического числа графа

Плоские графы

Граф называется плоским (планарным), если он может быть изображен на плоскости так, что все его ребра пересекаются только в вершинах графа. Планарность является внутренним свойством графа и не обязательно проявляется при произвольном его изображении.

Максимальное число некратных ребер у плоского графа r_max=3(n-2). Если число таких некратных ребер графа r£n+2, то такой граф заведомо плоский. Таким образом, можно записать условия для предварительного исследования планарности графа:

r>3(n-2) - граф заведомо не плоский,

r£n+2 - граф заведомо плоский.

Если число некратных ребер графа находится в интервале n+2<r£3(n-2), то для выяснения его планарности требуются специальные исследования.

Согласно теореме Понтрягина-Куратовского граф является плоским тогда и только тогда, когда он не содержит подграфа, изоморфного с точностью до вершин степени два одному из графов Понтрягина-Куратовского. Графы Понтрягина-Куратовского первого и второго типов приведены на рис. 17. Эти графы заведомо не плоские и имеют минимум одно пересечение ребер.

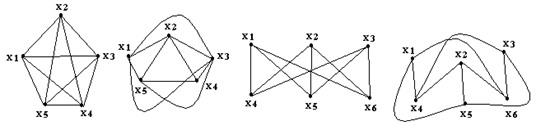
Рис. 17. Графы Понтрягина-Куратовского

Литература

1. Деньдобренько В.Н., Малика А.С. Автоматизация конструирования РЭА.-М.: Высшая школа, 1980.-361 с.;ил.

2. Коршунов Ю.А. Математические основы кибернетики: Учеб. пособие для вузов, - М.:Энергоатомиздат,1987. -496 с.;ил.

3. Сигорский В.П. Математический аппарат инженера. - К.: Техника, 1975.- 766с.;ил.