Признак равносильности формул 1 страница

Министерство образования и науки Российской Федерации

Нижнекамский химико-технологический институт (филиал)

Федерального государственного бюджетного образовательного

Учреждения высшего профессионального образования

Казанский национальный исследовательский технологический

университет»

А.В. Садыков, Е.С. Титова

Математическая логика

и теория алгоритмов

Часть I

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

Нижнекамск

2016

УДК 510.6

С 14

Печатается по решению редакционно-издательского совета НХТИ ФГБОУ ВПО «КНИТУ».

Рецензенты:

Саримов Н.Н., кандидат физ.-мат. наук, доцент;

Апайчева Л.А.,кандидат физ.-мат. наук, доцент.

Садыков, А.В.

С 14Математическая логика и теория алгоритмов. Часть I: Методические указания / А.В. Садыков, Е.С. Титова. – Нижнекамск : НХТИ ФГБОУ ВПО «КНИТУ», 2016. – 60 с.

В работе приводятся основные базовые понятия по разделам математической логики. Излагаемый материал сопровождается примерами и дополняется упражнениями.

Методические указания могут быть использованы при организации самостоятельной работы студентов.

Предназначены для студентов, обучающихся по направлениям подготовки бакалавров «Информатика и вычислительная техника», «Управление в технических системах», «Автоматизация технологических процессов и производств».

Подготовлены на кафедре математики Нижнекамского химико-технологического института.

УДК 510.6

© Садыков А.В., Титова Е.С., 2016

© НХТИ ФГБОУ ВПО «КНИТУ», 2016

1. ЛОГИКА ВЫСКАЗЫВАНИЙ

1.1. Высказывания и операции над ними

Определение 1. Высказывани­е – связное повествовательное предложение, о котором можно сказать истинно оно или ложно.

Примеры.

А₁ – " 8 < 5 "

А₂ – " Город Саратов находится на берегу Волги "

А₃ – " Слава российским космонавтам! "

В приведенных примерах высказываниями являются А₁, А₂, причем А₁ – ложное высказывание, А₂ – истинное высказывание. А₃ не является высказыванием, так как не является повествовательным предложением.

Высказывание можно рассматривать как величину, принимающую два значения: "истина" и "ложь". Высказывания будем обозначать латин­скими буквами, а их значения, то есть "истину" и "ложь", соответственно 1 и 0. Введем функцию l, заданную на совокупности всех высказываний и принимающую значения в множестве {0, 1}, по следующему правилу:

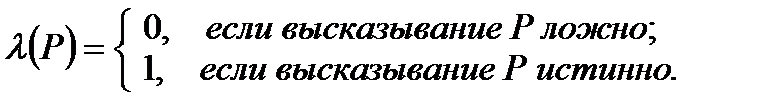
Функцию l называют функцией истинности, а значение 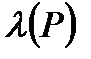для высказывания P – значением истинности или логическим значением высказывания P. Для приведенных высказываний имеем .

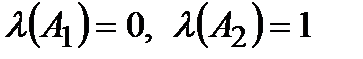Из элементарных высказываний с помощью логических операций строят сложные высказывания. В качестве основных в алгебре высказываний принято пять логических операций. Эти операции определяются следующим образом.

Определение 2. Конъюнкцией двух высказываний А, В на­зывается высказывание А˄В, которое истинно тогда и только тогда, когда истинны одновременно оба высказывания. Очевидно, в обыч­ной речи операции конъюнкции соответствует союз "и". Конъюнкцию еще обозначают символом ·, &.

Определение 3. Дизъюнкцией двух высказываний А, В на­зывается высказывание AÚB, которое ложно тогда и только тогда, когда ложны одновременно оба высказывания.

В обычной речи опе­рации дизъюнкции соответствует соединение высказываний связкой "или" с той лишь разницей, что AÚB согласно определению истинно и в случае, когда и А, и В оба истинны. Дизъюнкцию еще обозначают символом +.

Определение 4. Импликацией двух высказываний А, В на­зывается высказывание А®В, которое ложно тогда и только тогда, когда высказывание А истинно, а В ложно.

В обычной речи импли­кации соответствует связка "если ... то".

По определению при ложном А это высказывание истинно независимо от того, какое значение принимает В. В обычной речи подразумевается, что когда А ложно, то предложение "если А, то В" не имеет смысла.

Также по определению при истинном В высказывание А®В истинно независимо от того, какое значение принимает А. В обычной речи оба высказывания А и В могут быть истинными, но истинность В не выводится из истинности А как, например в пред­ложении "если калина красная, то снег белый".

Определение 5. Эквивалентностью двух высказываний А, В называется высказывание А«В, которое истинно тогда и только тогда, когда оба данных высказывания имеют одинаковые значения, то есть либо оба истинны, либо оба ложны. В обычной речи эквива­лентности соответствует связка "тогда и только тогда".

Определение 6. Отрицанием высказывания А называется высказывание 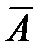, которое истинно тогда и только тогда, когда А ложно (другое обозначение: ).

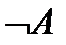Операция отрицания является унарной операцией, остальные – бинарными. Таблицы истинности этих операций имеют вид:

А В	А˄В	AÚB	А®В	А«В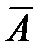
0 0
0 1
1 0
1 1

1.2. Формулы логики высказываний

Переменные, вместо которых можно подставлять высказывания, называют пропозициональными переменными или переменными высказываниями.

Понятие формулы в алгебре высказываний вводится индук­тивно.

Определение 7.

1. Переменные высказывания (пропозицио­нальные переменные) X, Y, Z, X_i, Y_i, Z_i (i Î N) и логические константы 0,1 – формулы.

2. Если F₁ и F₂ – формулы, то выражения 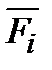(i = 1, 2), (F₁˄F₂), (F₁ÚF₂), (F₁®F₂), (F₁«F₂) также являются формулами.

3. Никаких других формул, кроме тех, которые образуются с помощью пунктов 1–2, нет.

Замечание 1.Для всякого выражения в алфавите {X, Y, Z, X_i, Y_i, Z_i (i Î N), , ˄, Ú, ®, «, (, )}, используя пункты 1, 2 оп­ределения 7, очевидно, можно выяснить, является оно формулой или нет.

Замечание 2. Соглашение о скобках. Для упрощения записи формул разрешается не писать:

а) внешние скобки;

б) скобки с учетом силы (приоритета) операции: самая сильная операция – отрицание (выполняется в первую очередь), затем в порядке следования – , ˄, Ú, ®, «.

Формулу, зависящую от переменных высказываний 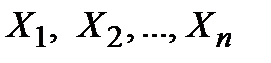, будем обозначать .

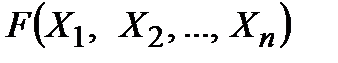Определение 8. Интерпретацией формулы 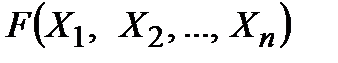называется высказывание 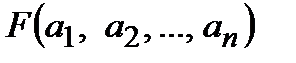, которое получается из заданной формулы после подстановки в нее вместо переменных 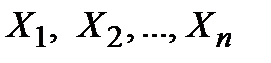соответственно конкретных высказываний .

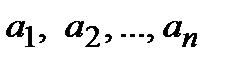1.3. Классификация формул.

Равносильные формулы

Определение 9.Формула 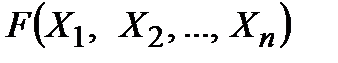называется выпол­нимой (опровержимой), если существует ее истинная (ложная) ин­терпретация.

Определение 10. Формула 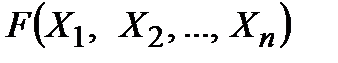называется тавтологией (противоречием), если любая ее интерпретация истинна (ложна). Если формула 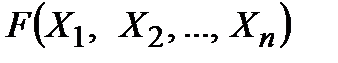является тавтологией, то пи­шут ╞ .

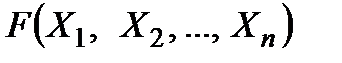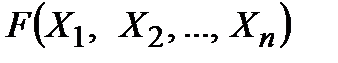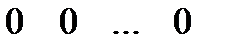
Нахождение всех возможных интерпретаций формулы связано с построением ее так называемой таблицы истинности. Таблица истинности формулы 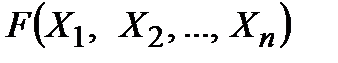строится следующим образом. Сначала выписываются слева все переменные высказывания 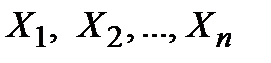, от которых зависит формула. Далее под ними выписываются все возможные наборы значений 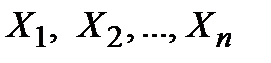. Обычно эти наборы выписываются в естественном порядке, то есть в по­рядке чисел, двоичными кодами которых являются соответствую­щие наборы. Построив, таким образом левый столбец, переходим к вычислению правого столбца, который обозначается через 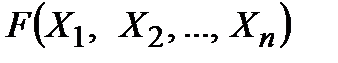. Итак, таблица истинности формулы 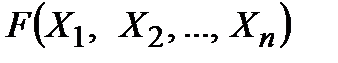выглядит следующим образом:

…	…
…	…

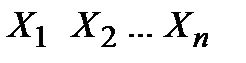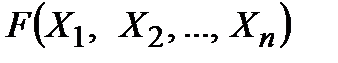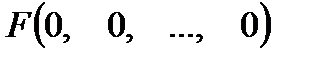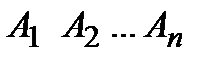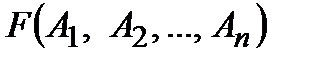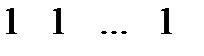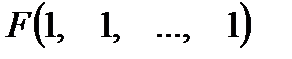На наборе 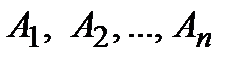справа выписывается интерпрета­ция формулы 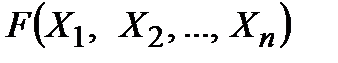для конкретных высказываний, имею­щих соответственно значения 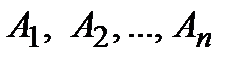. На практике обычно таблица истинности формулы 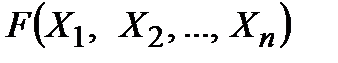строится постепенно в соответствии с ее структурой, то есть по мере выполнения соответст­вующих операций в формуле.

Пример.Построить таблицу истинности для формулы .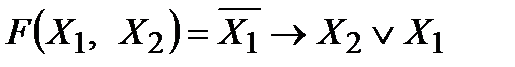

Решение.

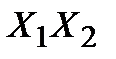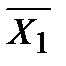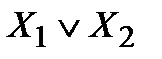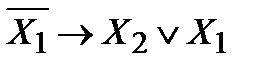0 0
0 1
1 0
1 1

Можно сформулировать следующую задачу: дать способ, позволяющий для каждой формулы конечным числом действий определить ее тип по приведенной (см. определения 9, 10) классификации. Поставленная задача носит название "проблемы разрешимости". Эта проблема, очевидно, легко решается построени­ем соответствующей таблицы истинности для формулы 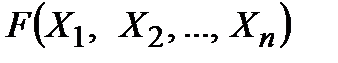, хотя число действий может оказаться очень большим, но оно конечно, в силу конечности (конечное число переменных и конечное число операций) формулы.

Определение 11. Две формулы 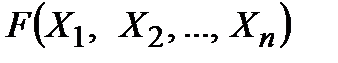, 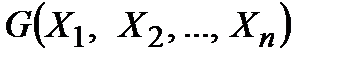называют равносильными, если для любых конкретных высказываний 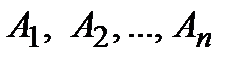их интерпретации совпадают, то есть .

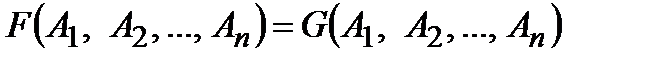Очевидно, равносильные формулы имеют одинаковые таб­лицы истинности. Бинарное отношение равносильности на множест­ве формул обозначают @.

Основные равносильности

1.Законы нуля и единицы

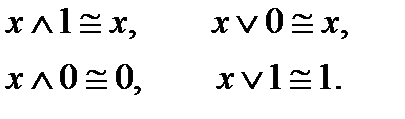
2.Закон двойного отрицания

.

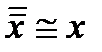3.Коммутативные (переместительные) законы

.

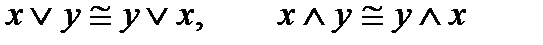4.Ассоциативные (сочетательные) законы

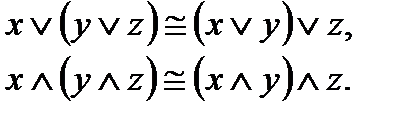
5.Дистрибутивные (распределительные) законы

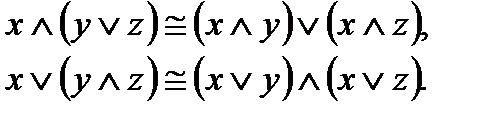
6.Законы де Моргана

.

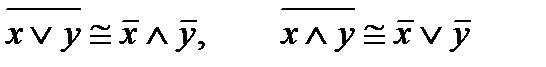7.Законы идемпотентности (одинаковости)

.

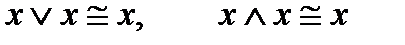8.Законы поглощения

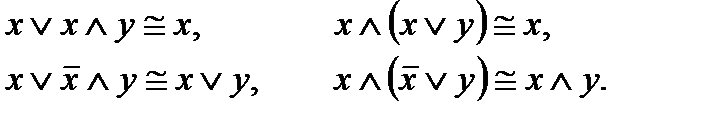
9.Закон исключенного третьего

.

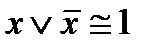10.Закон противоречия

.

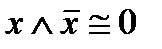Справедливость этих равносильностей легко проверяется с помощью сравнения таблиц истинности. Второй распределительный закон не имеет аналога в обычной алгебре, поэтому его часто называют «чудо-законом».

Упражнение 1. Доказать равносильности:

а) ;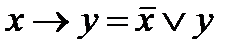

б) ;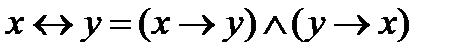

в) ;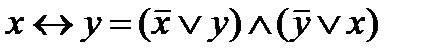

г) ;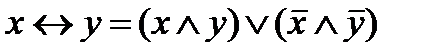

Лемма (о замене).Пусть 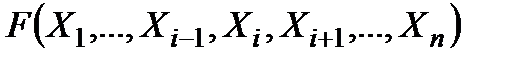- произвольная формула и .

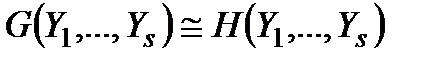Тогда 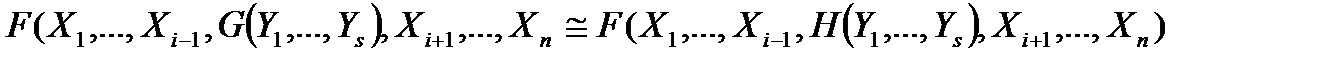Доказательство проводится непосредственным использованием определения равносильности формул. Эта лемма на практике позволяет осуществлять равносильные преобразования формул.

Признак равносильности формул

Теорема 1. Две формулы F и G алгебры высказываний равносильны тогда и только тогда, когда формула 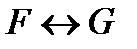является тавтологией:

╞ .

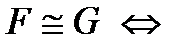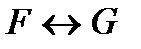Доказательствоследует непосредственно из определений 5, 11.

Закон двойственности

Определение 12. Пусть 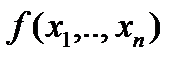– формула логики высказываний. Двойственной к ней называют формулу, определенную следующим образом

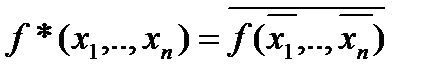
Замечание 3. Из закона двойного отрицания следует, что :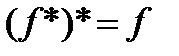

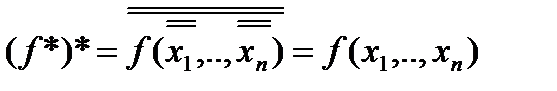
Теорема 2. Формулы 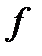и 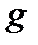равносильны тогда, и только тогда, когда двойственные им формулы 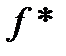и 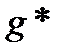тоже равносильны.

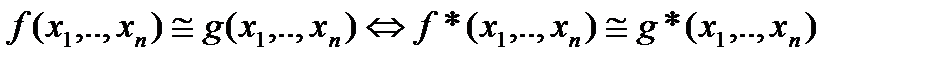, (1)

Доказательство. Пусть 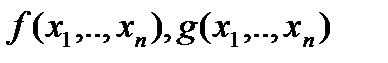– равносильны, а 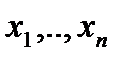– пропозицио­нальные переменные, входящие в эти формулы.

Из равносильност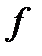и и 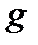следует:

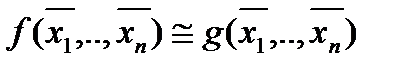, (2)

Из (2) следует

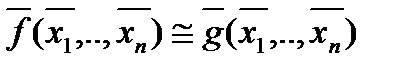, (3)

Отсюда

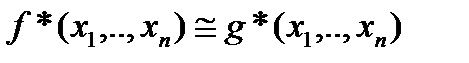, ч.т.д.

Замечание 4.Пусть формула 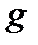получается из формулы f на основании первого дистрибутивного закона. Тогда переход от 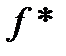к 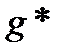осуществляется на основании второго дистрибутивного закона.

Замечание 5. То есть если переход 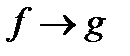на основании первого, то переход 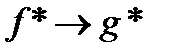на основании второго дистрибутивного закона.

Определение 13.Переход от 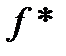к 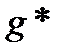называется преобразованием, двойственным преобразованию, переводящему f в .

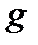Теорема 3 (Принцип двойственности). Двойственная к булевой формуле может быть получена заменой констант 0 на 1, 1 на 0, на , на и сохранением структуры формулы (то есть соответствующего порядка действий).

1.4. Нормальные формы

Введем обозначения

Пусть имеется набор пропозициональных переменных .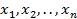

Определение 14. Формула 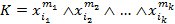, где 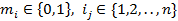, называется конъюнктивным одночленом (КО) или элементарной конъюнкцией.

Определение 15.Дизъюнкция КО 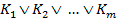называется дизъюнктивной нормальной формой (ДНФ).

Определение 16. Формула 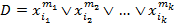, где 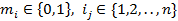, называется дизъюнктивным одночленом (ДО) или элементарной дизъюнкцией.

Определение 17.Конъюнкция КО 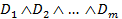называется конъюнктивной нормальной формой (КНФ).

Замечание 6. В определениях 14-16 никакие ограничения на переменные не накладываются.

Примеры.

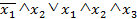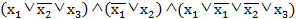– ДНФ

– КНФ

Замечание 7. Конъюнктивный одночлен (дизъюнктивный одночлен) называется еще элементарным произведением(элементарной суммой).

Всякую формулу можно выразить через конъюнкцию, дизъюнкцию и отрицание. Используя законы де Морганаи свойство дистрибутивности конъюнкции относительно дизъюнкции можно преобразовать равносильным образом получаемое выражение ДНФ. Если же к исходному выражению применить свойство дистрибутивности дизъюнкции относительно конъюнкции, то его можно свести к КНФ. Таким образом, справедлива теорема.

Теорема 4. Любая формула равносильными преобразованиями может быть приведена к ДНФ (КНФ).

Теорема 5. Формула 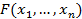является тавтологией (противоречием) тогда и только тогда, когда в ее КНФ (ДНФ) в каждом ДО (КО) некоторая переменная встречается вместе со своим отрицанием.

Совершенные нормальные формы

Среди нормальных форм важную роль играют совершенные нормальные формы.

Совершенная дизъюнктивная нормальная форма

Определение 18. Совершенной дизъюнктивной нормальной формой (СДНФ) формулы , содержащей n различных переменных, называется ее ДНФ, удовлетворяющая следующим условиям:

1) в ней нет двух одинаковых слагаемых;

2) ни одно слагаемое не содержит двух одинаковых множителей;

3) никакое слагаемое не содержит переменной вместе с ее отрицанием;

4) в каждом слагаемом в качестве множителя содержится либо переменная 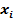, либо ее отрицание .

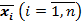Условия определения 18 позволяют получить правила, с помощью которых можно приводить формулу к СДНФ. Опишем эти правила.

Пусть дана произвольная формула . Процедура приведения к СДНФ:

1) Сначала приведём её к ДНФ. Пусть ДНФ для f – это формула 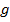(то есть ).

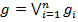2) Затем, если какое-нибудь слагаемое 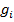не содержит переменной 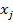, то добавим недостающую переменную:

,

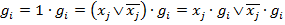Тогда условие 4) будет выполнено.

3) Если в полученном выражении окажутся одинаковые слагаемые, то, удалив все, кроме одного из них, получим равносильное выражение (используем закон идемпотентности ):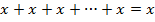

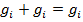
4) Если в некоторых слагаемых окажется несколько одинаковых множителей, то лишние множители можно удалить (используем закон ):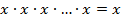

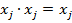
5) Удалим все слагаемые, которые содержат какую-либо переменную вместе с ее отрицанием ( 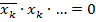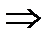такие слагаемые тождественно ложны).

Замечание 8. Если бы все слагаемые оказались таковыми, то вся сумма тождественно ложна. Тогда и формула f – тождественно ложна. В таком случае f не имеет СДНФ.