Прямые умозаключения логики высказываний

Основу умозаключений логики высказываний составляют смыслы (свойства) логических связок, объединяющих простые суждения в сложные. В таких умозаключениях не учитывается внутренняя структура входящих в посылки простых суждений.

Умозаключения логики высказываний бывают прямыми и непрямыми. Прямыми называют умозаключения, в которых заключение выводится из некоторого множества суждений. Непрямые – это умозаключения, которые получаются путём преобразования других умозаключений.

Выделяют следующие виды простых[6] форм прямых умозаключений логики высказываний:

1. Условно-категорические – умозаключения, в которых одна посылка – условное суждение, а вторая посылка и заключение – простые категорические. Условно-категорические умозаключения бывают двух разновидностей:

а) утверждающий модус (modus ponens):

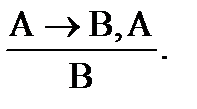
Например: Если человек простужен (А), то он болен (В).

Человек простужен (А).

Он болен (В).

б) отрицающий модус (modus tollens):

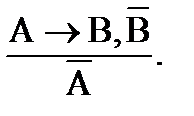
Например: Если человек простужен (А), то он болен (В).

Человек не болен (`В).

Он не простужен (`А).

(В схемах умозаключений над чертой записываются посылки, под чертой – заключение, черта означает «следовательно»; «А» и «В» – простые суждения).

Отметим, что сходные схемы:

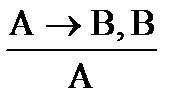
и

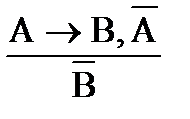
не являются правильными. Так, из посылок «Если человек простужен (А), то он болен (В)» и «Человек болен (В)» вовсе не обязательно следует «Он простужен (А)». «Человек болен» может означать, что у него сломана нога, поднялось давление и т.п. И только с определенной долей вероятности может оказаться, что он болен, потому что простужен. Аналогично для отрицающего модуса.

2. Разделительно-категорические – умозаключения, в которых одна посылка – разделительное суждение, а другая посылка и заключение – простые категорические. Разделительно-категорические умозаключения также бывают двух разновидностей:

а) утверждающе-отрицающая схема:

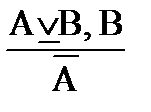или

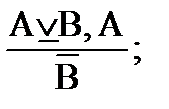
б) отрицающе-утверждающая схема:

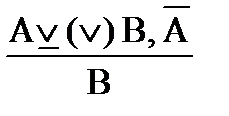или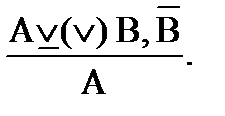

Например: Либо мы уходим (А), либо мы остаемся (В).

Мы не уходим (`А).

Мы остаемся (В).

3. Дилеммы (или условно-разделительные силлогизмы) – умозаключения, в которых заключение делается из трех посылок. Причем две из них – условные суждения, одна – разделительное. Заключениями дилемм могут быть как простые суждения (в простых дилеммах), так и сложные разделительные (в сложных дилеммах).

Существует четыре основных вида дилемм:

а) простая конструктивная дилемма:

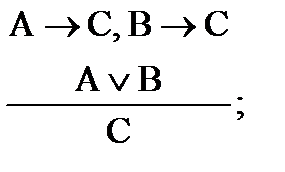
б) простая деструктивная дилемма:

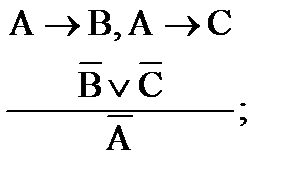
в) сложная конструктивная дилемма:

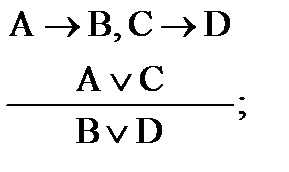
г) сложная деструктивная дилемма:

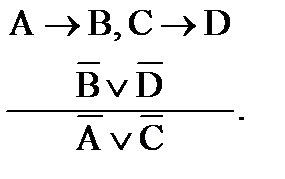
Например: «Если вы будете говорить правду (А), то люди проклянут вас (В), а если будете лгать (С), то вас проклянут боги (D). Но вы можете только говорить правду (A) или лгать (C). Значит, вас проклянут боги (D) или люди (B)». Если выписать из этого рассуждения древних философов буквенные обозначения простых суждений, соединив их соответствующими логическими связками, то получим форму сложной конструктивной дилеммы.

Кроме того, существуют конструктивно-деструктивные (или деструктивно-конструктивные) дилеммы. В таких дилеммах некоторые альтернативы разделительной посылки указывают на наличие оснований условных посылок, а некоторые отрицают следствия других условных посылок. Например, конструктивно-деструктивной является дилемма вида

.

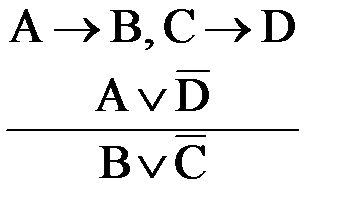4. Чисто условные умозаключения, представляющие собой вывод из любого количества посылок, при этом и посылки, и заключение в таких умозаключениях являются условными суждениями. Из всех умозаключений, относящихся к этому виду, чаще всего используются транзитивность импликации и правило контрапозиции.

Транзитивность импликации:

.

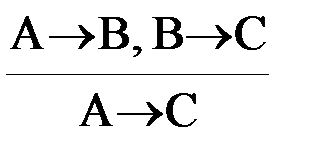Например: «Если лобная кора головного мозга повреждена (A), то взаимодействие личности с внешней средой нарушается (B). В этом случае (B) человек утрачивает реальное восприятие действительности (C), а значит (C), превращается в раба ситуации (D)». Это умозаключение имеет форму транзитивности импликации с тремя посылками:

.

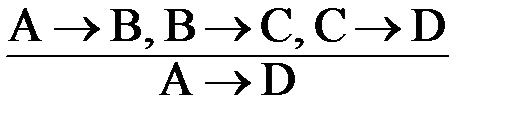Правило контрапозиции:

.

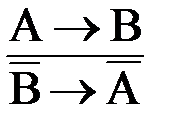Например: «Если человек знает геометрию (А), то он знает теорему Пифагора (В). Следовательно, если он не знает теоремы Пифагора (`В), то он не знает геометрии (`А)».

Все приведенные выше формы умозаключений являются правильными, т.е. их соблюдение гарантирует истинность заключения при истинности посылок. Иногда эти формы называют правилами соответствующих умозаключений.

Для проверки правильности умозаключений, не сводимых к этим формам, часто используется табличный метод. Чтобы его применить, нужно, прежде всего, составить формулу умозаключения: записать посылки и заключение на языке логики суждений (высказываний); соединить между собой посылки с помощью конъюнкции; присоединить заключение к посылкам с помощью импликации. Полученную таким образом формулу проверяют с помощью таблицы. Умозаключение будет правильным только в том случае, если его формула окажется тождественно истинной (в последнем столбце таблицы все значения – «истина»).

Например: «Если философ – дуалист, то он не материалист. Если он не материалист, то он диалектик или метафизик. Он не метафизик. Следовательно, он диалектик или дуалист».

Данное умозаключение довольно сложно привести к какому-либо стандартному типу, поэтому проверим его правильность табличным способом.

Запишем посылки и заключение нашего рассуждения на языке логики высказываний. Обозначим:

р – философ-дуалист;

q – философ-материалист;

r – философ-метафизик;

s – философ-диалектик.

Тогда первая посылка – «Если философ – дуалист (р), то он не материалист (ùq)» – на языке логики суждений имеет вид: рÉùq. Вторая посылка – «Если он не материалист (ùq), то он диалектик (s) или метафизик (r)» – запишется так: ùqÉsÚr. Третья посылка – «Он не метафизик: ùr. Заключение – «Он диалектик (s) или дуалист (р)»: sÚр.

Соединяя посылки конъюнкцией (Ù) и присоединяя к ним заключение импликацией (É), получаем формулу

[(р®ùq)Ù(ùq®sÚr)Ùùr]®(sÚр).

Таблица истинности для нее будет выглядеть так:

p

q

r

s

ùq

ùr

A

B

C

D

E

F

(р®ùq)

sÚr

ùq®B

AÙC

DÙùr

sÚр

D®F

И

И

И

И

Л

Л

Л

И

И

Л

Л

И

И

Л

И

И

И

Л

Л

И

И

И

И

Л

И

И

И

Л

И

И

И

Л

И

И

И

И

Л

И

И

Л

Л

И

И

И

Л

И

И

И

И

Л

И

И

И

И

Л

И

Л

И

Л

И

И

Л

Л

И

И

Л

И

Л

И

Л

И

И

И

И

И

И

И

И

И

Л

Л

И

И

И

И

И

И

И

И

И

И

Л

Л

Л

И

И

И

И

И

И

И

И

И

И

И

И

И

Л

Л

Л

Л

И

И

Л

Л

И

И

Л

И

И

Л

Л

Л

И

И

И

И

Л

Л

Л

И

Л

И

Л

И

Л

И

И

И

И

Л

И

И

Л

Л

И

Л

И

Л

И

И

И

И

Л

Л

Л

И

И

Л

Л

Л

И

Л

Л

И

Л

Л

И

И

Л

И

Л

Л

Л

И

И

Л

И

И

И

Л

Л

И

Л

Л

Л

И

И

И

Л

Л

Л

Л

И

И

Л

Л

Л

Л

И

И

И

Л

Л

Л

Л

Л

И

Так как последний столбец таблицы содержит и значения «истина», и значения «ложь», формула – выполнимая, что свидетельствует о вероятностном характере умозаключения.

Заметим, что при проверке правильности умозаключений, можно не строить таблицу полностью, а ограничиться рассмотрением только тех строк, в которых все посылки принимают значения «истина». Так, в данном примере, получив значения в столбцах 6 (третья посылка), 7 (первая посылка), 9 (вторая посылка) и 12 (заключение), достаточно исследовать только строки 6, 7, 8, 14.

Дело в том, что вести речь об истинности заключения имеет смысл исключительно при условии истинности посылок. При ложных посылках даже правильное по форме умозаключение не может гарантировать истинность заключения. Проверяя правильность умозаключения, по существу, проверяют, соблюдается ли в нем отношение дедуктивного логического следования. Если оно соблюдается, то во всех случаях, когда посылки – истинные суждения, заключение также окажется истинным суждением, и ни в одной строке таблицы не будет наблюдаться случая, когда все посылки истинны, а заключение ложно. При ложной же посылке вообще нельзя говорить об отношении логического следования.