Воспроизведение арифметических операций и произвольных функциональных зависимостей

В цифровых устройствах часто воспроизводятся различные функциональные зависимости, заданные аналитически или таблично.

Для функций одного аргумента (тригонометрических, логарифмических и др.) объем памяти таблиц легко вычислить, зная разрядность аргумента и функции.

Пусть аргумент задается 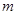разрядным словом, тогда число точек, в которых задана функция составит 2^m.

Если разрядность выходного слова, которым представляется значение функции равна 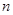, то очевидно емкость памяти в битах .

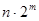Если принять 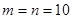(точность ~0,1%), то объем памяти 10К (реализуется на одном кристалле).

С ростом числа аргументов функции объем памяти таблиц быстро растет.

Чисто табличный метод решения задачи становится неприемлемым.

В этих случаях полезно рассмотреть таблично-алгоритмические методы решения, в рамках которых введя наибольшее число простых операций над данными можно существенно снизить объем таблиц.

При использовании таблично-алгоритмического метода запоминаются лишь некоторые (узловые) значения функций, промежуточные вычисляются по несложным алгоритмам.

А ´ В 8 ´ 8 – произведение имеет разрядность 16.

Объем памяти для чисто табличного метода: 2^2*8 * 16 = 2²⁰ бит.

Для перехода к таблично-алгоритмическому методу решения: рассматриваем сомножители как суммы двух частей – старшей и младшей.

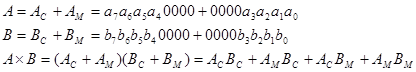
Объем памяти для хранения результата перемножения четырех четырехразрядных операндов 2^2*4 * 8 = 2048 бит. Затрачиваемый на четыре перемножения общий объем памяти 4 ´ 2048 = 8К бит, что в 128 раз меньше, чем для чисто табличного перемножителя.

При воспроизведении функций 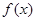простейший таблично-алгоритмический метод – кусочно-линейная аппроксимация.

Запоминаются узловые значения функции в промежутках между узлами функция вычисляется по простому алгоритму в предположении, что на этих промежутках функция изменяется линейно. Число узлов выбирается по соображениям точности линейной аппроксимации.

Кусочно-линейной аппроксимации с постоянным шагом соответствуют следующие представления аргумента и функции:

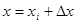
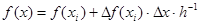
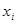- координата i узловой точки.

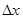- разность значений х и координаты ближайшей слева узловой точки;

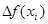- приращение функции на промежутке от 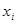до ;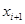

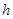- шаг аппроксимации.

Структура функционального преобразователя с кусочно-линейной аппроксимацией:

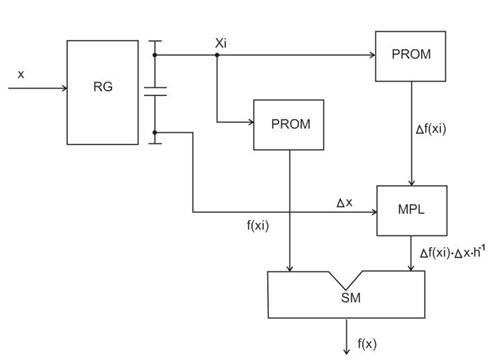
Емкость памяти при переходе от табличного метода к таблично-алгоритмическому существенно сокращается, и быстродействие остается высоким, так как современная элементная база содержит быстродействующие перемножители и сумматоры.