Прямые измерения с многократными наблюдениями
При статистической обработке результатов наблюдений по ГОСТу 8.207-76 выполняют следующие операции.
1. Исключают известные систематические погрешности из результатов наблюдений.
2. Вычисляют среднее арифметическое исправленных результатов наблюдений, которое принимают за результат измерения. Вычисления проводят по формуле
,
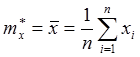где x1, x2…xn - совокупность наблюдаемых значений случайной величины X.
Среднее арифметическое результатов наблюдений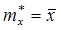 
является несмещенной оценкой для генерального среднего нормального распределения.
3. Определяют наличие грубых погрешностей (промахов), если закон распределения вероятностей нормальный, то их исключают из рассмотрения и повторяют вычисления с оставшейся новой совокупностью результатов наблюдения.
4. Вычисляют оценку среднеквадратического отклонения результата наблюдения. Несмещённую оценку для СКО определяют по формуле:
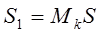
5. Вычисляют оценку среднеквадратического и средне-арифметического отклонений:
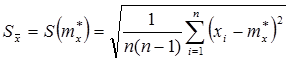
6. Проверяют гипотезу о том, что результаты наблюдений принадлежат нормальному распределению.
7. Вычисляют доверительные границы случайных погрешностей при доверительной вероятности p=0,95, если результаты измерения в дальнейшем повторить нельзя p=0,99.
8. Определяют границы неисключенной систематической погрешности результатов измерения.
9. Вычисляют доверительные границы погрешности результата. Если выполняется условие
,
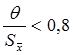то неисключенной систематической погрешностью можно пренебречь и определить доверительные границы погрешности результата, как доверительные границы случайной погрешности
,
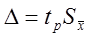при p=0,95 (и p=0,99) ; если же выполняется условие: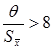 
,то можно пренебречь случайной погрешностью и тогда: 
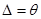при p=0,95 (p=0,99).
В случае, если эти условия не выполняются, то доверительные границы погрешности результата определяются по формуле: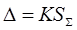 
,где коэффициент K, зависящий от соотношения случайной и неисключенной систематической погрешностей, находят из выражения:
,
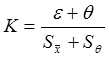а среднеквадратическое отклонение общей погрешности результата измерения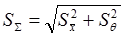 
находят квадратическим суммированием дисперсии случайной 
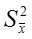и среднеквадратическим отклонением систематической погрешности 
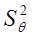результата измерения.
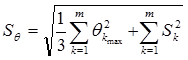
Примечание: коэффициент 1/3 получается из-за того, что распределение систематических погрешностей равномерное.
10. Результат измерения записывают в виде: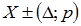 
, а при отсутствии сведений - в виде функции распределения составляющих погрешности и необходимости дальнейшей обработки результатов и анализа погрешностей в виде: 
.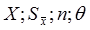