Краткие теоретические сведения. Сложные суждения (высказывания) могут комбинироваться друг с другом, образуя сложные логические формулы.
Сложные суждения (высказывания) могут комбинироваться друг с другом, образуя сложные логические формулы.
Логическая формула содержит следующие элементы:
1) логические переменные, обозначаемые A, B, C, D… (a, b, c, d…);
2) логические постоянные, или логические связки, обозначаемые 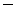 ,
, 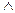 ,
, 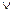 ,
, 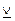 , →, ↔;
, →, ↔;
3) скобки ( ).
Формулы логики высказываний бывают трех видов:
1) тождественно-истинная формула (закон логики, тавтология), которая принимает только логическое значение «истина» для любого набора логических значений входящих в нее переменных;
2) тождественно-ложная формула (логическое противоречие), которая принимает только значение «ложь» для любого набора логических значений входящих в нее переменных;
3) нейтральная формула, которая принимает как значение «истина», так и значение «ложь».
Рассуждение называется правильным, если его логическая формула есть закон логики, то есть тождественно-истин-ная. В противном случае рассуждение является неправильным. Для проверки правильности рассуждений используют, например, таблицы истинности логических формул. Следует помнить, что число строк таблицы истинности определяется формулой 2n, где n – число переменных в формуле. В случае, когда в логическую формулу входит более 4-х переменных, более рациональным является сокращенный способ проверки (посредством допущения).
Пример 1.Запишите логическую формулу высказываний, определите их логическое значение.
а) Две прямые a и b параллельны тогда и только тогда, когда эти прямые лежат в одной плоскости и не пересекаются или совпадают.
б) Неверно, что учащийся знает арифметику или знает геометрию, тогда и только тогда, когда он не знает ни арифметику, ни геометрию.
в) Соли, которые не окрашены, это соли, которые не являются органическими соединениями, или это органические соединения, которые не окрашены.
Решение:
а) данное сложное высказывание состоит из четырех простых: А–прямые a и b параллельны, В – прямые a и b лежат в одной плоскости, С –прямые a и b пересекаются, D–прямые a и b совпадают. Используя обозначения логических союзов, получим логическую формулу данного сложного высказывания:
А ↔ (В 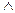 (
( 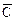
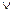 D));
D));
б) данное сложное высказывание состоит из двух простых: А – учащийся знает арифметику, В – учащийся знает геометрию. Логическая формула имеет вид:
( 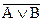 )↔(
)↔( 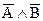 );
);
в) данное сложное высказывание состоит из трех простых: А – некоторое вещество есть соль, В – некоторое вещество есть органическое соединение, С – некоторое вещество окрашено. Тогда, используя обозначения соответствующих логических союзов, получим:
(А 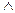
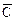 ) → ((А
) → ((А 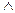
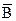 )
) 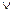 (В
(В 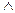
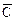 )).
)).
Пример 2. Табличным способом определите вид логической формулы высказывания:
а) А → (А 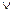 В);
В);
б) ( 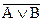 )
) 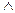 (
( 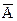
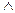 В);
В);
в) А → ((В 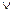 С) → (С →
С) → (С → 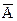 )).
)).
Решение:
а) Формула содержит две переменные, значит таблица истинности имеет четыре строки логических значений:
| А | В | А 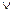 В В | А 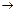 (А (А 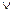 В) В) |
| И | И | И | И |
| И | Л | И | И |
| Л | И | И | И |
| Л | Л | Л | И |
Поскольку на выходе логической формулы (в последнем столбце таблицы истинности) имеется только значение «истина», то данная формула тождественно-истинная, или закон логики;
б) аналогично предыдущему пункту построим таблицу истинности формулы:
| А | В | 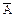 | 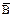 | А 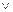 В В | 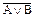 | 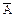 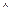 В В | ( 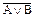 ) ) 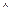 ( ( 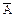 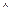 В) В) |
| И | И | Л | Л | И | Л | Л | Л |
| И | Л | Л | И | И | Л | Л | Л |
| Л | И | И | Л | И | Л | И | Л |
| Л | Л | И | И | Л | И | Л | Л |
Поскольку на выходе логической формулы имеется только значение «ложь», формула является тождественно-ложной, или логическим противоречием;
в) формула содержит три переменные, значит таблица истинности имеет восемь строк логических значений:
| А | В | С | 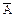 | В 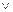 С С | С 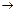 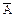 | (В 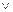 С) С) 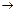 (С (С 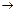 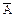 ) ) | А 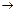 ((В ((В 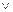 С) С) 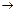 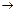 (С (С 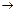 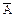 )) )) |
| И | И | И | Л | И | Л | Л | Л |
| И | И | Л | Л | И | И | И | И |
| И | Л | И | Л | И | Л | Л | Л |
| Л | И | И | И | И | И | И | И |
| И | Л | Л | Л | Л | И | И | И |
| Л | И | Л | И | И | И | И | И |
| Л | Л | И | И | И | И | И | И |
| Л | Л | Л | И | Л | И | И | И |
Поскольку на выходе логической формулы имеется как значение «истина», так и «ложь», формула является нейтральной.
Пример 3.Проверьте правильность рассуждения табличным способом.
Если число а делится на 2 и на 3, то оно делится на 6. Число а неделится на 6, но делится на 3. Значит, а не делится на 2.
Решение:
высказывание состоит из трех простых суждений: А – число а делится на 2, В – число а делится на 3, С – число а делится на 6. Логическая формула рассуждения имеет вид:
(((А 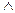 В)
В) 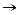 С)
С) 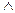 (
( 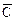
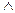 В))
В)) 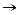

Составим таблицу истинности формулы и определим, является ли она тождественно-истинной.
| А | В | С | 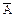 | 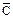 | А 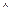 В В | 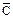 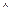 В В | (А 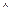 В) → → С В) → → С | ((А 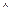 В)→С) В)→С) 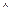 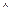 ( ( 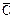 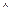 В) В) | (((А 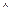 В)→→С) В)→→С) 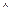 ( ( 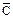 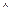 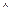 В)) → В)) → 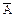 | |
| И | И | И | Л | Л | И | Л | И | Л | И | |
| И | И | Л | Л | И | И | И | Л | Л | И | |
| И | Л | И | Л | Л | Л | Л | И | Л | И | |
| Л | И | И | И | Л | Л | Л | И | Л | И | |
| И | Л | Л | Л | И | Л | Л | И | Л | И | |
| Л | И | Л | И | И | Л | И | И | И | И | |
| Л | Л | И | И | Л | Л | Л | И | Л | И | |
| Л | Л | Л | И | И | Л | Л | И | Л | И |
Поскольку формула является тождественно-истинной, то рассуждение, проводимое в соответствии с ней, является правильным.
Пример 4.Проверьте правильность рассуждения сокращенным способом.
В бюджете возникнет дефицит, если не повысят пошлины. Если в бюджете будет дефицит, то государственные расходы на общественные нужды придется сократить. Значит, если повысят пошлины, то государственные расходы на общественные нужды не сократятся.
Решение:
запишем логическую формулу рассуждения, обозначив: А – в бюджете возникнет дефицит, В – пошлины повысят, С – государственные расходы на общественные нужды сократятся. Получим:
(( 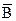
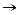 А)
А) 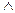 (А
(А 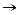 С))
С)) 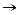 (В
(В 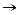
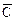 ).
).
Проверим, является ли формула тождественно-истинной сокращенным способом – методом допущений. Допустим, что формула принимает, по крайней мере, одно значение «ложь». Поскольку последняя логическая операция в формуле – это имп-ликация, то она ложна только в одном случае: когда основание истинно, а следствие ложно, то есть ( 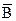
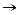 А)
А) 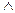 (А
(А 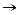 С) принимает значение «истина», В
С) принимает значение «истина», В 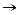
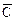 принимает значение «ложь».
принимает значение «ложь».
Рассмотрим вначале импликацию В 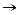
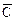 . Так как импликация ложна только в одном случае, значит В – «истина»,
. Так как импликация ложна только в одном случае, значит В – «истина», 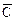 – «ложь», а С – «истина».
– «ложь», а С – «истина».
Далее, так как конъюнкция истинна только в одном случае, значит 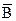
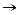 А – «истина», А
А – «истина», А 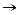 С – «истина».
С – «истина».
Каждая из этих формул не содержит противоречия.
Если 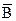 – «ложь» (согласно установленному выше), и А – «истина» либо «ложь», то (
– «ложь» (согласно установленному выше), и А – «истина» либо «ложь», то ( 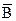
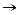 А) – «истина».
А) – «истина».
Если А – «истина» либо «ложь», и С – «истина» (согласно установленному выше), то (А 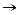 С) – «истина».
С) – «истина».
Так как, рассуждая, в итоге, мы не пришли к противоречию в целом, то первоначальное допущение верно, формула принимает одно значение «ложь», то есть не является тождественно-истинной.
Рассуждение является неправильным.
Практическая часть
Вариант 1
Задание 1. В заданных сложных высказываниях выделите простые, запишите их символически, определите значение истинности сложных высказываний, поясните выбор.
а) Отрезок, треугольник, круг – плоские фигуры.
б) Число 396 кратное 2-м и 3-м, кратно 6.
в) 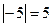 или
или 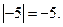
г) Число 19 – составное и четное.
Задание 2. Пусть даны высказывания:
А: 3 – однозначное число,
В: 3 – нечетное число,
С: 3 – простое число.
Сформулируйте из них словесно сложное высказывание: А 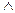 В
В 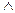 С, определите его истинностное значение.
С, определите его истинностное значение.
Задание 3. Составив таблицу истинности, выясните, является ли следующая формула законом логики (тавтологией): 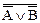
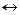
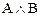 .
.
Задание4. Проверьте табличным или сокращенным способом правильность рассуждения.
Если правильно внести удобрения, то урожай повысится. Если урожай повысится, то себестоимость продукции станет ниже. Значит, если правильно внести удобрения, то себестоимость продукции станет ниже.
Вариант 2
Задание 1. В заданных сложных высказываниях выделите простые, запишите их символически, определите значение истинности высказываний, поясните выбор.
а) 3 – не является простым числом.
б) Элементы, принадлежащие двум множествам одновременно, принадлежат их пересечению.
в) 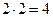 , и
, и 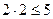 , и
, и 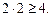
г) Если 18 делится на 6, то оно делится на 3 и на 2.
Задание 2. Пусть дано истинное высказывание
В:В треугольнике АВС медиана является высотой.
Сформулируйте словесно сложное высказывание 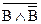 , определите его истинностное значение.
, определите его истинностное значение.
Задание 3. Составив таблицу истинности, выясните, является ли следующая формула законом логики (тавтологией): 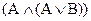
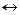
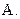
Задание4.Проверьте табличным или сокращенным способом правильность рассуждения.
Если бензин не подорожает, то уберем урожай, и если бензин подорожает, то уберем урожай. Следовательно, уберем урожай.
Вариант 3
Задание 1. В заданных сложных высказываниях выделите простые, запишите их символически, определите значение истинности высказываний, поясните выбор.
а) Если 10 делится на 3, то 3 меньше 10.
б) Два множества Аи В пересекаются, или не пересекаются, или равны.
в) Число 5407 делится на 9 тогда и только тогда, когда сумма 5 + 4 + 0 + 7 делится на 9.
г) 7 – простое число, и 9 – простое число.
Задание 2. Пусть даны высказывания:
А: Число 3 лежит между 5 и 7.
В: Число 3 больше 5.
С: Число 3 меньше 7.
Сформулируйте из них словесно сложное высказывание: А 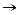 (В
(В 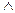 С), определите его истинностное значение.
С), определите его истинностное значение.
Задание 3. Составив таблицу истинности, выясните, является ли следующая формула законом логики (тавтологией):
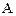
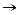
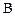
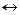
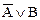 .
.
Задание 4. Проверьте табличным или сокращенным способом правильность рассуждения.
Водоемы бывают пресные или соленые. Это озеро – прес-ный водоем. Значит, это озеро не является соленым водоемом.
Вариант 4
Задание 1. В заданных сложных высказываниях выделите простые, запишите их символически, определите значение истинности высказываний, поясните выбор.
а) Число 19 простое и нечетное.
б) Произведение трех чисел а, b, с равно 0 тогда и только тогда, когда одно из них равно 0.
в) Всякое действительное число является натуральным.
г) Если число 241 нечетное, то оно делится на 3.
Задание 2. Пусть дано истинное высказывание
А: В треугольнике АВС медиана является биссектрисой.
Сформулируйте словесно высказывание 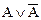 , определите его истинностное значение.
, определите его истинностное значение.
Задание 3. Составив таблицу истинности, выясните, является ли следующая формула законом логики (тавтологией):
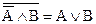 .
.
Задание 4.Проверьте табличным или сокращенным способом правильность рассуждения.
Если весна наступила, то в фермерском хозяйстве предстоит много работ. Весна не наступила. Значит, в фермерском хозяйстве не предстоит много работ.
Вариант 5
Задание 1.В заданных сложных высказываниях выделите простые, запишите их символически, определите значение истинности высказываний, поясните выбор.
а) Если сумма 3 + 4 + 2 делится на 9, то число 342 делится на 9.
б) Число 275 простое и делится на 5, или число 275 составное и делится на 5.
в) 2 – число четное и простое.
г) Четырехугольник, имеющий две оси симметрии, есть ромб.
Задание 2. Пусть даны высказывания:
А: 10 делится на 5.
В: 10 – двузначное число.
С: 10 – простое число.
Сформулируйте словесно высказывание: А 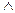 (В
(В 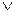 C), определите его истинностное значение.
C), определите его истинностное значение.
Задание 3. Составив таблицу истинности, выясните, является ли следующая формула законом логики (тавтологией):
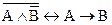 .
.
Задание 4. Проверьте табличным или сокращенным способом правильность рассуждения.
Если магнит нагреть, то он размагнитится. Магнит размагнитился. Значит, магнит нагрели.
Вариант 6
Задание 1. В заданных сложных высказываниях выделите простые, запишите их символически, определите значение истинности высказываний, поясните выбор.
а) Числа –3, –2, –1 являются целыми и удовлетворяют неравенству 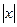 < 4.
< 4.
б) Два множества, состоящие из одинаковых элементов, равны.
в) Если делимое равно делителю, то их частное равно 1 и остаток равен 0.
г) Всякое натуральное число является действительным.
Задание 2. Пусть даны высказывания
А: 5 – ненатуральное число.
В: 5 – отрицательное число.
С: 5 – дробное число.
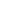
 Сформулируйте из них словесно сложное высказывание: А
Сформулируйте из них словесно сложное высказывание: А 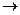 (В
(В 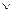 C), определите его истинностное значение.
C), определите его истинностное значение.
Задание 3. Составив таблицу истинности, выясните, является ли следующая формула законом логики (тавтологией):
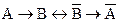 .
.
Задание 4. Проверьте табличным или сокращенным способом правильность рассуждения.
Если он – автор этого слуха, то он беспринципен или глуп. Но он не глуп и не лишен принципов. Значит, не он – автор этого слуха.
Вариант 7
Задание 1. В заданных сложных высказываниях выделите простые, запишите их символически, определите значение истинности высказываний, поясните выбор.
а) Число 179 положительное и делится на 9, или число 179 положительное и не делится на 9.
б) Число 21 простое и нечетное.
в) 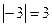 и
и 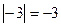 .
.
г) Если одно двузначное число больше другого двузначного числа, то число десятков первого числа больше числа десятков второго числа или число десятков у них одинаковое, а число единиц первого числа больше числа единиц второго числа.
Задание 2. Пусть даны истинные высказывания:
А: В треугольнике АВС медиана является биссектрисой.
В:В треугольнике АВС медиана является высотой.
Сформулируйте из них словесно сложное высказывание: 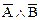 , определите его истинностное значение.
, определите его истинностное значение.
Задание 3. Составив таблицу истинности, выясните, является ли следующая формула законом логики (тавтологией):
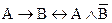 .
.
Задание 4. Проверьте табличным или сокращенным способом правильность рассуждений.
Если данное тело графит, то оно электропроводно. Данное тело электропроводно. Значит, данное тело – графит.
Вариант 8
Задание 1. В заданных сложных высказываниях выделите простые, запишите их символически, определите значение истинности высказываний, поясните выбор.
а) Число, меньшее 10, однозначное.
б) Число 225 делится на 45 тогда и только тогда, когда оно делится на 5 и на 9.
в) Равносторонний треугольник является остроугольным, или тупоугольным, или прямоугольным.
г) Если 241 делится на 9, то 241 делится на 3.
Задание 2. Пусть даны высказывания:
А: 138 – натуральное число.
В: 138 делится без остатка на 3.
С: 138 – составное число.
Сформулируйте из них словесно сложное высказывание: (А 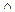 В) → С, определите его истинностное значение.
В) → С, определите его истинностное значение.
Задание 3. Составив таблицу истинности, выясните, является ли следующая формула законом логики (тавтологией):
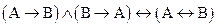 .
.
Задание 4.Проверьте табличным или сокращенным способом правильность рассуждения.
Если бухта замерзла, то суда не могут входить в бухту. Суда не могут входить в бухту. Значит, бухта замерзла.
Вариант 9
Задание 1. В заданных сложных высказываниях выделите простые, запишите их символически, определите значение истинности высказываний, поясните выбор.
а) 7 – простое число или 9 – простое число.
б) Дизъюнкция двух высказываний истинна, если истинно хотя бы одно из данных высказываний.
в) Число 17 больше числа 14 тогда и только тогда, когда найдется такое число 3, что 14 + 3 = 17.
г) Если число 7 предшествует 8 в натуральном ряду, то 7 < 8.
Задание 2. Пусть даны истинные высказывания:
А: В треугольнике АВС медиана является биссектрисой.
В:В треугольнике АВС медиана является высотой.
Сформулируйте из них словесно сложное высказывание 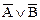 , определите его истинностное значение.
, определите его истинностное значение.
Задание 3. Составив таблицу истинности, выясните, является ли следующая формула законом логики (тавтологией):
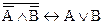 .
.
Задание 4. Проверьте табличным или сокращенным способом правильность рассуждения.
Если река выходит из берегов, то вода заливает прилежащие территории. Вода реки не залила прилежащих территорий. Значит, река не вышла из берегов.
Вариант 10
Задание 1. В заданных сложных высказываниях выделите простые, запишите их символически, определите значение истинности высказываний, поясните выбор.
а) Частное, в котором делимое равно нулю, также равно нулю.
б) Трапеция – четырехугольник или пятиугольник.
в) Число 124 трехзначное тогда и только тогда, когда оно состоит из трех цифр.
г) Число, делящееся на 5 и 7, делится на 35.
Задание 2. Пусть даны истинные высказывания:
А: В треугольнике АВС медиана является биссектрисой.
В:В треугольнике АВС медиана является высотой.
Сформулируйте из них словесно сложное высказывание 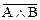 , определите его истинностное значение.
, определите его истинностное значение.
Задание 3. Составив таблицу истинности, выясните, является ли следующая формула законом логики (тавтологией):
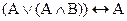 .
.
Задание 4.Проверьте табличным или сокращенным способом правильность рассуждения.
Учащиеся в контрольной работе по программированию допускают вычислительные или содержательные ошибки. Учащийся Коровьев допустил в контрольной работе вычислительные ошибки. Значит, Коровьев не допустил в контрольной работе содержательных ошибок.
Контрольные вопросы
1. Что называют высказыванием?
2. Назовите виды высказываний.
3. Охарактеризуйте виды формул логики высказываний.
4. Перечислите логические союзы, укажите их истинностные значения.
5. Назовите логические отношения между совместимыми высказываниями.
6. Перечислите логические отношения между несовместимыми высказываниями.
7. Что такое табличный метод проверки рассуждений?
8. В чем сущность сокращенного метода проверки правильности рассуждений?
9. Назовите основные логические законы.
10. Какова роль законов логики в познании?
Категорический силлогизм
Цель работы: закрепить практические навыки умозаключения посредствомкатегорического силлогизма; научиться анализировать корректность умозаключений; выработать навыки восстановления сокращенных силлогизмов.
