Дискретные аппроксимации

Рассмотрим группу элементов изображения размером 2x2:

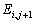
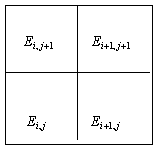
Производные в центральной точке этой группы можно оценить следующим образом:

,

,

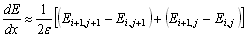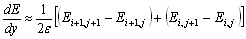где 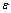— расстояние между центрами соседних элементов. Каждая оценка представляет собой среднее двух конечно-разностных приближений.

Конечно-разностная аппроксимация производной всегда относится к определенной точке. Так, обычная конечно-разностная формула дает оценку, которая является несмещенной по отношению к точке, расположенной посередине между точками отсчета оцениваемой функции. Формулы, приведенные выше для оценки частных производных, выбраны именно такими потому, что они не смещены относительно одной и той же точки, а именно относительно общей угловой вершины в центре четырех рассматриваемых элементов изображения (пикселов). Теперь квадрат градиента можно аппроксимировать следующим образом:

.

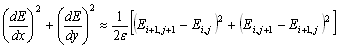Если выполнить эти простые вычисления для всего изображения, то мы получим большие значения в тех местах, где яркость изменяется быстро. В областях постоянной яркости выход равен нулю. (Если присутствует шум, то выход отличен от нуля, но достаточно мал.) Результаты такой обработки можно занести в новый массив изображения, в котором края уже будут значительно усилены.

Аналогично рассматривают группу элементов размером 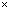3 3.