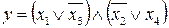Высказывания и логические операции
Логические основы информатики
Алгебра логики (алгебра высказываний) и основы математической логики играют важную роль в информатике. Математическая логика присутствует в различных разделах информатики в виде:
1) двоичной логики, на которой основана работа цифровых компьютеров;
2) специальной алгебры логики, лежащей в основе математической модели реляционных баз данных;
3) правил, определяющих функционирование алгоритмов и программ, работу интеллектуальных и экспертных систем.
Высказывания и логические операции
Основным понятием математической логики является понятие простого высказывания.
Высказывание – это повествовательное предложение, утверждающее что-либо о чем-либо, о котором можно сказать, истинно оно или ложно в данных условиях. Логическими значениями высказываний являются «истина» и «ложь».
В алгебре логики все высказывания рассматриваются только с точки зрения их логического значения. Каждое высказывание либо истинно, либо ложно, и ни одно высказывание не может быть одновременно истинным и ложным.
Пример. Рязань – столица РФ. Значение высказывания – «ложь».
Москва – столица РФ. Значение высказывания «истина».
Высказывание, представляющее собой одно утверждение, принято называть простым, или элементарным.
Высказывания, которые получаются из элементарных с помощью грамматических связок «не», «и», «или», «если», «то», «тогда и только тогда», принято называть сложными, или составными.
Пример. Карась не рыба. Значение высказывания – «ложь».
Элементарные высказывания обозначаются малыми буквами латинского алфавита; истинное значение высказывания цифрой 1, а ложное значение — цифрой 0. Например, если высказывание x истинно, то будет справедлива запись x = 1, если высказывание x ложно, то x = 0.
При изучении логики высказываний предполагается, что все простые высказывания, входящие в рассмотрение, обладают одним из двух свойств — являются истинными либо ложными. Поэтому и само высказывание может быть истинно или ложно.
Над высказываниями можно выполнять логические операции:
1) отрицание;
2) конъюнкция;
3) дизъюнкция;
4) импликация;
5) эквивалентность и др.
Операция отрицания высказывания х обозначается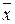 
и читается «не х» или «неверно, что х».
Отрицание высказывания – это новое высказывание, которое является истинным, если высказывание x ложно, и ложным, если высказывание x истинно.
Таблица 1 – Таблица истинности логической операции НЕ (инверсия, отрицание)
| Аргумент | Результат |
| x |  |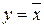
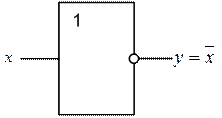
Рисунок 1 – Инвертор
Пример. Ока впадает в Волгу. Значение – «истина».
Ока не впадает в Волгу. Значение – «ложь».
Операция конъюнкции высказываний 
и 
обозначается символом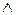 
, а выражение 
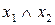читается « 
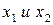». Высказывания и называются членами конъюнкции.
Конъюнкция (логическое умножение) высказываний – это новое высказывание, которое считается истинным, если все высказывания, входящие в конъюнкцию истинны, и ложным, если хотя бы одно из высказываний ложно.
Таблица 2 – Таблица истинности логической операции И
| Аргумент | Результат | |
| | |  |
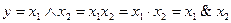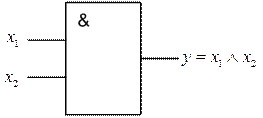
Рисунок 2 – Конъюнктор
Пример. Пусть x1: Ока впадает в Волгу. Значение – «истина».
x2: Рязань – столица РФ. Значение – «ложь».
Тогда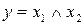 
примет значение «ложь».
Операция дизъюнкции высказываний и обозначается символом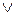 
, а выражение 
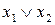читается как « 
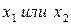». Высказывания и называются членами дизъюнкции.
Дизъюнкция (логическое сложение) высказываний – это высказывание, которое считается истинным, если хотя бы одно из высказываний, входящих в дизъюнкцию истинно. Результатом дизъюнкции будет ложь, если ложны все высказывания, входящие в дизъюнкцию.
Таблица 3 – Таблица истинности логической операции ИЛИ
| Аргумент | Результат | |
| | |  |
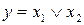Рисунок 3 – Дизъюнктор
Пример. Пусть x1: Ока впадает в Волгу. Значение – «истина».
x2: Рязань – столица РФ. Значение – «ложь».
Тогда 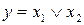примет значение «истина».
Операции И, ИЛИ, НЕ образуют булевый (логический) базис. Базис – это такой набор логических функций, с помощью которого можно построить любую сколь угодно сложную логическую функцию.
Таблица 4 – Таблица истинности логической операции И-НЕ (отрицание конъюнкции, штрих Шеффера)
| Аргумент | Результат | |
| | |  |
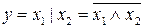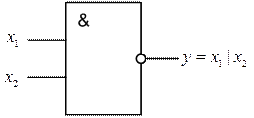
Рисунок 5 – Элемент И-НЕ (элемент Шеффера)
Операция И-НЕ образует базис Шеффера.
Таблица 5 – Таблица истинности логической операции ИЛИ-НЕ (отрицание дизъюнкции, стрелка Пирса)
| Аргумент | Результат | |
| | |  |
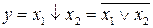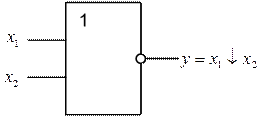
Рисунок 6 – Элемент ИЛИ-НЕ (элемент Пирса)
Операция ИЛИ-НЕ образует базис Пирса.
Операция импликации высказываний и обозначается символом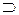 
, а выражение 
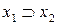читается как «если х, то у». Высказывание называют условием, или посылкой, высказывание — следствием, или заключением, а высказывание 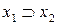— следованием, или импликацией.
Импликация двух высказываний и – это новое высказывание, которое считается ложным, если – истинно, а – ложно, и истинным во всех остальных случаях.
Таблица 6 – Таблица истинности логической операции ИМПЛИКАЦИЯ
| Аргумент | Результат | |
| | |  |
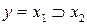Пример. Пусть x1: Число 12 делится на 6. Значение – «истина».
x2: Число 12 делится на 3. Значение – «истина».
Тогда 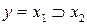отражает высказывание «Если число 12 делится на 6, то оно делится на 3» и является истинным.
Операция эквивалентности высказываний и обозначается символом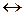 
, а выражение 
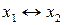читается «для того чтобы , необходимо и достаточно, чтобы » или « тогда и только тогда, когда ». Высказывания и называются членами эквивалентности.
Эквивалентность двух высказываний и – это новое высказывание, которое считается истинным, если оба высказывания либо одновременно истинны, либо одновременно ложны, и ложным во всех остальных случаях.
Таблица 7 – Таблица истинности логической операции ЭКВИВАЛЕНТНОСТЬ
| Аргумент | Результат | |
| | |  |
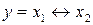Пример. Высказывание : «Треугольник SPQ с вершиной S и основанием PQ – равнобедренный», высказывание : «В треугольнике SPQ с вершиной S и основанием PQ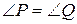 
», можно записать высказывание «Треугольник SPQ с вершиной S и основанием PQ равнобедренный тогда и только тогда, когда 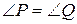» в форме эквивалентности 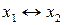. Эквивалентность является истинной, так как высказывания либо одновременно истинны, либо одновременно ложны.
Алгебра логики
Формула алгебры логики – это сложное высказывание, которое может быть получено из элементарных высказываний посредством применения логических операций отрицания, конъюнкции, дизъюнкции, импликации и эквивалентности.
Пример.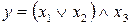 
.
Правила записи формулы.
1. Скобки можно опускать, придерживаясь следующего порядка действий:
а) конъюнкция выполняется раньше, чем остальные операции;
б) дизъюнкция выполняется раньше, чем импликация и эквивалентность.
2. Если над формулой стоит знак отрицания, то скобки опускаются.
3. Количество открывающих скобок должно быть равно количеству закрывающих.
Логическое значение формулы алгебры логики полностью определяется результатом логических операций над значениями входящих в нее элементарных высказываний.
Таблица истинности позволяет полностью описать все возможные значения любой формулы в зависимости от значений входящих в нее элементарных высказываний.
Таблица 8 – Таблица истинности высказывания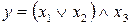
| Аргументы | Результат | |||
| | |  |  | |
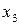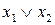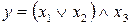Основные равносильности
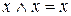
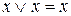
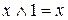
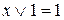
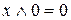
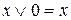
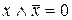- закон противоречия
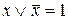- закон исключения третьего
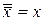- закон снятия двойного отрицания
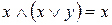
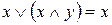
Задача 2. Дано выражение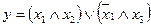 
Таблица истинности высказывания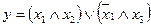
| Аргументы | Результат | ||||||
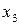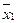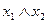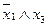| | | |  |  |  | y | |
Схема.
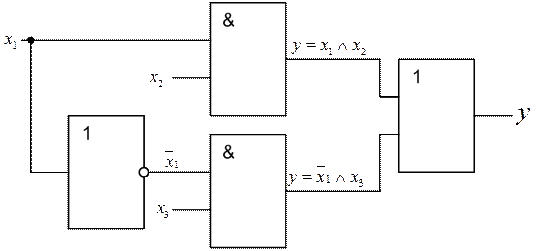
Рисунок 7 – Логическая схема для выражения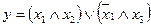
Задача 3. Дано выражение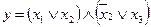 
Таблица истинности высказывания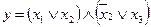
| Аргументы | Результат | ||||||
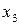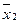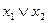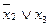| | | |  |  |  | y | |
Схема.
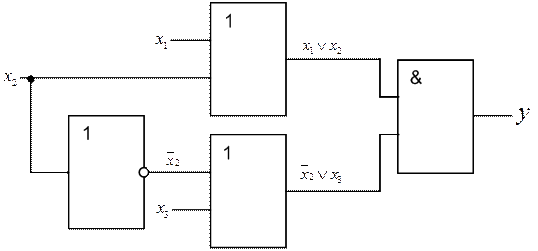
Рисунок 8 – Логическая схема для выражения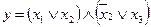
Задача 4. Дано выражение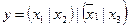 
Таблица истинности высказывания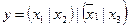
| Аргументы | Результат | ||||||
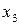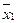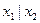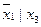| | | | |  |  | y | |
Схема.
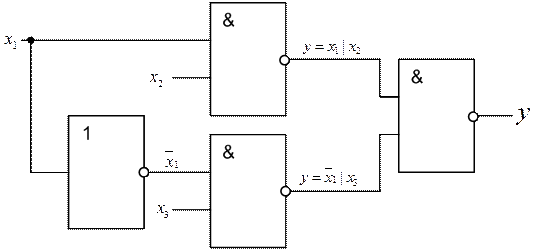
Рисунок 9 – Логическая схема для выражения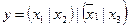
Операцию инверсии можно реализовать с помощью элементов И-НЕ.
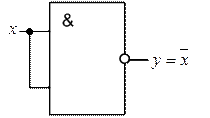
Рисунок 10 – Реализация операции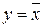 
на основе элемента И-НЕ
Схема (см. рисунок 9), построенная на основе однотипных элементов, примет следующий вид (рисунок 11).
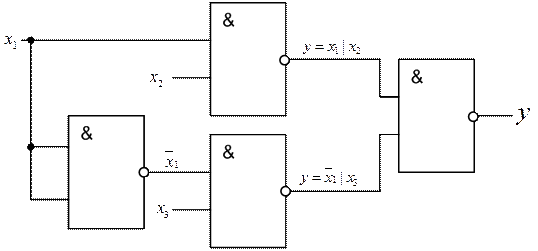
Рисунок 11 – Логическая схема для выражения 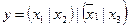, состоящая из однотипных элементов
Задача 5. Дано выражение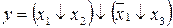 
Таблица истинности высказывания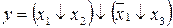
| Аргументы | Результат | ||||||
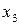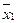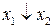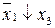| | | | |  |  | y | |
Схема.
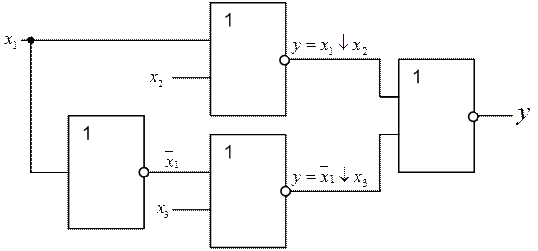
Рисунок 12 – Логическая схема для выражения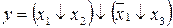
Задания на самостоятельную работу.
Задача 1. Построить таблицу истинности и логическую схему.
1. 
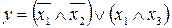
2. 
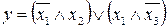
3. 
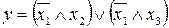
4. 
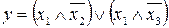
5. 
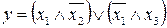
6. 
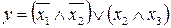
7. 
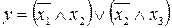
8. 
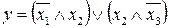
9. 
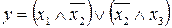
10. 
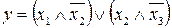
11. 
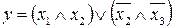
12. 
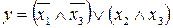
13. 
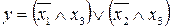
14. 
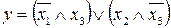
15. 
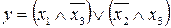
16. 
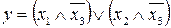
17. 
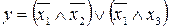
18. 
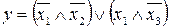
19. 
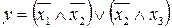
20. 
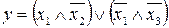
21.
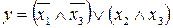
22.
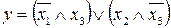
23.
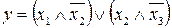
24.
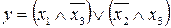
25.
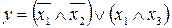
26.
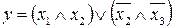
27.
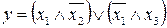
28.
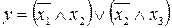
29.
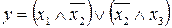
30.
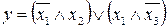
31.
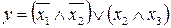
32.
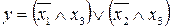
33.
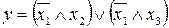
34.
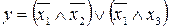
35.
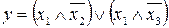
36.
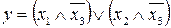
37.
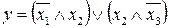
38.
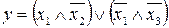
Задача 2. Построить таблицу истинности и логическую схему.
1. 
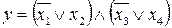
2. 
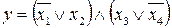
3. 
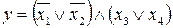
4. 
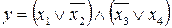
5. 
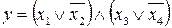
6. 
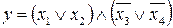
7. 
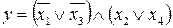
8. 
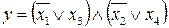
9. 
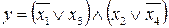
10. 
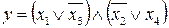
11. 
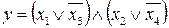
12. 
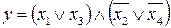
13. 
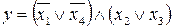
14. 
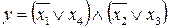
15. 
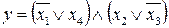
16. 
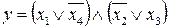
17. 
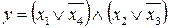
18. 
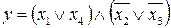
19. 
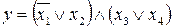
20. 
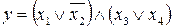
21. 
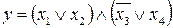
22. 
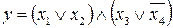
23. 
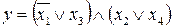
24. 
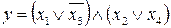
25. 
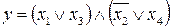
26. 
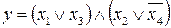
27. 
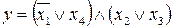
28. 
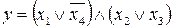
29. 
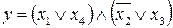
30. 
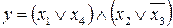
31. 
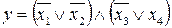
32. 
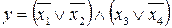
33. 
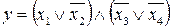
34. 
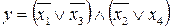
35. 
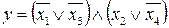
36. 
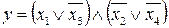
37. 
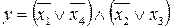
38. 
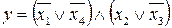
Задача 3. Построить таблицу истинности и логическую схему.
1. 
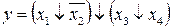
2. 
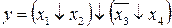
3. 
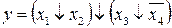
4. 
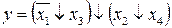
5. 
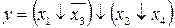
6. 
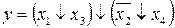
7. 
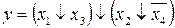
8. 
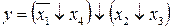
9. 
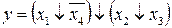
10. 
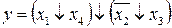
11. 
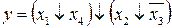
12. 
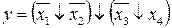
13. 
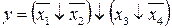
14. 
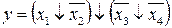
15. 
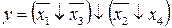
16. 
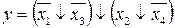
17. 
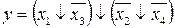
18. 
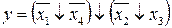
19. 
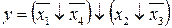
20. 
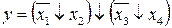
21. 
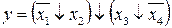
22. 
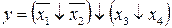
23. 
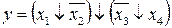
24. 
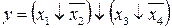
25. 
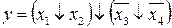
26. 
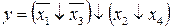
27. 
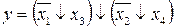
28. 
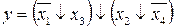
29. 
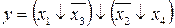
30. 
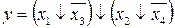
31. 
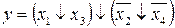
32. 
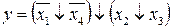
33. 
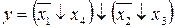
34. 
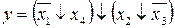
35. 
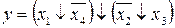
36. 
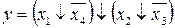
37. 
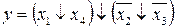
38. 
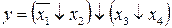
Задача 4. Построить таблицу истинности и логическую схему.
1. 
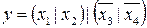
2. 
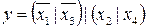
3. 
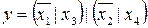
4. 
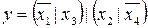
5. 
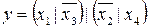
6. 
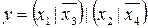
7. 
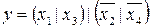
8. 
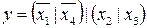
9. 
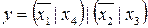
10. 
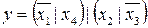
11. 
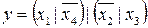
12. 
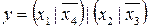
13. 
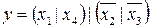
14. 
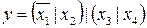
15. 
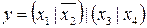
16. 
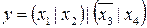
17. 
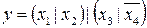
18. 
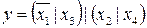
19. 
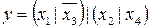
20. 
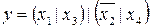
21. 
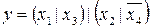
22. 
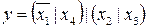
23. 
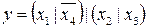
24. 
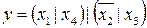
25. 
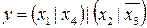
26. 
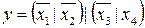
27. 
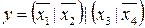
28. 
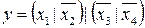
29. 
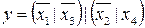
30. 
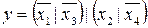
31. 
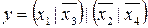
32. 
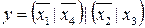
33. 
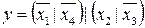
34. 
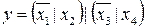
35. 
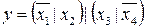
36. 
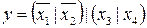
37. 
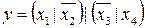
38. 
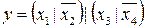
Переход между базисами
Дизъюнктивная нормальная форма(ДНФ) — это нормальная форма, в которой булева формула имеет вид дизъюнкции конъюнкций литералов. Любая булева формула может быть приведена к ДНФ.
Совершенная дизъюнктивная нормальная форма (СДНФ)— это такая ДНФ, которая удовлетворяет трём условиям:
· в ней нет одинаковых элементарных конъюнкций;
· в каждой конъюнкции нет одинаковых пропозициональных букв;
· каждая элементарная конъюнкция содержит каждую пропозициональную букву из входящих в данную ДНФ пропозициональных букв, причём в одинаковом порядке.
Для любой выполнимой функции алгебры логики существует своя СДНФ, причём единственная.
Конъюнктивная нормальная форма (КНФ) — это нормальная форма, в которой булева формула имеет вид конъюнкции дизъюнкций литералов. Конъюнктивная нормальная форма удобна для автоматического доказательства теорем. Любая булева формула может быть приведена к КНФ.
Совершенная конъюнктивная нормальная форма (СКНФ) — это такая КНФ, которая удовлетворяет трём условиям:
· в ней нет одинаковых элементарных дизъюнкций;
· в каждой дизъюнкции нет одинаковых пропозициональных переменных;
· каждая элементарная дизъюнкция содержит каждую пропозициональную букву из входящих в данную КНФ пропозициональных букв.
Для перехода между базисами используются законы де Моргана:
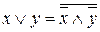, (1)
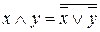. (2)
Выполнив инверсию выражений (1) и (2), получим:
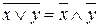, (3)
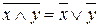. (4)
Также для перехода потребуются формулы Пирса и Шеффера:
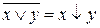, (5)
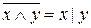. (6)
Выполнив инверсию выражений (5) и (6), получим:
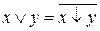, (7)
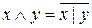. (8)
Задача 5. Задано выражение в совершенной дизъюнктивной нормальной форме:
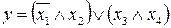. (9)
Требуется перейти к базису Пирса.
Решение.
В базисе Пирса отсутствует операция логического умножения, поэтому с помощью выражения (2) заменим конъюнкцию на дизъюнкцию внутри скобок выражения (9). Получим:
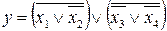. (10)
Внутри скобок выражения (10) применим выражение (5). Получим:
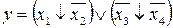. (11)
Применив к выражению (11) операцию (7), получим ответ:
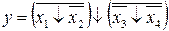. (12)
Замечание. В полученном выражении (12) скобки раскрывать нельзя.
Задача 6. Задано выражение в совершенной дизъюнктивной нормальной форме:
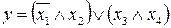. (13)
Требуется перейти к базису Шеффера.
Решение.
В базисе Шеффера отсутствует операция логического сложения, поэтому с помощью выражения (1) заменим дизъюнкцию на конъюнкцию между скобок выражения (13). Получим:
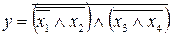. (14)
Внутри скобок выражения (14) применим выражение (6). Получим:
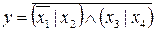. (15)
Применив к выражению (15) операцию (8), получим ответ:
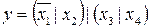. (16)
Замечание. В полученном выражении (16) скобки раскрывать нельзя.
Варианты заданий для задач № 5 и № 6:
1. 
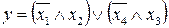
2. 
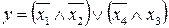
3. 
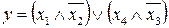
4. 
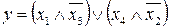
5. 
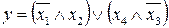
6. 
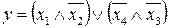
7. 
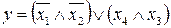
8. 
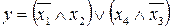
9.
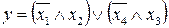
10.
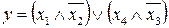
11. 
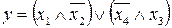
12. 
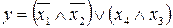
13. 
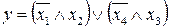
14.
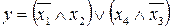
15. 
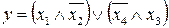
16. 
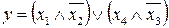
17. 
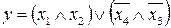
18. 
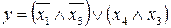
19. 
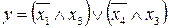
20. 
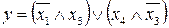
21. 
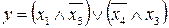
22. 
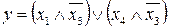
23.
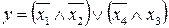
24. 
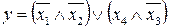
25. 
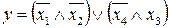
26.
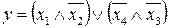
27.
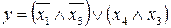
28.
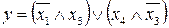
29.
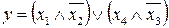
30.
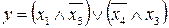
31.
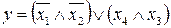
32.
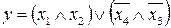
33.
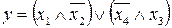
34.
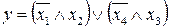
35.
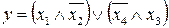
36.
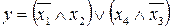
37.
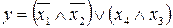
38.
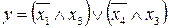
Задача 7. Задано выражение в совершенной конъюнктивной нормальной форме:
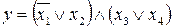. (17)
Требуется перейти к базису Шеффера.
Решение.
В базисе Шеффера отсутствует операция логического сложения, поэтому с помощью выражения (1) заменим дизъюнкцию на конъюнкцию внутри скобок выражения (17). Получим:
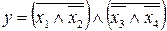. (17)
Внутри скобок выражения (17) применим выражение (6). Получим:
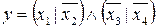. (18)
Применив к выражению (18) операцию (8), получим ответ:
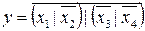. (19)
Замечание. В полученном выражении (19) скобки раскрывать нельзя.
Задача 8. Задано выражение в совершенной конъюнктивной нормальной форме:
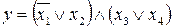. (20)
Требуется перейти к базису Пирса.
Решение.
В базисе Пирса отсутствует операция логического умножения, поэтому с помощью выражения (2) заменим конъюнкцию на дизъюнкцию между скобками выражения (20). Получим:
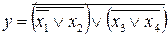. (21)
Внутри скобок выражения (21) применим выражение (5). Получим:
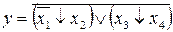. (22)
Применив к выражению (22) операцию (5), получим ответ:
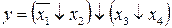. (23)
Замечание. В полученном выражении (23) скобки раскрывать нельзя.
Варианты заданий для задач № 7 и № 8:
1.
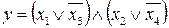
2.
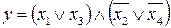
3.
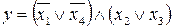
4.
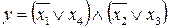
5.
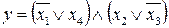
6.
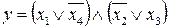
7.
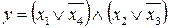
8.
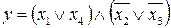
9.
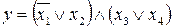
10.
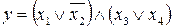
11.
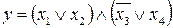
12.
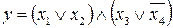
13.
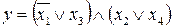
14.
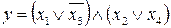
15.
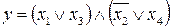
16.
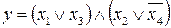
17.
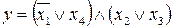
18.
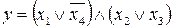
19.
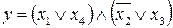
20.
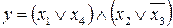
21.
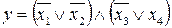
22.
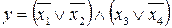
23.
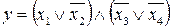
24.
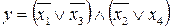
25.
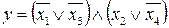
26.
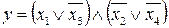
27.
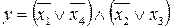
28.
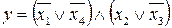
29.
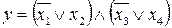
30.
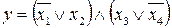
31.
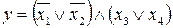
32.
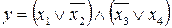
33.
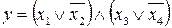
34.
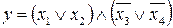
35.
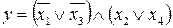
36.
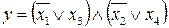
37.
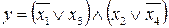
38.