Методы математических доказательств

МАТЕРИАЛЫ ДЛЯ СРС

СРС 1

Изучение материала по теме «Введение. Математическая логика в системе современного образования» по учебнику: Игошин В. И. Математическая логика и теория алгоритмов.- М., Академия, 2004, с. 6-14.

Форма отчётности: конспект.

СРС 2

Выполнение семестрового задания № 1 (по вариантам).

СРСП 1

СРСП 1

СРСП 2

СРСП 2

СРСП 3

СРСП 3

СРСП 4

СРСП 4

СРСП 5

СРСП 5

СРСП 6

СРСП 6

№ зад.

1

2

3

4

5

6

7

8

9

10

11

12

№ вар.

1.14 б

1.18 к

1.26 б

1.58 б

2.1 в

2.2 к

2.12 к

2.15 б

1.35 б

1.40 к

3.29

3.55

1.14 в

1.18 и

1.26 в

1.58 в

2.1 г

2.2 и

2.12 и

2.15 в

1.35 в

1.40 и

3.30

3.56

1.14 г

1.18 з

1.26 г

1.58 г

2.1 д

2.2 з

2.12 з

2.15 г

1.35 г

1.40 з

3.31

3.58

1.14 д

1.18 ж

1.26 д

1.58 д

2.1 е

2.2 ж

2.12 ж

2.15 д

1.35 д

1.40 ж

3.33

3.59

1.14 е

1.18 е

1.26 е

1.58 е

2.1 ж

2.2 е

2.12 е

2.15 е

1.35 е

1.40 е

3.34

3.60

1.14 ж

1.18 д

1.26 ж

1.58 ж

2.1 з

2.2 д

2.12 д

2.15 ж

1.35 ж

1.40 д

3.37

3.61

1.14 з

1.18 г

1.26 з

1.58 з

2.1 и

2.2 г

2.12 г

2.15 з

1.35 з

1.40 г

3.38

3.55

1.14 и

1.18 в

1.26 и

1.58 и

2.1 к

2.2 в

2.12 в

2.15 и

1.35 и

1.40 в

3.39

3.56

1.14 к

1.18 б

1.26 к

1.58 к

2.2 к

2.1 в

2.12 б

2.15 к

1.35 к

1.40 б

3.40

3.58

1.15 б

1.17 к

1.27 б

1.59 б

2.2 и

2.1 г

2.11 к

2.16 б

1.36 б

1.39 к

3.41

3.59

1.15 в

1.17 и

1.27 в

1.59 в

2.2 з

2.1 д

2.11 и

2.16 в

1.36 в

1.39 и

3.42

3.60

1.15 г

1.17 з

1.27 г

1.59 г

2.2 ж

2.1 е

2.11 з

2.16 г

1.36 г

1.39 з

3.43

3.61

1.15 д

1.17 ж

1.27 д

1.59 д

2.2 е

2.1 ж

2.11 ж

2.16 д

1.36 д

1.39 ж

3.29

3.55

1.15 е

1.17 е

1.27 е

1.59 е

2.2 д

2.1 з

2.11 е

2.16 е

1.36 е

1.39 е

3.30

3.56

1.15 ж

1.17 д

1.27 ж

1.59 ж

2.2 г

2.1 и

2.11 д

2.16 ж

1.36 ж

1.39 д

3.31

3.58

1.15 з

1.17 г

1.27 з

1.59 з

2.2 в

2.1 к

2.11 г

2.16 з

1.36 з

1.39 г

3.33

3.59

1.15 и

1.17 в

1.27 и

1.59 и

2.1 в

2.2 к

2.11 в

2.16 и

1.36 и

1.39 в

3.34

3.60

1.15 к

1.17 б

1.27 к

1.59 к

2.1 г

2.2 и

2.11 б

2.16 к

1.36 к

1.39 б

3.37

3.61

1.14 б

1.16 к

1.26 б

1.58 б

2.1 д

2.2 з

2.11 к

2.15 б

1.38 б

1.39 к

3.38

3.55

1.14 в

1.16 и

1.26 в

1.58 в

2.1 е

2.2 ж

2.11 и

2.15 в

1.38 в

1.39 и

3.39

3.56

1.14 г

1.16 з

1.26 г

1.58 г

2.1 ж

2.2 е

2.11 з

2.15 г

1.38 г

1.39 з

3.40

3.58

1.14 д

1.16 ж

1.26 д

1.58 д

2.1 з

2.2 д

2.11 ж

2.15 д

1.38 д

1.39 ж

3.41

3.59

1.14 е

1.16 е

1.26 е

1.58 е

2.1 и

2.2 г

2.11 е

2.15 е

1.38 е

1.39 е

3.42

3.60

1.14 ж

1.16 д

1.26 ж

1.58 ж

2.1 к

2.2 в

2.11 д

2.15 ж

1.38 ж

1.39 д

3.43

3.61

1.14 з

1.16 г

1.26 з

1.58 з

2.2 к

2.1 в

2.11 г

2.15 з

1.38 з

1.39 г

3.29

3.55

1.14 и

1.16 в

1.26 и

1.58 и

2.2 и

2.1 г

2.11 в

2.15 и

1.38 и

1.39 в

3.30

3.56

1.14 б

1.18 к

1.26 б

1.58 б

2.1 в

2.2 к

2.12 к

2.15 б

1.35 б

1.40 к

3.29

3.55

1.14 в

1.18 и

1.26 в

1.58 в

2.1 г

2.2 и

2.12 и

2.15 в

1.35 в

1.40 и

3.30

3.56

1.14 г

1.18 з

1.26 г

1.58 г

2.1 д

2.2 з

2.12 з

2.15 г

1.35 г

1.40 з

3.31

3.58

1.14 д

1.18 ж

1.26 д

1.58 д

2.1 е

2.2 ж

2.12 ж

2.15 д

1.35 д

1.40 ж

3.33

3.59

балл

0,5

0,5

0,5

0,5

0,5

0,5

0,5

0,5

0,5

0,5

0,5

0,5

Задания по учебнику: Игошин В. И. Задачи и упражнения по математической логике и теории алгоритмов.- М., Академия, 2005.

Форма отчётности: семестровое задание необходимо сдавать в отдельных тетрадях в сроки, указываемые преподавателем для каждого задания.

СРС 3

Изучение материала по теме «Приложение АВ к логико-математической практике: строение и виды теорем, методы математических доказательств; нахождение всех следствий из посылок, посылок для следствий, недостающей посылки в рассуждении».

Приложение АВ к логико-математической практике

Строение и виды теорем

В большинстве случаев математические предложения формулируются в виде импликативного высказывания.

а) 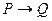(прямая теорема)

Пример.Если диагонали параллелограмма взаимно перпендикулярны, то этот параллелограмм ромб.

б) 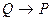(обратное предложение)

Примечание.Обратное предложение может и не быть теоремой.

в) 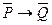(противоположное предложение)

г) 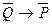(контрапозитивное предложение)

Примечание.Известно, что 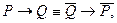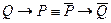(по закону контрапозиции). Поэтому, если 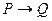- теорема, то и контрапозитивное предложение 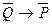тоже будет теоремой. Аналогично, если будет доказано, что обратное предложение 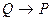является теоремой, то и противоположное предложение 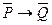также будет теоремой, или наоборот. Если же будет доказано, что обратное предложение 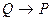не является теоремой, то и противоположное предложение 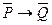также не будет теоремой, или наоборот.

Примечание.Но зачастую формулировки теорем имеют более сложную структуру. Рассмотрим некоторые из них.

I.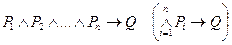

Пример 1.а) Если в параллелограмме диагонали взаимно перпендикулярны и равны, то этот параллелограмм является квадратом.

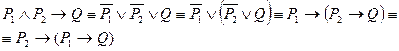
Таким образом, данная теорема имеет три равносильные формы.

Для каждой из них можно образовать по одному обратному предложению:

1)

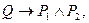
2) ,

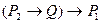3)

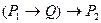
кроме этого, обратив импликации во второй и третьей формах, стоящие в «скобках» получим еще два обратных предложения:

4)

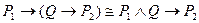
5)

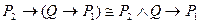
Примечание.Полученные пять форм не равносильны и не все из них являются верными предложениями. В дальнейшем в качестве обратных предложений мы будем рассматривать только предложения, имеющие формы-1,4,5.

Произведя конрапозицию форм (1,4,5), получим предложения противоположные к данной теореме:

1)

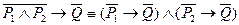
2)

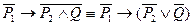
3)

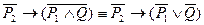
Произведя контрапозицию исходной теоремы, получим одно контрапозитивное предложение:

1)

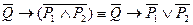
II. .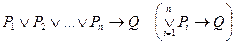

,

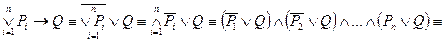
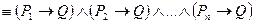то есть в этом случае прямая теорема распадается на n теорем

.

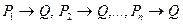Пример 2.

Р₁ – диагонали параллелограмма перпендикулярны,

Р₂ - диагональ является биссектрисой угла,

Q - параллелограмм является ромбом.

а) 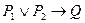- прямая теорема.

б) 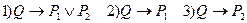(три неравносильных обратных предложения).

в) 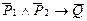- противоположное предложение.

г) 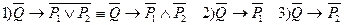- три неравносильных контрапозитивных предложения.

Примечание.Можно рассмотреть и другие структуры теорем.

При формулировках теорем используются термины: необходимо и достаточно.

Если предложение, сформулированное в виде импликации 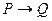, является теоремой, то

а) Р – достаточное условие для Q,

б) Q – необходимое условие для Р.

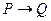		Р по отношению к Q	Q по отношению к P
		не достаточно и не необходимо	не необходимо и не достаточно
		не достаточно, но необходимо	не необходимо, но достаточно
		достаточно, но не необходимо	необходимо, но не достаточно
		достаточно и необходимо	необходимо и достаточно

Пример 3.

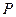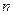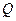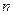: « - чётное число», : «3 - чётное число».

Найти каково 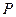по отношению к 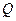и 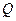по отношению к ?

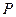Найдём значения высказываний:

1) 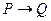: «Если 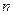чётное число, то 3 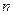тоже чётное число»

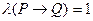
2) : «Если 3 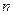чётное число, то 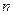чётное число»

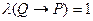
Следовательно, 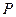достаточное и необходимое условие для ;

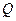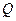необходимое и достаточное условие для .

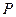Пример 4.

Р - многоугольник правильный,

Q - вокруг многоугольника можно описать окружность.

1) Предложение 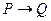- является теоремой, тогда

а) Р достаточное условие для Q.

б) Q необходимое условие для Р.

2) Предложение 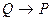- не является теоремой, тогда

а) Q не достаточное условие для Р.

б) Р не необходимое условие для Q.

Таким образом:

а) Правильность многоугольника достаточное, но не необходимое условие, для того чтобы около него можно было описать окружность.

б) Возможность описать окружность необходимое, но недостаточное условие, для того чтобы многоугольник был правильным.

Методы математических доказательств