Средние величины. Общая характеристика и правила выведения

Средние величины позволяют получить обобщённую хар-ристику качественно однородных совокупностей по колич-ному признаку.

В отличие от относительных величин средние величины выражаются именованными цифрами, а не отвлечёнными показателями.

Основные правила расчёта средних величин:

1. средняя величина рассчитывается на основе массовых статистических данных;

2. необходимо использовать качественно однородные совокупности;

3. среднюю величину статистическую следует отличать от средней математической величины.

Средняя статистическая величина отличается от средней математической, её нельзя отличать от закономерности, это только её проявление.

Виды средних величин:

1. 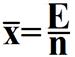средняя арифметическая

х – средняя арифметическая

Ʃ – сумма величин

n – частота

2. средняя арифметическая взвешенная

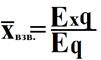х_взв – средняя арифметическая взвешенная

Ʃ ∙q – сумма произведения вариантов

Ʃ q – сумма весов

3. средняя арифметическая интервального ряда – сначала определяем середину интервала, затем рассчитываем по формуле арифметической взвешенной

х_инт.

4. средние структурные величины или квазис средней – можно посмотреть или увидеть:

1) мода – это вариант значений, ктрому соответ-ет наибольшая частота или вес;

2) медиана – это серединное значение или центральный вариант ранжированного вариационного ряда.

Средняя арифметическая.

Средняя арифметическая является наиболее распространенным видом средних величин. Она бывает двух видов: средняя арифметическая простая и средняя арифметическая взвешенная.

Средняя арифметическая простая есть частное отделение суммы вели­чин на их число. Например, требуется определить среднемесячную нагрузку следователя РОВД одного из сельских районов Томской области, если извест­но, что один го них за месяц рассмотрел 12 уголовных дел, 2-ой — 10, 3-й - 18, а 4-й - 8.

Средняя арифметическая простая:

Средняя арифметическая взвешенная применяется в тех случаях, когда значения признаков (в нашем примере 12, 10, 18 и 8) повторяются по не сколько раз. Например, в городском ОВД по 12 уголовных дел в месяц рассматривает не один, а 10 следователей, по 10 уголовных дел - 18 следователей по 18 дел - 5 и по 8 дел - 7 следователей. Тогда:

Иными словами, средняя арифметическая взвешенная есть частное отде­ления суммы произведений каждого значения признака на число единиц имеющих это значение, - на общее число единиц совокупности.

Иногда значение признака выражается не в виде определенного числа, а виде интервала «от - до».

В этом случае необходимо сначала определить центры интервалов (как среднюю арифметическую интервала), а потом производить расчеты способом изложенным выше.

Мода и медиана.

Мода и медиана - это наиболее простые виды средних величин, которые не требуют специальных расчетов.

Модой называется величина (численное значение признака), которая наиболее часто встречается в изучаемой совокупности. Например, 1000 осуж­денных за изнасилование распределились по возрасту следующим образом:

от 14 до 20 лет - 650 чел. от 20 до 30 лет - 250 чел. от 30 до 40 лет - 80 чел. свыше 40 лет - 20 чел.

В изучаемой совокупности наиболее часто (650) встречается численное значение признака «от 14 до 20 лет». Это и будет мода, которая не требует ка­ких-либо специальных расчетов. Глядя на распределение осужденных по воз­расту, каждый может достаточно определенно сказать, что изнасилование чаще всего совершается лицами в возрасте от 14 до 20 лет.

Медианой называется показатель, который расположен в центре так на­зываемого ранжированного ряда.

Так, например, средний рост солдат, построенных по росту в одну колон­ну из 15 человек, будет рост восьмого солдата, т.к. именно он находится в цен­тре ранжированного ряда. Это и будет являться медианой роста.

Или, например, за массовые беспорядки (ст.212 УК ч.1) предусматривает­ся наказание в виде лишения свободы на срок от 4-х до 10 лет. Ранжированный ряд, построенный по возрастанию предусмотренной законом санкции с интер­валом о I год, будетвыглядеть следующим образом: 4, 5, 6, 7, 8, 9, 10. Медианой санкции в данном случае будет срок наказания 7 лет, т.к. именно этот по­казатель расположен в центре ранжированного ряда.