Дифференциальные и интегральные законы распределения случайной величины

Случайная величина наилучшим и исчерпывающим образом характеризуется в теории вероятностей законом ее распределения. Этот закон устанавливает связь между возможными значениями случайной величины и соответствующими этим значениям вероятностям их появления. Существует две формы описания закона распределения случайной величины - дифференциальная и интегральная. Причем, в метрологии в основном используется дифференциальная форма - закон распределения плотности вероятностей случайной величины.

Дифференциальный закон распределения характеризуется плотностью распределения вероятностей f(x) случайной величины х. Вероятность Р попадания случайной величины в интервал от х₁ до х₂ при этом дается формулой:

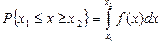
Графически эта вероятность представляет собой отношение площади под кривой f(x) в интервале от х₁ до х₂ к общей площади, ограниченной всей кривой распределения. Как правило, площадь под всей кривой распределения вероятностей нормируют на единицу.

В данном случае представлено распределение непрерывной случайной величины. Кроме них существуют и дискретные случайные величины, принимающие ряд определенных значений, которые можно пронумеровать.

Интегральный закон распределения случайной величины представляет собой функцию F(x), определяемую формулой

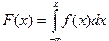
Вероятность, что случайная величина будет меньше х₁ дается значением функции F(х) при х = х₁ :

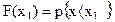Хотя закон распределения случайных величин является их полной вероятностной характеристикой, нахождение этого закона является довольно трудной задачей и требует проведения многочисленных измерений. Поэтому на практике для описания свойств случайной величины используют различные числовые характеристики распределений. К ним относятся моменты случайных величин: начальные и центральные, которые представляют собой некоторые средние значения. При этом если усредняются величины, отсчитываемые от начала координат, то моменты называются начальными, а если от центра распределения – то центральными.

Начальный момент k-го порядка определяется формулой:

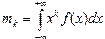
Наибольший практический интерес представляет начальный момент первого порядка - математическое ожидание случайной величины m₁ (k=1):

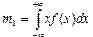
Математическое ожидание определяет положение центра группирования случайной величины, вокруг которого наблюдается ее рассеяние. Экспериментальной оценкой математического ожидания при многократных измерениях является среднее арифметическое значение измеряемой величины.

Центральный момент k-го порядка определяется формулой:

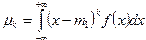
Особую роль играет центральный момент второго порядка. Он называется дисперсией D случайной величины и характеризует рассеяние отдельных ее значений:

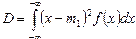
На практике чаще используется среднее квадратическое отклонение σ (СКО) случайной величины, определяемое формулой:

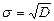
При более подробном изучении распределений случайной величины используются моменты более высоких порядков. Так, любой нечетный центральный момент характеризует асимметрию распределения. Например, третий момент используют для нахождения коэффициента асимметрии кривой распределения относительно математического ожидания. Четвертый центральный момент характеризует остроту вершины кривой распределения.