Исчисление предикатов как модель представления знаний

Рассмотрим сеологизм оСократе

Все люди смертны известно что Сократ человек, следовательно Сократ смертен

a-все люди смертны

в – сократ человек

с- сократ смертен

недоказуемо что

a&b -> c

Возможности исчисления высказываний не хватает для математического доказательства таких выражений которые с точки зрения здравого смысла истинны

Высказывание рассматривает любое утверждение как целое, не выделяя его структуру

Чтобы правильно доказать что сократ смертен, надо доказать что есть множество людей со свойством смертности и что сократ принадлежит ему

Пердикат это логическая функция, в записи которой проявлена структура утверждений

P(x,…,z)

- Общий вид

В записи предиката выделяются две части , первая – предикатный символ

Вторая часть – множество Термов , всякие разные понятия которые связываются при помощи предикатного символа

Предикаты различают по количеству термов, есть одноместные, n – местные предикаты

Утверждение грибы в лесу, В – связывает два объекта

Порядок термов очень важен, определив однажды предикат и зафиксировав в нем порядок термов во всей теории надо придерживаться этого порядка ибо от него зависит символ

Если предикатный символ (в двухместном) вставить между термов будет осмысленная фраза

Термы бывают разных видов

1) Индивидные константы (предметные константы) ИК (ПК) - имена собственные объектов

Обозначают конкретный экземпляр

Обозначаются маленькими буквами с начала алфавита или маленькими буквами с индексом

2) Предметные переменные – имена множеств однотипных объектов, люди, столы

Большие буквы внутри записи, либо символы из конца алфавита без индексов

3) Функциональные константы – единичные объекты порожденные от другого объекта при помощи какой то операции

Варить(картошка₁) на выходе будет вареная картошка

Функциональные константы – не предикаты, у неё множество значений – множество других объектов

Записываются как обычные функции f(x₁)

4) Функциональные переменные – множество функциональных констант, выход – новая переменная обозначающая новое множество

Как определить истинности предиката

Если возьмем константу

Четное(2)

Скажем что число два четное, истинность высказывания = 1

Если все термы – ИК,ФК то истинность предиката определяется легко

Если переменная

Х – числа

Р – быть четным

Р(х)

Для истинности не хватает каких то ограничений, если соблюдаются – истина

Квантры

Квантр всеобщности

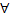
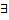
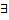! - квантр единичного существования

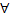х Р(х) = 0

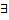хР(х)=1

Формально исчисление предикатов – расширение исчисления высказываний

Рассмотрим какие существуют операции по преобразованию кванторов

С появлением исчисления предикатов появилась еще нормальная форма

Еще есть предваренная нормальная форма

Формула исчисления предикатов имеет вид ПНФ если присутствуют кванторы всеобщности которые вынесены в левую часть формулы и образуют префикс

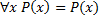можно отбросить префикс и работать уже с матрицей

Второй вариант когда есть только квантр существования

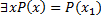
Если квантров существования несколько они равноправны, это принципиально ничего не меняет

Если они разные и их несколько то порядок важен.

Х – множество объектов

Н(х) – быть человеком

М(х) –быть смертным

С₁ – Сократ

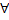x(H(x)->M(x))

H(c₁)

?(M(c₁)

В форме ПНФ надо представить

1) (не(Н(х) или М(х))

2) Н(с₁)

3) Не М(с₁)

4)

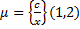
ПОдставновка в выражениях где надо провести резолюцию называется наиболее общим унификатором

Подставлять можно константы вместо переменных, переменные вместо констант нельзя, переменные вместо переменных, одну константу вместо другой

М(с₁)

5) (4,3)

Рассмотрим более сложный пример

Про робота и детали

Имеются предикаты

Просв(Д)

Обт(Д)

В(Д,П)

У(Д,Р)

Обтачивает(Р,Д)