Семейство распределений Стьюдента
Эти законы описывают плотность распределения вероятности среднего арифметического, вычисленного по выборке из n случайных отсчетов нормально распределенной генеральной совокупности. Распределения Стьюдента нашли широкое применение при статистической обработке результатов многократных измерений. Их вид зависит от числа отсчетов n, по которым находится среднее арифметическое значение, поэтому и говорят о семействе законов.
В центрированном и нормированном виде они описываются формулой
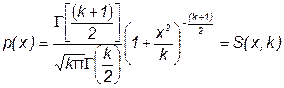 ,
,
где k – число степеней свободы, зависящее от числа n усредняющих отсчетов: k=n-1. При увеличении k распределение Стьюдента переходит в распределение Гаусса.
Для нормированных распределений Стьюдента с k>4 справедливы следующие соотношения:
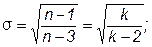
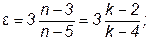
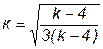
Распределения Стьюдента имеют ряд особенностей:
– при n≤3 их СКО становится равным бесконечности, т.е. дисперсионная оценка ширины разброса не работает (перестает существовать);
– классический аппарат моментов для оценки формы и ширины распределения Стьюдента с малым числом степеней свободы оказывается не работоспособным, и их ширина и форма могут быть оценены лишь с использованием доверительных и энтропийных оценок. Этим распределение Стьюдента резко отличается от других распределений.
Разновидностью распределения Стьюдента является распределение Коши. Оно важно тем, что ему подчиняется распределение отношения двух нормально распределенных центрированных случайных величин. Распределение Коши – это предельное распределение семейства законов Стьюдента с минимально возможным числом степеней свободы, равным k=1:
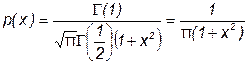 .
.
В общем виде (не нормированном и не центрированном) распределение Коши имеет вид:
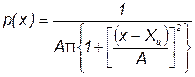 ,
,
где А, Хц – параметры распределения.
Свойства распределения Коши резко отличаются от свойств экспоненциальных распределений, а именно:
– дисперсия и СКО не существуют, так как определяющий их интеграл расходится. Они будут бесконечно увеличиваться при росте числа экспериментальных данных. Оценка ширины распределения может быть произведена только на основе теории информации;
– оценка центра в виде среднего арифметического для распределения Коши неправомочна, так как ее рассеяние равно бесконечности:
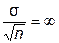 ;
;
– математическое ожидание не существует;
– для определения Хц необходимо использовать медиану;
– эксцесс равен бесконечности, а контрэксцесс равен нулю;
– энтропийное значение погрешности равно 2πA.
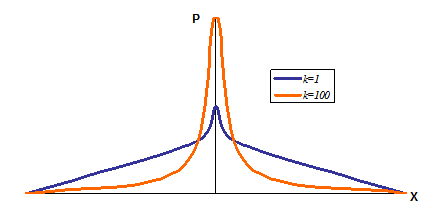
Рис. 9.
