Точечные оценки истинного значения и среднеквадратического отклонения

Мы подошли к решению вопроса о том, как на основании полученной в эксперименте группы результатов наблюдений оценить истинное значение, т.е. найти результат измерений, как оценить его точность, т.е. меру его приближения к истинному значению.

Эта задача является частным случаем статистической задачи нахождения оценок параметров функции распределения случайной величины на основании выборки - ряда значений, принимаемых этой величиной в n независимых опытах. Оцениваемыми параметрами являются математическое ожидание и среднеквадратическое отклонение, поскольку только они входят в выражение для дифференциальных функций всех трех рассмотренных выше распределений. В уравнениях (25) и (30) для нормального распределения и распределения Лапласа эти параметры входят явно, а в уравнения (23) и (24) для равномерного распределения - не явно, поскольку

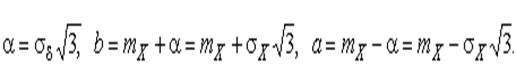
Оценку 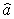параметра а назовем точечной, если она выражается одним числом. Любая точечная оценка, вычисленная на основании опытных данных, является их функцией и поэтому сама должна представлять собой случайную величину с распределением, зави-сящим от распределения исходной случайной величины, в том числе от самого оцениваемого параметра и от числа опытов n.

К точечным оценкам предъявляется ряд требований, определяющих их пригодность для описания самих параметров.

1. Оценка называется состоятельной, если при увеличении числа наблюдений она приближается (сходится по вероятности) к значению оцениваемого параметра.

2. Оценка называется несмещенной, если ее математическое ожидание равно оцениваемому параметру.

3. Оценка называется эффективной, если ее дисперсия меньше дисперсии любой другой оценки данного параметра.

На практике не всегда удается удовлетворить одновременно все эти требования, однако выбору оценки должен предшествовать ее критический анализ со всех перечисленных выше точек зрения.

Существует несколько методов определения оценок. Наиболее распространен метод максимального правдоподобия, теоретически обоснованный математиком Р. Фишером. Идея метода заключается в следующем. Вся получаемая в результате многократных наблюдений информация об истинном значении измеряемой величины и рассеивании результатов сосредоточена в ряде наблюдений 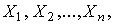, где n - число наблюдений. Их можно рассматривать как n независимых случайных величин с одной и той же дифференциальной функцией распределения 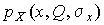. 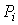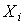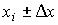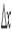Вероятность получения в эксперименте некоторого результата , лежащего в интервале , где - некоторая малая величина, равна соответствующему элементу вероятности .

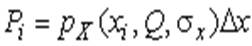Независимость результатов наблюдений позволяет найти априорную вероятность появления одновременно всех экспериментальных данных, т.е. всего ряда наблюдений 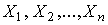как произведение этих вероятностей:

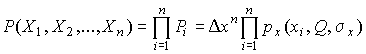
Если рассматривать Q и 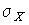как неизвестные параметры распределения, то, подставляя различные значения Q и 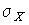в эту формулу, мы будем получать различные значения вероятности 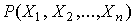при каждом фиксированном ряде наблюдений 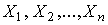. При некоторых значениях 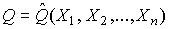и 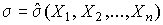вероятность получения экспериментальных данных 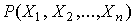достигает наибольшего значения. В соответствии с методом максимального правдоподобия именно эти значения и принимаются в качестве точечных оценок истинного значения и среднеквадратического отклонения результатов наблюдений.

Таким образом, метод максимального правдоподобия сводится к отысканию таких оценок 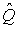и 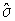, при которых функция правдо-подобия

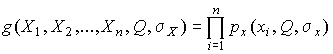(31)

достигает наибольшего значения. Постоянный сомножитель 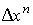не оказывает влияния на решение и поэтому может быть отброшен. Полученные оценк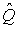и и 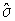истинного значения и среднеквадратического отклонения называются оценками максимального правдоподобия.

Для упрощения вычислений иногда бывает удобнее пользоваться логарифмической функцией правдоподобия

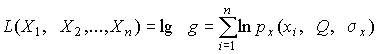(32)

Если наибольшее значение функции правдоподобия совпадает с максимальным значением, то оценки получаются из системы уравнений

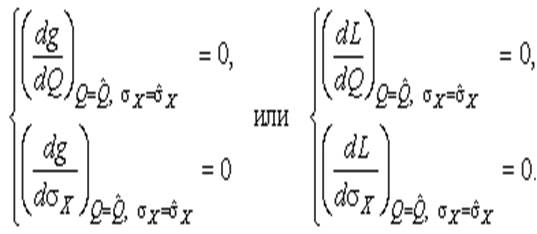(33)

В противном случае необходимо более подробное исследование функции правдоподобия.

Далее определим оценки максимального правдоподобия для трех распределений случайных погрешностей, представленных в предыдущей главе.

1. Результаты наблюдений распределены нормально. В этом случае

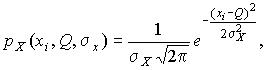
a логарифмическая функция правдоподобия в соответствии с (32)

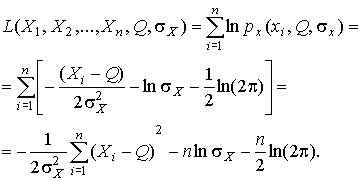
Система уравнений (33) приводится к виду

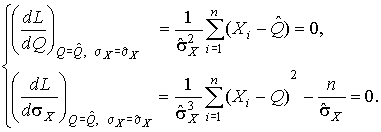
Из первого уравнения получаем выражение для оценки истинного значения 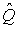, а из второго - оценку среднеквадратического отклонения :

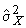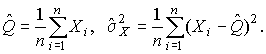
Таким образом, при нормальном распределении случайных погрешностей оценкой максимального правдоподобия для истинного значения является среднее арифметическое из результатов отдельных наблюдений, а оценкой дисперсии - среднее из квадратов отклонений результатов наблюдений от среднего арифметического.

2. Результаты наблюдений распределены по закону Лапласа

.

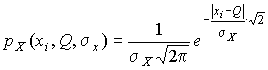Логарифмическая функция правдоподобия не является дифференцируемой по Q, поэтому приходится прибегать к численным методам, функция правдоподобия достигает наибольшего значения, когда выражение 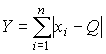принимает наименьшее значение. Поэтому задача об отыскании оценки ис-тинного значения сводится к определению такого значения 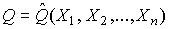, сумма модулей отклонений результатов наблюдений от которого является наименьшей. Задача решается методом последовательных приближений, причем в качестве первого приближения можно принять среднее арифметическое из полученных результатов.

3. В условиях равномерного распределения погрешностей

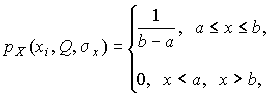
причем 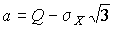и .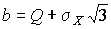

Решение задачи нахождения оценки максимального правдоподобия для равномерного распределения погрешностей проводим численными методами, в результате чего получаем:

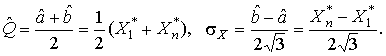
Основное достоинство оценок максимального правдоподобия в том, что они являются асимптотически (при 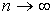) несмещенными; асимптотически эффективными и асимптотически нормально распределенными.

Если 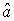- оценка максимального правдоподобия для параметра а, то при достаточно большом числе n наблюдений (практически уже при n>20-25) эту оценку можно считать нормально распределенной с математическим ожиданием 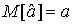и дисперсией 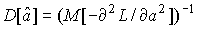при любом распределении результатов наблюдений.

Для наиболее часто встречающегося на практике нормального распределения случайных погрешностей оценки максимального правдоподобия имеются особые обозначения.

Оценкой истинного значения является среднее арифметическое 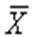из результатов отдельных наблюдений ,

.

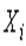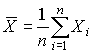Вторая производная от логарифмической функции преобразования равна 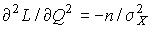, поэтому дисперсия среднего арифметического в n раз меньше дисперсии 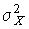результатов наблюдений, т. е.

.

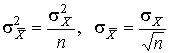Оценка дисперсии результатов наблюдений при малом n является немного смещенной, поэтому точечную оценку дисперсии принято определять как

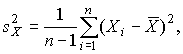
а оценку среднеквадратического отклонения результатов наблюдений как

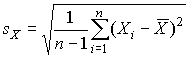
Дисперсия оценки 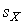среднеквадратического отклонения составляет

.

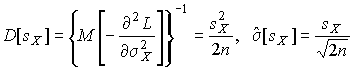Последнее соотношение показывает, что относительная погрешность определения среднеквадратического отклонения (в %) по результатам обработки ряда наблюдений достаточно велика:

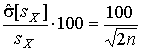
и даже при 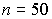достигает 10%. Для надежного суждения о точности эту погрешность следует увеличить еще минимум в два раза.

С помощью полученных оценок итог измерений можно записать в виде

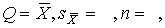
что уже позволяет сделать некоторые выводы относительно точности проведенных измерений.

Наряду с методом максимального правдоподобия при определении точечных оценок широко используется метод наименьших квадратов. В соответствии с этим методом среди некоторого класса оценок выбирают ту, которая обладает наименьшей дисперсией, т. е. наиболее эффективную оценку. Легко заметить, что среди всех линейных оценок истинного значения вида 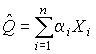, где 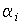- некоторые постоянные, именно среднее арифметическое 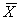обращает в минимум дисперсию 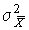. Поэтому для случая нормально распределенных случайных погрешностей оценки, получаемые методом наименьших квадратов, совпадают с оценками максимального правдоподобия.