Основные правила построения модели
Математическую модель изображают в виде графа состояний. Элементы графа:
- кружки (вершины графа 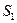 ,
, 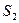 ,…,
,…, 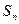 ) – возможные состояния системы
) – возможные состояния системы 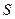 , возникающие при отказах элементов;
, возникающие при отказах элементов;
- стрелки – возможные направления переходов из одного состояния 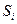 в другое
в другое 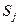 .
.
Над/под стрелками указываются интенсивности переходов.
Примеры диаграмм графа представлен на рис. 2.16.
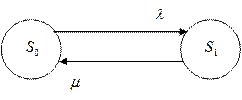 а) а) | 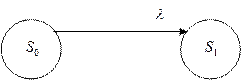 б) б) |
Рисунок 2.16 – Примеры диаграмм графа состояний системы с восстановлением («восстанавливаемый элемент») (а) и системы без восстановления («невосстанавливаемый элемент») (б)
На рис 2.16 введены следующие обозначения:
- 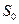 – работоспособное состояние;
– работоспособное состояние;
- 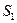 – состояние отказа.
– состояние отказа.
Граф состояний отражает конечное (дискретное) число возможных состояний системы 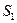 ,
, 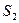 ,…,
,…, 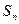 . Каждая из вершин графа соответствует одному из состояний.
. Каждая из вершин графа соответствует одному из состояний.
Для описания случайного процесса перехода состояний (отказ/ восстановление) применяют вероятности состояний
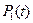 ,
, 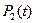 , … ,
, … , 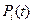 , … ,
, … , 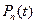 ,
,
где 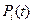 – вероятность нахождения системы в момент
– вероятность нахождения системы в момент 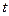 в
в 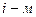 состоянии,
состоянии, 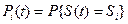 .
.
Очевидно, что для любого 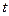
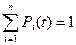 (2.42)
(2.42)
По графу состояний (рис. 2.17) составляется система обыкновенных дифференциальных уравнений первого порядка (уравнений Колмогорова-Чепмена), имеющих вид
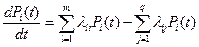 . (2.43)
. (2.43)
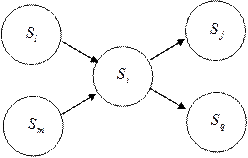
Рисунок 2.17 – Диаграмма графа состояний
В общем случае, интенсивности потоков 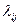 и
и 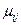 могут зависеть от времени
могут зависеть от времени 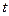 .
.
При составлении дифференциальных уравнений пользуются простым мнемоническим правилом:
а) в левой части – производная по времени 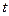 от
от 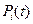 ;
;
б) число членов в правой части равно числу стрелок, соединяющих рассматриваемое состояние с другими состояниями;
в) каждый член правой части равен произведению интенсивности перехода на вероятность того состояния, из которого выходит стрелка;
г) знак произведения положителен, если стрелка входит в рассматриваемое состояние, и отрицателен, если стрелка выходит из него.
Чтобы решить систему дифференциальных уравнений для вероятностей состояний 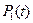 ,
, 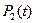 , … ,
, … , 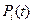 , … ,
, … , 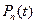 необходимо задать начальное значение вероятностей
необходимо задать начальное значение вероятностей 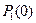 ,
, 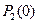 , … ,
, … , 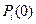 , … ,
, … , 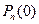 , при
, при 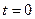 , сумма которых равна единице:
, сумма которых равна единице:
Если в начальный момент 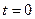 состояние системы известно, например,
состояние системы известно, например, 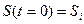 , то
, то 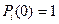 , а остальные равны нулю
, а остальные равны нулю
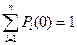 .
.
