Тема I.3. Равносильность формул. Законы логики высказываний

Тема I.4. Аксиоматический метод. Исчисление высказываний.

Тема I.5. Нормальные формы формул логики высказываний.

Занятие 3.

Тема II.1. Понятие булевой функции.

Тема II.2. Равенство функций. Основные законы булевой алгебры.

Занятие 4.

Тема II.2. Равенство функций. Основные законы булевой алгебры (продолжение)

Тема II.3. Совершенная дизъюнктивная нормальная форма. Совершенная конъюктивная нормальная форма.

Занятие 5.

Тема III.1. Основные понятия теории графов.

Занятие 6.

Тема III.2. Приложение теории графов к решению задач.

Занятие 7.

Тема III.2. Приложение теории графов к решению задач (продолжение).

Занятие 8.

Тема III.2. Приложение теории графов к решению задач (продолжение).

Занятие 9.

Тема IV.1. Теория множеств.

Занятие 10.

Тема IV.2. Случайные события и их вероятности.

Занятие 11.

Тема IV.3. Случайные величины.

Тема IV.4. Основные законы распределения. Предельные теоремы.

Занятие 12.

Тема IV.5. Методы принятия решений.

Занятие 13.

Контрольная работа.

Раздел I. Аксиоматический метод.

Тема I.1 Высказывания. Логические операции и их таблицы истинности.

Примеры истинных высказываний, ложных. Примеры предложений не являющихся высказываниями. Обозначения истинных и ложных высказываний.

Элементарные высказывания, составные (сложные) высказывания.

Логические операции: отрицание, конъюнкция, дизъюнкция, импликация. Эквивалентность. Таблицы истинности для основных логических операций.

Пример выполнения упражнений:

Укажите, какие из следующих предложений являются высказываниями, установите истинность простых высказываний. В сложных высказываниях выделите конъюнкцию и дизъюнкцию, установите истинность. Возьмите первые два высказывания и сформулируйте отрицание, конъюнкцию и дизъюнкцию.

1.

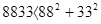
2.

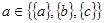
3.

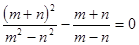
4. «Треугольник называется равносторонним, если его стороны равны между собой».

5. «Антонио Вивальди – итальянский композитор».

6. «Марс и Венера – планеты Солнечной системы».

7. 10<9+1 тогда и только тогда, когда 9<8+1

8. «Христофор Колумб открыл Америку или Африку».

9. Если -3<-1, то 3²=6.

10. 15 делится на 5 и на 2.

Литература: [1], [2], [3], [4], [5].

Тема I.2. Формулы логики высказываний.

Логические константы, логические переменные высказывательные, пропозициональные. Формулы и подформулы формул логики высказываний. Примеры формул сложных высказываний (получение сложного высказывания из простых и наоборот). Процесс перевода суждений естественного языка на язык логики высказываний.

Тождественно-истинные формулы (тавтология), тождественно-ложные формулы (противоречия), нейтральные формулы.

Таблицы истинности для подформул и формул.

Пример выполнения упражнений:

1. Написать формулу для предложения: «Если взяться за дело с желанием и довести начатое до конца, то результат обеспечен». Построить таблицу истинности данной формулы и проанализировать все возможные сочетания истинных значений.

2. Формулизовать сократовское высказывание: «Если тебе попадется хорошая жена, то будешь счастливым исключением, а если плохая, то будешь философом». Составить таблицу истинности и, проанализировать её, ответить на вопрос, какие жизненные ситуации Сократ полагал нереальными.

Литература: [1], [2], [5].

Тема I.3. Равносильность формул. Законы логики высказываний.

Проверка равносильности двух любых формул с помощью таблицы истинности.

Свойства равносильности формул: рефлексивность, коммутативность, транзитивность.

Законы логики высказываний: законы 0 и 1; закон исключенного третьего, закон противоречия, закон двойного отрицания, законы идемпотентности, законы де Моргана, законы поглощения, законы коммутативности конъюнкции и дизъюнкции, законы дистрибутивности, закон контрапозиции, правила замены логических операций.

Пример: С помощью таблицы истинности проверить, являются ли равносильным формулы F и G:

1.

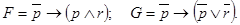
2.

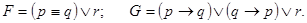
3.

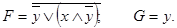
Литература: [1], [2], [5].

Тема I.4. Аксиоматический метод. Исчисление высказываний.

Геометрия Евклида как пример аксиоматического метода. Определение аксиоматического метода.

Правила логического вывода: правило отделение, правило силлогизма, правило равносильной замены, правило подстановки. Корректность правила логического вывода.

Гильбертово исчисление высказываний.

Обратные и противоположные утверждения. Логическое следование. Метод резолюций.

Примеры: 1. Для формулы 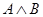логической операции конъюнкции построить равносильную от формулу, содержащую только логические операции отрицания и дизъюнкции.

2. Пусть даны предложения: 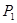: «Если студент подготовился, то он сдаст экзамены»;

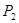: «Студент, провалившийся на экзамене, не подготовился».

Выяснить, имеет ли место следование 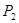и .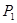

Литература: [1], [2].

Тема I.5. Нормальные формы формул логики высказываний.

Примеры формул, имеющих нормальную форму и не имеющих такую форму. Алгоритм приведения формулы к нормальной форме.

Конъюнктивная нормальная форма (КНФ). Дизъюнктивная нормальная форма (ДНФ).

Примеры: 1. Привести к нормальной форме формулу 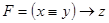, имеющую три логические переменные: x, y, и z.

2. Является ли формула 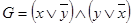конъюктивной нормальной формой.

3. Выяснить, является ли результат решения примера 1. (нормальная форма 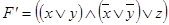, КНФ.

4. Найти ДНФ формулы .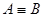

5. Составить формулу логики в нормальной форме по заданной таблице истинности.

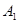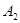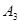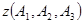Литература: [1].

Раздел II. Основные структуры.

Тема II.1. Понятие булевой функции.

Определение булевой функции. Логические переменные и логические функции. Таблица истинности булевой функции. Булевы функции одной и двух переменных. Соответствие набора двоичных чисел десятичной системе счисления.

Пример: Составить таблицу соответствия набора двоичных чисел десятичной системы счисления для трех логических переменных.

Литература: [1], [2], [5].

Тема II.2. Равенство функций. Основные законы булевой алгебры.

Соседние наборы значений переменных булевой функции. Существенные и фиктивные переменные. Примеры. Равенство булевых функций.

Законы булевой алгебры: законы нуля и единицы; закон исключения третьего, закон противоречия, закон двойного отрицания, законы идемпотентности, законы де Моргана, законы поглощения, законы коммутативности логического умножения и сложения, законы ассоциативности логического умножения и сложения, законы дистрибутивности, закон контрапозиции, правила замены логических операций.

Примеры: 1. Используя логический метод основанный на использовании законов алгебры логики, доказать, что .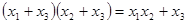

2. Применяя табличный метод доказать один из законов де Моргана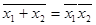

Литература: [1], [2].

Тема II.3. Совершенная дизъюнктивная нормальная форма. Совершенная конъюнктивная нормальная форма.

Понятия правильной (совершенной) дизъюнкции и конъюнкции. Равносильность СДНФ и СКНФ.

Примеры: 1. По данному разложению булевой функции по переменным в нормальной форме построить СДНФ и СКНФ.

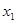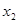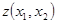2. Зная формулу в СДНФ: 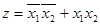, получить СКНФ.

Литература: [1], [2].