Анализ надежности систем при множественных отказах

Рассмотрим метод анализа надежности нагруженных элементов в случае статистически независимых и зависимых (множественных) отказов. Следует заметить, что этот метод может быть применен и в случае других моделей и распределений вероятностей. При разработке этого метода предполагается, что для каждого элемента системы существует некоторая вероятность появления множественных отказов.

Как известно, множественные отказы действительно существуют, и для их учета в соответствующие формулы вводится параметр a. Этот параметр может быть определен на основе опыта эксплуатации резервированных систем или оборудования и представляет собой долю отказов, вызываемых общей причиной. Другими словами, параметр а можно рассматривать как точечную оценку вероятности того, что отказ некоторого элемента относится к числу множественных отказов. При этом можно считать, что интенсивность отказов элемента имеет две взаимоисключающие составляющие, т. е. l=l₁+l₂, где l₁ - постоянная интенсивность статистически независимых отказов элемента, l₂ - интенсивность множественных отказов резервированной системы или элемента. Поскольку a=l₂/l, то l₂= a/ l, и следовательно, l₁ =(1- a)l.

Приведем формулы и зависимости для вероятности безотказной работы, интенсивности отказов и средней наработки на отказ в случае систем с параллельным и последовательным соединением элементов, а также систем с k исправными элементами из п и систем, элементы которых соединены по мостиковой схеме.

Система с параллельным соединением элементов (рис. 4.5.13) - обычная параллельная схема, к которой последовательно подсоединен один элемент. Параллельная часть (I) схемы отображает независимые отказы в любой системе из n элементов, а последовательно соединенный элемент (II) - все множественные отказы системы.

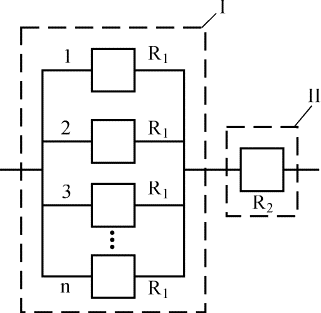
Рис. 4.5.13. Модифицированная система с параллельным соединением одинаковых элементов

Гипотетический элемент, характеризуемый определенной вероятностью появления множественного отказа, последовательно соединен с элементами, которые характеризуются независимыми отказами. Отказ гипотетического последовательно соединенного элемента (т.е. множественный отказ) приводит к отказу всей системы. Предполагается, что все множественные отказы полностью взаимосвязаны. Вероятность безотказной работы такой системы определяется как R_р={1-(1-R₁)ⁿ}R₂, где n - число одинаковых элементов; R₁ - вероятность безотказной работы элементов, обусловленная независимыми отказами; R₂ - вероятность безотказной работы системы, обусловленная множественными отказами.

При постоянных интенсивностях отказов l₁ и l₂ выражение для вероятности безотказной работы принимает вид

R_р(t)={1-(1-e^-(1-a)lt)ⁿ}e^-alt, (4.5.28)
где t - время.

Влияние множественных отказов на надежность системы с параллельным соединением элементов наглядно демонстрируется с помощью рис. 4.5.14 – 4.5.16; при увеличении значения параметра a вероятность безотказной работы такой системы уменьшается.

Параметр a принимает значения от 0 до 1. При a=0 модифицированная параллельная схема ведет себя как обычная параллельная схема, а при a=1 она действует как один элемент, т. е. все отказы системы являются множественными.

Поскольку интенсивность отказов и среднее время наработки на отказ любой системы можно определить с помощью (4.3.7) и формул
,
,
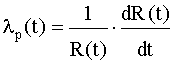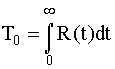с учетом выражения для R_р(t) получаем, что интенсивность отказов (рис. 4.5.17) и средняя наработка на отказ модифицированной системы соответственно равны
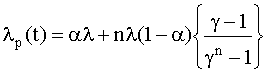, (4.5.29)
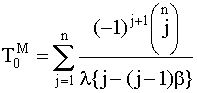, где 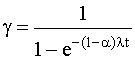. (4.5.30)

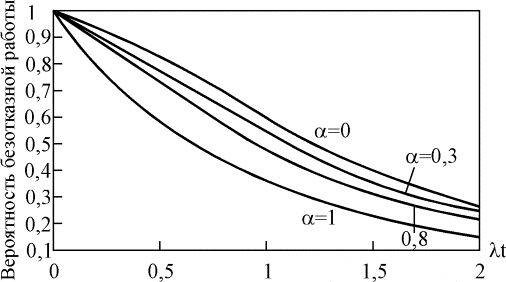
Рис. 4.5.14. Зависимость вероятности безотказной работы системы с параллельным соединением двух элементов от параметра a

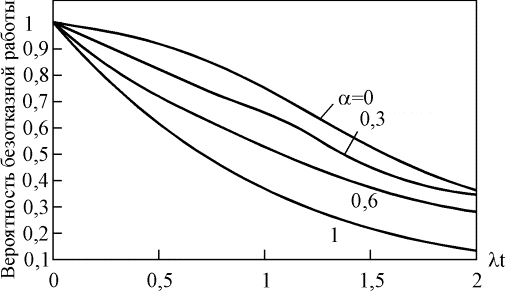
Рис. 4.5.15. Зависимость вероятности безотказной работы системы с параллельным соединением трех элементов от параметра a

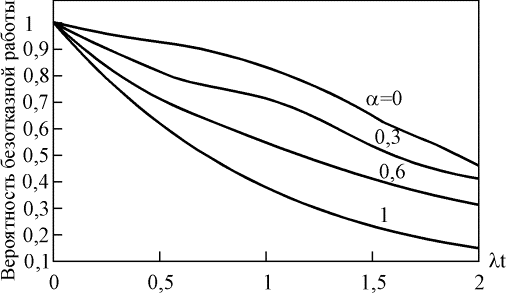
Рис. 4.5.16. Зависимость вероятности безотказной работы системы с параллельным соединением четырех элементов от параметра a

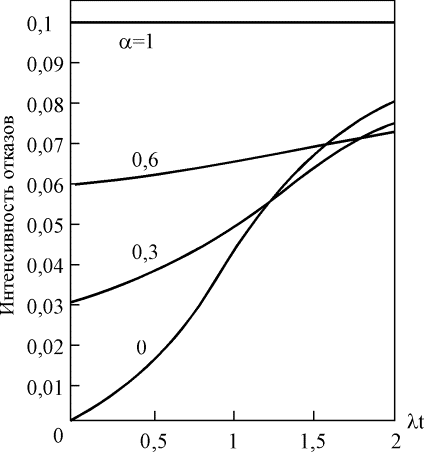
Рис. 4.5.17. Зависимость интенсивности отказов системы с параллельным соединением четырех элементов от параметра a

Пример 4.5.12. Требуется определить вероятность безотказной работы системы, состоящей из двух одинаковых параллельно соединенных элементов, если l=0,001 ч^-1; a=0,071; t=200 ч.

Вероятность безотказной работы системы, состоящей из двух одинаковых параллельно соединенных элементов, для которой характерны множественные отказы, равна 0,95769. Вероятность безотказной работы системы, состоящей из двух параллельно соединенных элементов и характеризуемой только независимыми отказами, равна 0,96714.

Система с k исправными элементами из п одинаковых элементов включает в себя гипотетический элемент, соответствующий множественным отказам и соединенный последовательно с обычной системой типа k из n, для которой характерны независимые отказы. Отказ, отображаемый этим гипотетическим элементом, вызывает отказ всей системы. Вероятность безотказной работы модифицированной системы с k исправными элементами из n можно вычислить по формуле

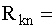
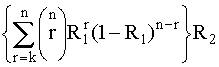, (4.5.31)

где R₁ - вероятность безотказной работы элемента, для которого характерны независимые отказы; R₂ - вероятность безотказной работы системы с k исправными элементами из n, для которой характерны множественные отказы.

При постоянных интенсивностях l₁ и l₂ полученное выражение принимает вид

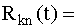
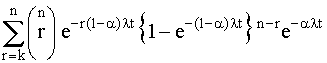. (4.5.32)

Зависимость вероятности безотказной работы от параметра a для систем с двумя исправными элементами из трех и двумя и тремя исправными элементами из четырех показаны на рис. 4.5.18 - 4.5.20. При увеличении параметра a вероятность безотказной работы системы уменьшается на небольшую величину (lt).

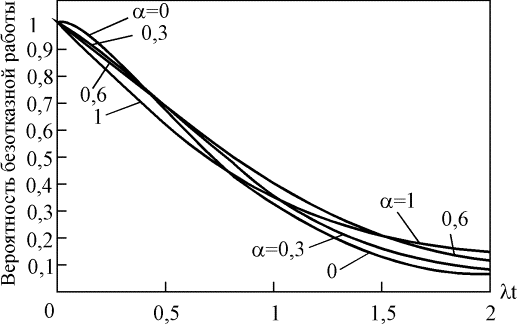
Рис. 4.5.18. Вероятность безотказной работы системы, сохраняющей работоспособность при отказе двух из n элементов

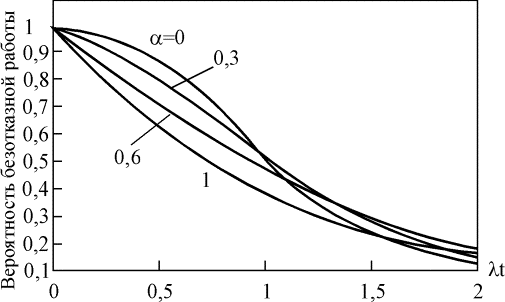
Рис. 4.5.19. Вероятность безотказной работы системы, сохраняющей работоспособность при отказе двух из четырех элементов

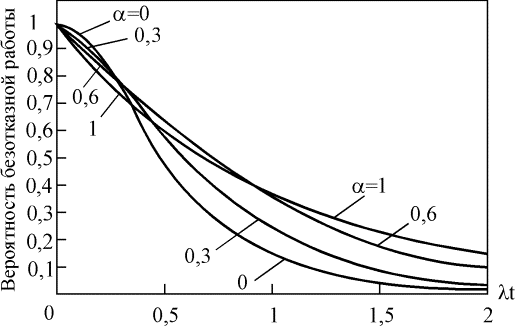
Рис. 4.5.20. Вероятность безотказной работы системы, сохраняющей работоспособность при отказе трех из четырех элементов

Интенсивность отказов системы с k исправными элементами из n и средняя наработка на отказ могут быть определены следующим образом:

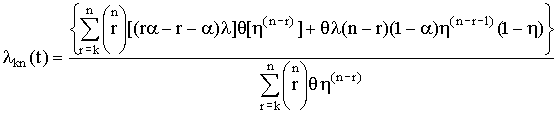, (4.5.33)

где h = {1-e^-(1-b)lt},

q = e^(ra-r-a)lt

и

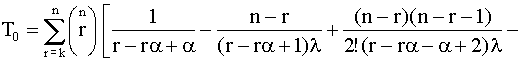
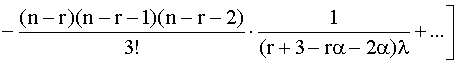. (4.5.34)

Пример 4.5.13. Требуется определить вероятность безотказной работы системы с двумя исправными элементами из трех, если l=0,0005 ч^-1; a=0,3; t=200 ч.

С помощью выражения для R_kn находим, что вероятность безотказной работы системы, в которой происходили множественные отказы, составляет 0,95772. Отметим, что для системы с независимыми отказами эта вероятность равна 0,97455.

Система с параллельно-последовательным соединением элементов соответствует системе, состоящей из одинаковых элементов, для которых характерны независимые отказы, и ряда ветвей, содержащих воображаемые элементы, для которых характерны множественные отказы. Вероятность безотказной работы модифицированной системы с параллельно-последовательным (смешанным) соединением элементов можно определить с помощью формулы R_ps={1-(1- 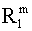)ⁿ}R₂, где m - число одинаковых элементов в ответвлении, n - число одинаковых ответвлений.

При постоянных интенсивностях отказов l₁ и l₂ это выражение принимает вид

R_рs (t) = [1-(1-e^-n(1-a)lt)^m}e^-alt. (4.5.35)

Интенсивность отказов системы с параллельно-последова­тельным соединением элементов и средняя наработка на отказ могут быть определены следующим образом:

l_ps(t)=al+mn(1-a)l 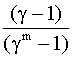, (4.5.36)

где l=1/[1-e^-n(1-g)lt] и

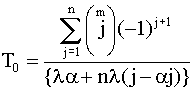. (4.5.37)

Система, элементы которой соединены по мостиковой схеме,соответствует схеме, состоящей из одинаковых элементов, для которых характерны независимые отказы, и последовательно подсоединенного к ним воображаемого элемента, для которого характерны множественные отказы. При множественном отказе гипотетического элемента вся система выходит из строя. Вероятность безотказной работы модифицированной системы с элементами, соединенными по мостиковой схеме, можно вычислить по формуле

R_b={1-2(1-R₁)⁵+5(1-R₁)⁴-2(1-R₁)³-2(1-R₁)²}R₂ (4.5.38)

(здесь R_b - вероятность безотказной работы мостиковой схемы, для которой характерны множественные отказы). Эта формула при постоянных интенсивностях l₁ и l₂ принимает вид

R_b(t)=[1-2(1-e^-At)⁵+5(1- e^-At)⁴-2(1- e^-At)³-2(1- e^-At)²] e^-blt. (4.5.39)

(здесь А=(1-a)l). Зависимость безотказной работы системы R_b(t) для различных параметров a показана на рис. 4.5.21. При малых значениях lt вероятность безотказной работы системы с элементами, соединенными по мостиковой схеме, убывает с увеличением параметра a.

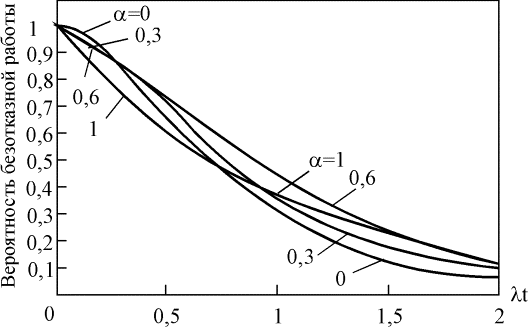
Рис. 4.5.21. Зависимость вероятности безотказной работы системы, элементы которой соединены по мостиковой схеме, от параметра a

Интенсивность отказов рассматриваемой системы и средняя наработка на отказ могут быть определены следующим образом:
l_kn(t)=bl+A(-8p⁵+25p⁴-24p³+4p²+4p)+ 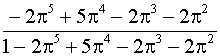, (4.5.40)

где p=(1-e^-At) и

Т₀= 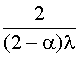+ + 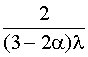+ 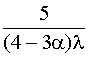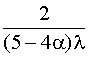. (4.5.41)

Пример 4.5.14. Требуется вычислить вероятность безотказной работы в течение 200 ч для системы с одинаковыми элементами, соединенными по мостиковой схеме, если l=0,0005 ч^-1 и a=0,3.

Используя выражение для R_b(t), находим, что вероятность безотказной работы системы с соединением элементов по мостиковой схеме составляет примерно 0,96; для системы с независимыми отказами (т.е. при a=0) эта вероятность равна 0,984.